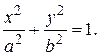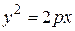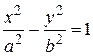Алгоритм решения систем линейных алгебраических

Уравнений с помощью формул Крамера

1. Для матрицы А системы уравнений вычислить ее главный определитель = det A.

2. Последовательно, заменяя каждый столбец матрицы А столбцом свободных членов, получить побочные определители , .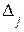

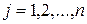3. а) Если 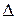≠ 0, то по формулам (4) определить единственное решение системы (1): , , …., .

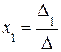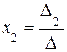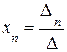б) Если 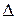=0, а хотя бы один из побочных определителей 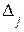≠0, то исходная система (1) несовместна, то есть не имеет решений.

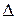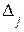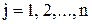в) Если = = 0, , то исходная система (1) имеет бесконечное множество решений.

Пример. Решить систему линейных алгебраических уравнений с помощью формул Крамера

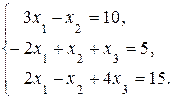
Решение.

1. Матрица А имеет вид: А = 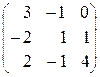, detA = 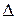=5 ≠ 0,

Следовательно, система имеет единственное решение.

2. Найдем побочные определители системы:

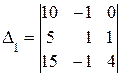=10ּ 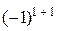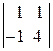+(–1)ּ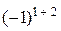 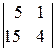=10ּ5+5=55;

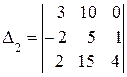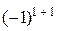
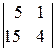=3ּ +10ּ 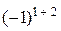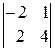=3ּ5–10ּ(–10)=115;

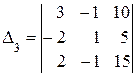=( упростим, сложив первую строку со второй и

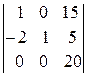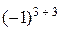
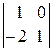третью со второй)= =20 ּ =20.

9. Метод Гаусса решения систем линейных алгебраических уравнений.

Рассмотрим еще один метод решения систем линейных алгебраических уравнений – метод Гаусса, который применим к любой системе линейных алгебраических уравнений. Иногда этот метод называют методом последовательного исключения неизвестных. Заметим, что при использовании этого метода мы также автоматически будем вычислять ранг матрицы системы.

Итак, пусть задана система m линейных алгебраических уравнений с n неизвестными:

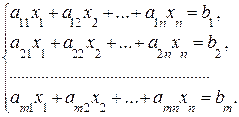(6)

В матричном виде система (6) записывается АХ=В, где А – прямоугольная матрица размера m´n:

А= 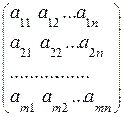, а Х и В – матрицы-столбцы: Х= 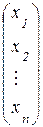, В= .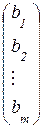

Если в результате преобразований матрицы системы получится треугольная матрица, то система будет иметь вид:

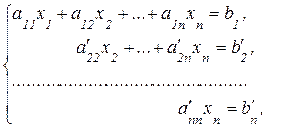
где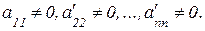

Из последнего уравнения можно найти 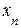, а затем, подставляя найденное 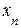в предпоследнее уравнение, найти 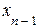и т.д. В итоге будем иметь единственное решение 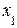, , 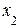…, 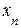. В этом случае ранг матрицы А системы уравнений равен n.

Если в результате преобразований матрицы системы получится трапециевидная матрица, то система примет вид:

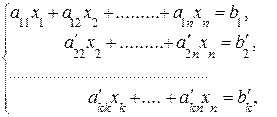
где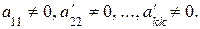

В этом случае k<n, следовательно, система уравнений будет неопределенной, то есть будет иметь бесконечное множество решений, так как она содержит n – k свободных переменных:

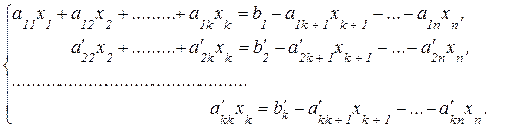
Придавая свободным переменным 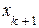, , 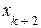…, 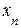произвольные значения, будем иметь каждый раз новое решение исходной системы уравнений, то есть решений будет бесконечное множество. В этом случае ранг матрицы А системы равен k.

Если в результате преобразований получено уравнение, в котором коэффициенты при всех неизвестных равны нулю, а свободный член отличен от нуля, то такая система будет несовместной, то есть не иметь решения.

Следует отметить, что треугольная или трапециевидная форма системы уравнений получалась ввиду предположения, что коэффициенты 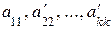отличны от нуля. Если же какой-либо из этих коэффициентов равен нулю, то система уравнений приобретет треугольную или трапециевидную форму лишь после надлежащего изменения нумерации неизвестных.

В заключение отметим, что метод Гаусса применяется и для однородных систем линейных алгебраических уравнений. В этом случае, если получаем треугольный вид системы уравнений, то она будет иметь единственное (нулевое) решение 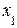= = 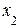…= =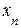0, если же получаем трапециевидный вид системы, то будем иметь бесконечное множество решений.

При решении системы линейных алгебраических уравнений методом Гаусса удобно выписать расширенную матрицу системы и все преобразования выполнять над строками и столбцами расширенной матрицы.

Рассмотрим примеры решения систем линейных алгебраических уравнений методом Гаусса.

Пример 1.

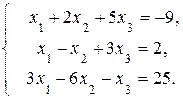
Решение.

Выпишем расширенную матрицу системы:

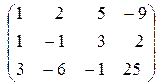~ (не меняя первую строку, вычтем из второй

строки первую, из третьей вычтем первую строку, умноженную

на 3) ~ 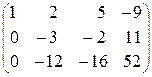~ (первую и вторую строки не меняем,

а из третьей вычтем вторую, умноженную на 4) ~ .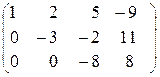

Получили матрицу А треугольного вида, причем на диагонали элементы отличны от нуля. Следовательно, ранг матрицы А равен 3, ранг расширенной матрицы также равен 3, и по теореме Кронекера-Капелли исходная система совместна, причем имеет единственное решение. Получим это решение.

Согласно последней матрице исходную систему можно записать в виде:

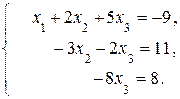
Из последнего уравнения имеем, что 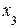= –1. Подставляя 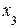во второе уравнение, получим 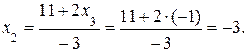Подставляя 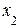и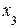

в первое уравнение, получим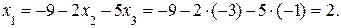

Ответ: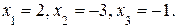

Пример 2.

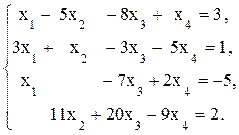
Решение.

Выпишем расширенную матрицу системы:

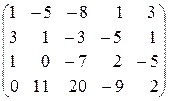~ (первую и четвертую строки не меняем, из

второй строки вычтем первую, умноженную на 3, из третьей строки вычтем

первую) ~ 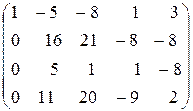~ (первую и вторую строки не меняем, из третьей строки вычтем вторую, умноженную на 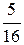, а из четвертой вычтем вторую, умноженную на ) ~ ~

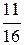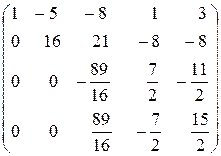~ (первую, вторую и третью строки не меняем, к четвертой строке

прибавим третью) ~ .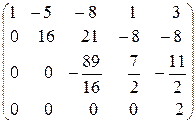

В итоге получили трапециевидную матрицу А. Следовательно, если бы последняя строка расширенной матрицы была нулевой, то исходная система уравнений имела бы бесконечное множество решений.

Так как она дает уравнение 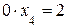, которое не имеет решения, то исходная система является несовместной, то есть не имеет решений.

10. Скалярные и векторные величины. Линейные операции с векторами.

Вектором называется направленный отрезок 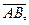где точка А – начало вектора, точка В – конец вектора. Если начало и конец вектора в явном виде не указаны, то вектор будем обозначать 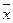и т. д.

Вектор, у которого начало и конец совпадают, называется нулевым вектором и обозначается .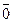

Длиной (модулем) вектора называется длина его направленного отрезка и обозначается , .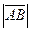

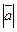Вектор, длина которого равна единице, называется единичным или ортом.

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.

Два вектора и 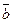называются равными 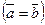, если они коллинеарны, имеют одинаковую длину и одинаковое направление.

Свободный вектор – это вектор, который можно переносить параллельно самому себе в любую точку пространства (плоскости).

Произведением вектора на число 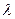называется вектор 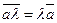, длина которого 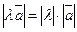; направление совпадает с направлением вектора , если 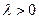, и противоположно ему, если .

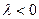Суммой двух векторов 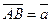и 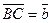называется вектор 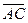(рис. 1) и обозначается .

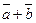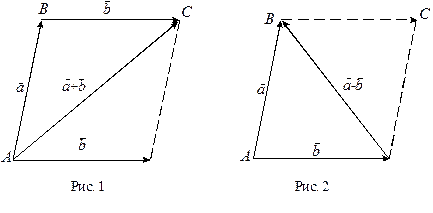
Разностью двух векторов и 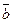называется вектор 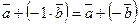и обозначается 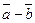(рис. 2).

Векторы, лежащие в одной плоскости или на параллельных плоскостях, называются компланарными.

Декартовой прямоугольной системой координат в пространстве (прямо-угольной) называется совокупность трех упорядоченных взаимно перпендикулярных осей координат ОХ, ОY, OZ с общим началом в точке О. Орты координатных осей ОХ, ОY, ОZ обозначают 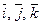соответственно. Векторы 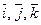образуют декартовый прямоугольный базис в пространстве.

11. Понятие базиса на плоскости и в пространстве. Ортонормированные базисы на плоскости и в пространстве. Координаты вектора в базисе.

Базисом на плоскости 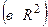называется упорядоченная пара любых некомпланарных векторов этой плоскости.

Базисом в пространстве 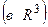называется упорядоченная тройка любых некомпланарных векторов.

Векторы 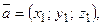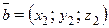, 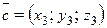в пространстве образуют базис тогда и только тогда, когда определитель матрицы, составленной из их координат,

не равен нулю: .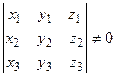

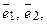Если – базис на плоскости, то любой вектор этой плоскости единственным образом представляется в виде линейной комбинации векторов т. е. .

Числа 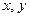называют координатами вектора в базисе 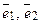и записывают .

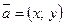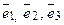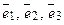Если – базис в пространстве, то любой вектор единственным обра-зом представляется в виде линейной комбинации векторов , т. е. 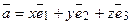. Числа 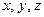называют координатами вектора в базисе 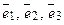и записывают .

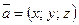Координатами точки М в заданной системе координат называют координаты ее радиус-вектора 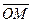. В этом случае пишут 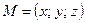или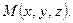

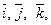Любой вектор в пространстве единственным образом представляется в виде линейной комбинации векторов т. е. 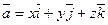. Числа 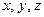называют декартовыми прямоугольными координатами вектора и записывают .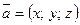

Линейные операции над векторами в координатной форме: пусть 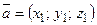, , 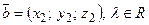тогда , .

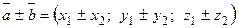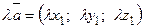Длина вектора вычисляется по формуле

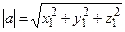. (2.1)

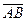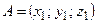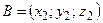Если вектор задан координатами точек и , то

.

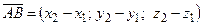12. Скалярное произведение. Координатная форма скалярного произведения.

Скалярным произведением двух векторов и 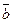называется число, равное произведению длин этих векторов на косинус угла 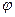между ними:

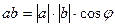. (2.3)

Скалярное произведение в координатной форме:

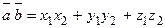. (2.4)

Из определения скалярного произведения следует, что

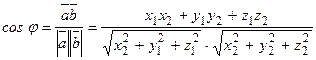. (2.5)

По значению косинуса находится угол между ненулевыми векторам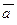и и .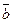

Ненулевые векторы и 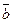перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю:

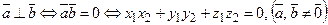. (2.6)

Ненулевые векторы и 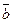коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны:

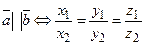. (2.7)

Проекция вектора на вектор 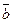вычисляется по формуле 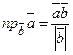. (2.8)

Примеры

1. Даны координаты точек , .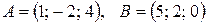

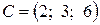Вычислить длину вектора

.

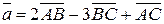Р е ш е н и е. Найдем координаты векторов 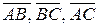по формуле (2.2):

.

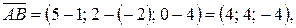
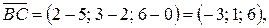
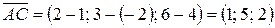Найдем координаты вектора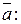

= .

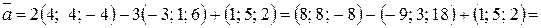
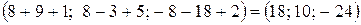Тогда длина вектора 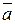находится по формуле (2.1):

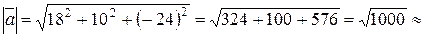31,6.

13. Векторное произведение. Координатная форма векторного произведения.

Векторным произведением векторов и 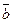называется вектор, обозначаемы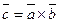й или 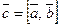, удовлетворяющий условиям:

1) 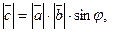где 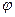– угол между векторами и 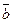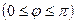; (2.9)

2) , ;

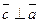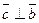3) упорядоченная тройка векторов 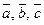– правая, т. е. если смотреть из конца вектора 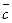, то кратчайший поворот от вектора к вектору 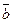осуществляется против хода часовой стрелки (в противном случае тройка называется левой).

Если хотя бы один из векторов и 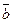нулевой, то полагают .

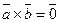Векторное произведение в координатной форме:

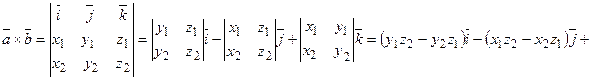
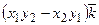+ . (2.10)

Ненулевые векторы и 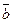коллинерны тогда и только тогда, когда их векторное произведение равняется нулевому вектору; 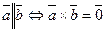. (2.11)

Геометрический смысл векторного произведения: длина вектора 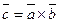векторного произведения векторов и 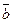численно равняется площади параллелограмма, построенного на векторах и 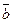, приведенных к общему началу.

14. Смешанное произведение. Координатная форма смешанного произведения.

Смешанным произведением трех векторов 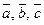называется число, обозначаемое 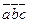или 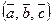и равное скалярному произведению вектора 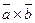на вектор : .

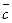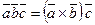Смешанное произведение векторов 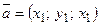, , 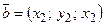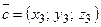в координатной форме:

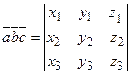. (2.12)

Ненулевые векторы 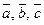компланарны тогда и только тогда, когда их смешанное произведение равняется нулю .

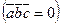Геометрический смысл смешанного произведения: смешанное произведение трех векторов 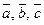численно равняется объему параллелепипеда, построенного на векторах 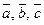(приведенных к общему началу), взятому со знаком «+», если тройка 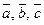– правая, и взятому со знаком «–», если тройка 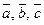– левая.

15. Уравнение прямой (на плоскости), уравнение плоскости, заданных точкой и нормальным вектором.

Будем предполагать, что на плоскости задана прямоугольная система координат .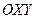

Нормальным вектором прямой называется любой ненулевой вектор, перпендикулярный этой прямой.

Уравнение прямой, заданной точкой 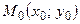и нормальным вектором :

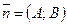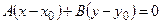. (3.1)

Общее уравнение прямой:

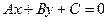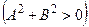, . (3.2)

Частные случаи общего уравнения прямой:

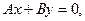
1) 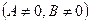– прямая проходит через начало координат;

2) 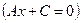, 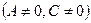– прямая параллельна оси ;

3) 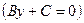, 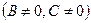– прямая параллельна оси ОХ;

4) 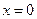– уравнение оси ОY;

5) 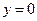– уравнение оси ОХ.

16. Общее уравнение плоскости, общие уравнения прямой в пространстве, общее уравнение прямой на плоскости.

17. Уравнение прямой (на плоскости), уравнение плоскости в отрезках.

18. Уравнения прямой на плоскости и в пространстве, проходящей через 2 заданные точки.

19. Уравнение прямой на плоскости и в пространстве, заданной точкой и направляющим вектором.

20. Уравнение плоскости, проходящей через 3 заданные точки.

21. Расстояние от точки до прямой и от точки до плоскости.

22. Эллипс и его основные свойства.

Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек F₁ и F₂ этой плоскости, называемых фокусами эллипса, есть заданная постоянная величина, равная 2а, а > 0, большая, чем расстояние между фокусами 2с, с > 0.

Пусть фокусы эллипса лежат на оси Х, причем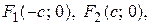
т. е. 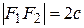– межфокусное расстояние эллипса.

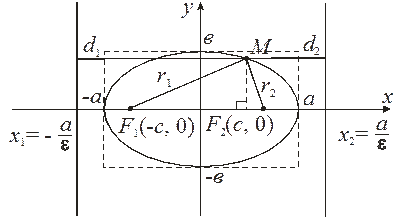
Пусть 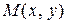– произвольная точка эллипса. Величины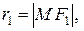 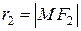называются фокальными радиусами точки М эллипса.

По определению эллипса: r₁ + r₂ = 2a, а > c. Из прямоугольных треугольников, по теореме Пифагора, имеем:

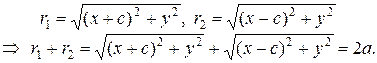(2)

Умножим (2) на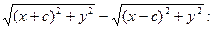

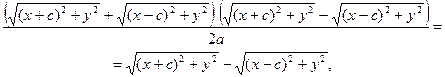
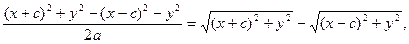
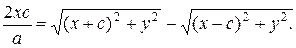(3)

Сложим уравнения (2) и (3):

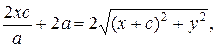
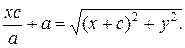(4)

Возведем (4) в квадрат:

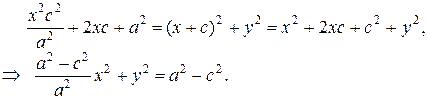
Пусть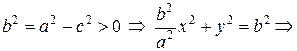

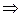(5)

(5) – каноническое уравнение эллипса с центром в начале координат. Соответственно, уравнение

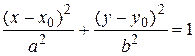
– каноническое уравнение эллипса с центром в точке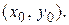

Числа а и 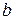называются соответственно большой и малой полуосями эллипса. Заметим, что а > 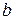, если а < 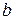, то фокусы эллипса будут на оси Оу, если а = 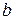, то эллипс превращается в окружность.

Точки 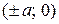, 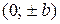называются вершинами эллипса. Отметим, что эллипс целиком расположен внутри прямоугольника: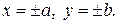

Так как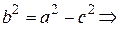

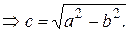(6)

Эксцентриситетом эллипса e называют отношение межфокусного расстояния 2с к длине большой оси 2а.

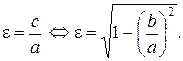(7)

Следовательно, 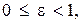причем 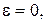когда 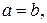т. е. имеем окружность.

При 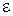стремящемся к 1 эллипс становится более вытянутым вдоль оси Ох.

Выразим фокальные радиусы точки 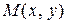через эксцентриситет. Из (4):

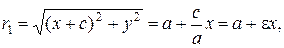(8)

Из (3):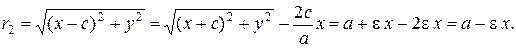

Значит, подставив координаты точки эллипса в уравнения (8), получаем фокальные радиусы точки М.

Прямые 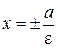называются директрисами эллипса.

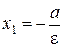– левая директриса,

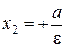– правая директриса.

Заметим, что директрисы эллипса обладают следующим важным свойством:

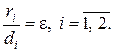(9)

т. е. отношение расстояния r_i от любой точки эллипса до фокуса к расстоянию d_i от нее до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса.

23. Парабола и ее основные свойства.

Параболой называется множество точек плоскости, равноудаленных от данной точки F этой плоскости, называемой фокусом параболы, и данной прямой, называемой ее директрисой.

Построим уравнение параболы.

Пусть ось Оx проходит через фокус F параболы и перпендикулярен директрисе, а ось Оу проходит посередине между фокусом и директрисой. Обозначим через p – расстояние между фокусом и директрисой. Тогда 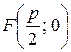, а уравнение директрисы .

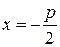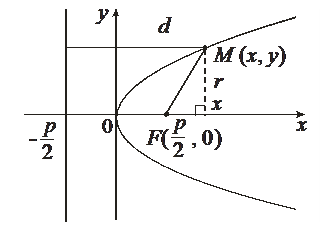Число p – называется фокальным параметромпараболы.

Пусть 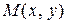– произвольная точка параболы. Пусть 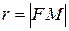– фокальный радиус точки M. d – расстояние от точки М до директрисы. Тогда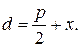

По определению параболы 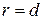. Следовательно

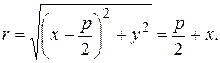
Возведем это уравнение в квадрат

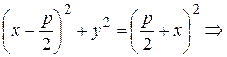
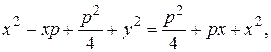
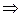(20)

– каноническое уравнение параболы, симметричной относительно оси Оx и проходящей через начало координат.

Точка (0; 0) – вершина параболы.

Если р > 0 (р > 0 ), то парабола (20) расположена правее (левее) оси Оу.

Так как для параболы 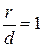, а для эллипса и гиперболы 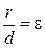, то, следовательно, эксцентриситет параболы равен 1 (e = 1).

Заметим, что парабола, симметричная относительно Оу и проходящая через начало координат, определяется уравнением

х² = 2q y (21)

Фокус этой параболы находится в точке 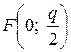. Уравнение ее директрисы 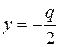. Фокальный радиус ее точки М(х, у) выражается формулой .

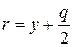Если q > 0 (q < 0), то ветви параболы (21) расположены выше (ниже) оси Ох.

24. Гипербола и ее основные свойства.

Гиперболой называется множество точек плоскости, для каждой из которых модуль разности расстояний от которых до двух данных точек 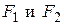той же плоскости, называемых фокусами гиперболы, есть заданная постоянная величина 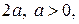меньшая, чем расстояние между фокусами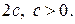

Пусть фокусы гиперболы лежат на оси Ох, причем 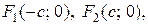т. е. 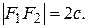Заметим, что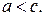

Пусть 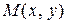– произвольная точка гиперболы. Как и ранее, 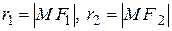– фокальные радиусыточки М.

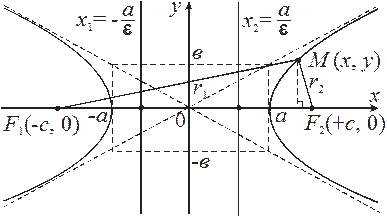
По определению гиперболы:

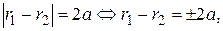
где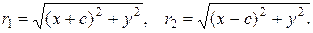

Следовательно,

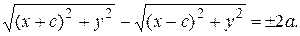(10)

Умножим (10) на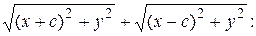

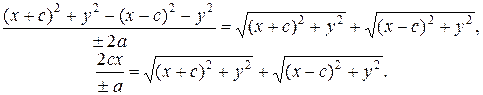(11)

Сложим уравнения (10) и (11):

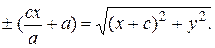(12)

Возведем (12) в квадрат:

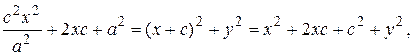
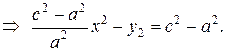
Пусть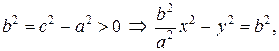

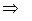(13)

(13) – каноническое уравнение гиперболы с центром в начале координат. Соответственно, уравнение

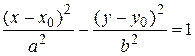
– каноническое уравнение гиперболы с центром в точке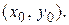

Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Гипербола с равными полуосями (a=b) называется равносторонней, ее каноническое уравнение имеет вид:

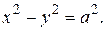
Точки 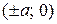называются вершинами гиперболы.

Заметим, что если уравнение гиперболы имеет вид

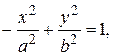(14)

то фокусы гиперболы находятся на оси Оу, а ветви гиперболы будут направлены не влево и вправо, а вверх и вниз.

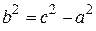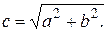Так как , то (15)