Скалярное произведение векторов. Угол между векторами
Скалярным произведением двух векторов 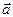 и
и 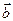 называется произведение модулей этих векторов на косинус угла между ними.
называется произведение модулей этих векторов на косинус угла между ними.
Обозначение: 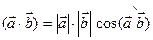
Особые случаи:
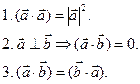
Если векторы 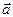 и
и 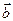 заданы своими координатами:
заданы своими координатами: 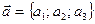 и
и 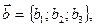 то скалярное произведение вычисляется по формуле
то скалярное произведение вычисляется по формуле 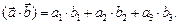
Угол между векторами выражается следующим образом: 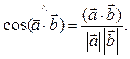
В координатной форме 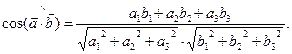
Пример 3.
Найти угол между векторами 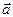 и
и 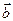 , если
, если 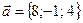 и
и 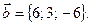
Решение:
Обозначим: 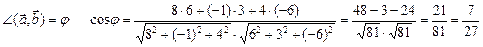 .
.
Ответ: 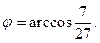
Введение в теорию пределов функций
Определение: число А называется пределом функции y = f(x) при 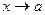 , если для любого числа
, если для любого числа 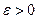 , существует
, существует 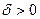 такое, что при
такое, что при 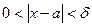 выполняется неравенство
выполняется неравенство 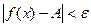 .
.
Обозначение: 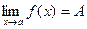 .
.
Основные свойства пределов:
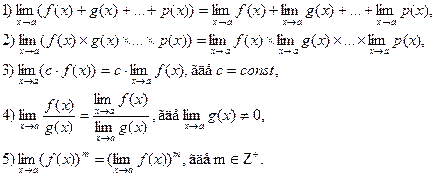
Функция f(x) называется непрерывнойв данной точке a, если выполняется равенство 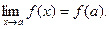
Замечательные пределы:
1. 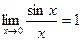 – первый замечательный предел.
– первый замечательный предел.
2. 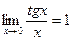 – второй замечательный предел.
– второй замечательный предел.
3. 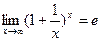 – третий замечательный предел.
– третий замечательный предел.
Техника вычисления пределов
Пример 1.
Найти 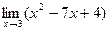 .
.
Решение.
Функция 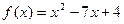 – непрерывная, графиком ее является парабола. Следовательно, заменяя ее аргумент предельным значением, найдем значение предела:
– непрерывная, графиком ее является парабола. Следовательно, заменяя ее аргумент предельным значением, найдем значение предела:
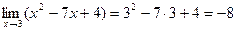 .
.
Ответ: –8.
Пример 2.
Найти 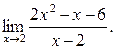
При непосредственном нахождении предела и числитель и знаменатель обращаются в нуль, таким образом, получается неопределенность вида 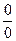 .
.
Чтобы раскрыть неопределенность 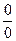 , разложим числитель на множители:
, разложим числитель на множители:
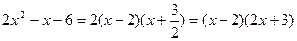 ,
,
и сократим дробь на выражение (х – 2), предел которого при 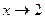 равен 0.
равен 0.
Тогда
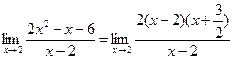 .
.
Ответ: 7.
Пример 3.
Найти 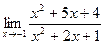 .
.
Решение:
Непосредственно подстановкой убеждаемся, что выражение обращается в неопределенность вида 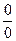 .
.
Разложим числитель и знаменатель на множители:
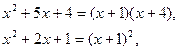
и сократим дробь на выражение (х + 1). Таким образом
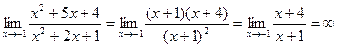 .
.
Ответ: ¥.
Пример 4.
Найти: 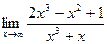 .
.
Решение:
При 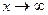 непосредственно подстановкой имеем неопределенность вида
непосредственно подстановкой имеем неопределенность вида 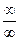 .
.
Чтобы раскрыть неопределенность, разделим числитель и знаменатель дроби на наивысшую степень переменной – 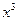 . Тогда
. Тогда
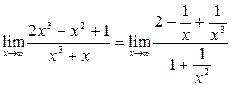 .
.
Поскольку 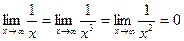 , то
, то 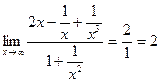 .
.
Ответ: 2.
Пример 5.
Найти: 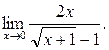
Решение.
Непосредственно подстановкой имеем неопределенность 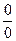 .
.
Раскроем неопределенность, умножив числитель и знаменатель на число, сопряженное к знаменателю дроби: 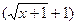
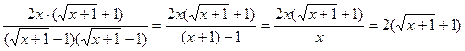 .
.
Тогда
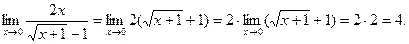
Ответ: 4.
Пример 6.
Найти: 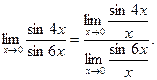
Решение:
Найдем пределы, используя первый замечательный предел 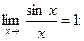
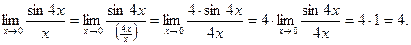
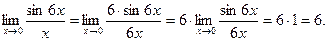
Таким образом: 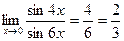 .
.
Замечание:
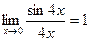 , так как если
, так как если 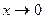 , то
, то 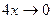 .
.
Значит 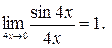
Ответ: 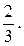
Пример 7.
Найти: 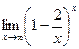 .
.
Решение:
Преобразуем выражение, стоящее под знаком предела, к виду 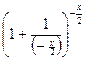 ,
,
и используем второй замечательный предел 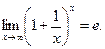
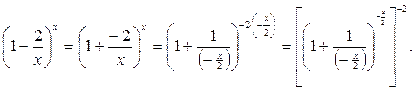
Если 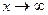 , то
, то 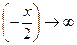 . Значит:
. Значит:

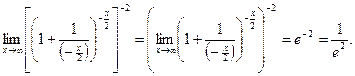
Ответ: 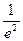 .
.
Дифференциальное исчисление
По данной теме сначала изучите главу 6 §6.1-6.9 учебника [ 1] или главу 1 §1.1-1.11 учебника [ 2]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия.
Производная функции
Производной функции f(x) в точке x0 называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует и конечен.
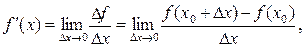
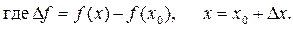
Справедливы следующие правила:
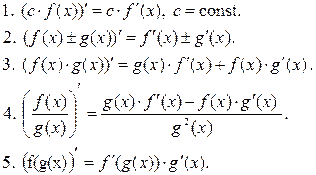
Нахождение производной называется дифференцированием функции.
Основные формулы дифференцирования:
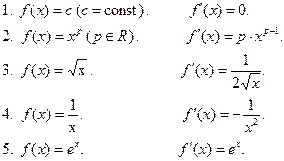
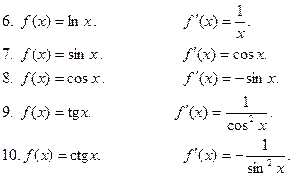
Пример 1. Найти значение производной функции f(x) в точке 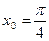 ,
,
если 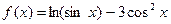 .
.
Решение.
Функция f(x) представляет собой алгебраическую сумму двух функций:
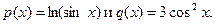
Следовательно: 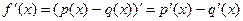 по правилу 2.
по правилу 2.
Функция p(x) есть композиция логарифмической и тригонометрической функций, а значит, по правилу 5 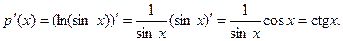
Функция q(x) есть композиция степенной и тригонометрической функций, следовательно, по правилам 1, 5
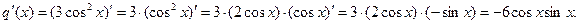
Таким образом:
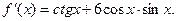
при 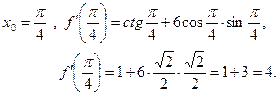
Ответ: 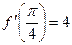 .
.
Пример 2. Найти значение производной функции f(x) в точке x0 = 2, если  .
.
Решение:
Функция f(x) представляет собой произведение двух функций: 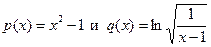 .
.
Следовательно, по правилу 3 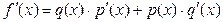 .
.
Согласно правилу 2, 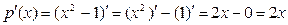 .
.
Функция q(x) есть композиция функций: логарифмической и линейной, так как
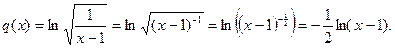
При преобразовании функции q(x) были использованы свойства степени и свойства логарифма.
Таким образом:
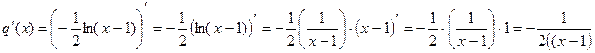
по правилам 1, 5.
Найдем 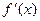 :
:
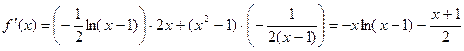 .
.
При x0 = 2
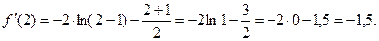
Ответ: