Производные высших порядков. Производная называется производной 1-го порядка

Производная называется производной 1-го порядка. Однако производная сама является функцией, которая также может иметь производную.

Производной n-го порядка называется производная от производной (n-1)-го порядка.

Обозначается: и т.д.

Механический смысл 2-й производной: 2-ая производная пути во времени равна ускорению точки в момент .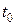

Основные теоремы дифференциального начисления

Теорема Ферма. Если дифференцируемая на промежутке X функция достигает наибольшего или наименьшего значения во внутренней точке 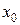этого промежутка, то производная функции в этой точке равна нулю, т.е. .

Теорема Ролля. Пусть функция непрерывна на , дифференцируема на и . Тогда внутри отрезка существует хотя бы одна точка , в которой производная равна нулю: .

Теорема Лагранжа. Пусть функция непрерывна на отрезке и дифференцируема на . Тогда внутри отрезка существует хотя бы одна точка , в которой:

или .

Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле. Другими словами, если имеется неопределенность вида или , то

Дифференциал

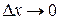Пусть функция определена на промежутке Xи дифференцируема в окрестности точки . Тогда существует конечная производная . Отсюда , где бесконечно малая при , или .

Таким образом, приращение функции 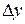состоит из двух слагаемых – линейного относительно 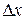и нелинейного, представляющего бесконечно малую более высокого порядка, чем .

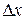Дифференциалом функции называется главная, линейная относительно 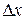часть приращения функции, равная произведению производной на приращение независимой переменной:

.

Например, дифференциал функции равен , откуда . Поэтому формулу для дифференциала функции можно записать в виде:

откуда .

Геометрический смысл дифференциала: дифференциал равен приращению ординаты касательной, проведенной к графику функции в данной точке, когда xполучает приращение 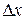(см. рис. выше).

Свойства дифференциала в основном аналогичны свойством производной:

1. .

2. .

3. .

4. .

5.

Рассмотрим сложную функцию . Если функции и 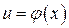– дифференцируемые функции своих аргументов, то производная сложной функции равна . Тогда дифференциал функции .Таким образом, . Это означает, что формула дифференциала не изменяется, если вместо функции от независимой переменной x рассмотреть функцию от зависимой переменной u. Это свойство дифференциала называется инвариантностью формы дифференциала.