Дополнительные задачи и упражнения 4 страница
b) 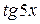 через
через 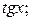
c) 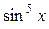 в виде многочлена первой степени от тригонометрических функций углов, кратных x.
в виде многочлена первой степени от тригонометрических функций углов, кратных x.
4. Найти сумму всех корней n-ой степени из 1.
5. Вычислить
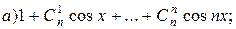
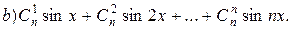
6. Доказать, что четыре точки 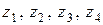 тогда и только тогда лежат на одной окружности, когда дробь
тогда и только тогда лежат на одной окружности, когда дробь 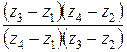 является действительным числом.
является действительным числом.
7. Доказать, что все (кроме 1) корни 7-й степени из 1, являются первообразными.
8. Вычислить: 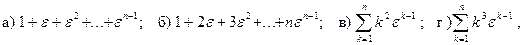 где
где 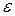 - первообразный корень n-й степени из единицы.
- первообразный корень n-й степени из единицы.
9. Выяснить геометрический смысл преобразований комплексной плоскости, определяемых функциями f(z), g(z) и h(z)=f(g(z):
a) 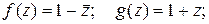
b) б) 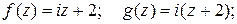
c) в) 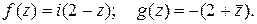
АЛГЕБРА МНОГОЧЛЕНОВ
Понятия:
1) многочлен от x; степень многочлена;
2) равенство многочленов;
3) сумма и произведение многочленов;
4) делимость;
5) НОД многочленов;
6) приводимые и неприводимые многочлены;
7) взаимно простые многочлены;
8) корень многочлена;
9) кратный корень.
Факты:
1) теорема о делении многочлена с остатком;
2) теорема о НОД в алгоритме Евклида;
3) представление НОД многочленов в виде их комбинации;
4) свойства делимости многочленов;
5) теорема о разложении на неприводимые множители;
6) теорема Безу;
7) делимость на x-c ;
8) признак кратности корня;
9) теорема о существовании корня многочлена над полем комплексных чисел (без доказательства);
10) разложение многочленов в произведение неприводимых множителей над полем комплексных чисел и над полем действительных чисел;
11) формулы Виета и Лагранжа.
Многочлен  степени n над полем P определяется как выражение вида
степени n над полем P определяется как выражение вида 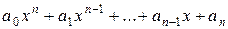 . Здесь
. Здесь 


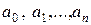
 - коэффициенты из некоторого числового поля P,
- коэффициенты из некоторого числового поля P, 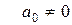 ,
, 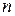 -
-  целое неотрицательное число,
целое неотрицательное число, 
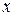
 - переменная, причем,
- переменная, причем, 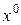 отожествляют с единицей.
отожествляют с единицей.
Число 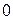 также является многочленом, но степень его не определена. Над многочленами выполняют действия сложения, вычитания, умножения по правилам, известным из средней школы. Относительно этих действий множество
также является многочленом, но степень его не определена. Над многочленами выполняют действия сложения, вычитания, умножения по правилам, известным из средней школы. Относительно этих действий множество 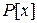 всех многочленов над полем
всех многочленов над полем 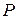 образует кольцо (но не поле, ибо операция деления в
образует кольцо (но не поле, ибо операция деления в 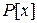 выполняется не всегда, даже если речь идет не о делении на
выполняется не всегда, даже если речь идет не о делении на 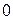 ). Однако, в кольце
). Однако, в кольце 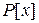 выполнимо деление с остатком: для произвольного многочлена
выполнимо деление с остатком: для произвольного многочлена 
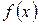 и ненулевого многочлена
и ненулевого многочлена 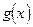 существует единственная пара многочленов
существует единственная пара многочленов 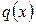 - частное и
- частное и 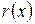 - остаток, таких, что
- остаток, таких, что 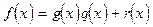
 и при
и при 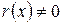 степень
степень 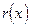 меньше степени
меньше степени 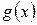 .
.
Если 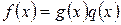 , то говорят, что
, то говорят, что 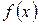 делится на
делится на 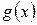 . Процедуру деления с остатком выполняют в обычной форме.
. Процедуру деления с остатком выполняют в обычной форме.
Пример 1. Разделить с остатком многочлен 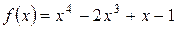 на многочлен
на многочлен 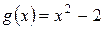 .
.
   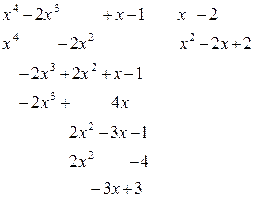 |
Получим 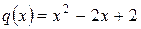 ,
, 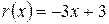 . g
. g
Деление с остатком используют при решении задачи о нахождении наибольшего общего делителя многочленов 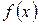 и
и 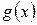 - НОД
- НОД 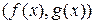 . Точнее, применяется алгоритм последовательного деления, известный под названием алгоритм Евклида:
. Точнее, применяется алгоритм последовательного деления, известный под названием алгоритм Евклида:
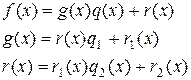
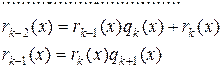
Здесь 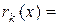 НОД
НОД 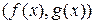 .
.
Пример 2. Найти наибольший общий делитель многочленов
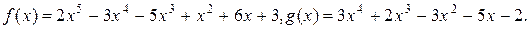
 1 Чтобы избежать дробных коэффициентов (а НОД находится с точностью до постоянного ненулевого множителя), умножим
1 Чтобы избежать дробных коэффициентов (а НОД находится с точностью до постоянного ненулевого множителя), умножим  на 3:
на 3:

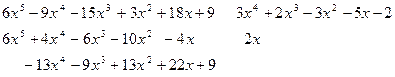
Умножим полученную разность на 3 и продолжим деление. При этом, конечно, частное исказится, но остаток определяется с точностью до множителя нулевой степени.

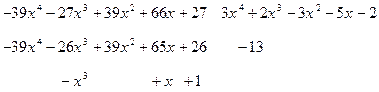
Предлагаем самим убедится, что 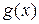 делится на
делится на 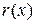 без остатка. Получили, что НОД
без остатка. Получили, что НОД 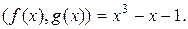 g
g
Алгоритм Евклида позволяет решать важную для приложений задачу о нахождении для многочленов  и
и 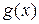 таких многочленов
таких многочленов 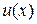 и
и 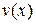 , что
, что
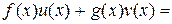 НОД
НОД 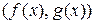 .
.
(Для взаимно простых многочленов последнее соотношение принимает вид 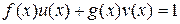 и является критерием взаимной простоты
и является критерием взаимной простоты 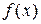 и
и 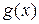 ). При этом из цепочки равенств, кроме последнего, полученных применением к многочленам
). При этом из цепочки равенств, кроме последнего, полученных применением к многочленам 
 и
и 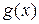 алгоритма Евклида, следует последовательно исключить
алгоритма Евклида, следует последовательно исключить 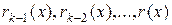 , выразив
, выразив 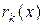 через
через  и
и 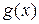 с “многочленными коэффициентами”
с “многочленными коэффициентами” 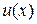 и
и 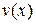 .
.
Понятно, что при решении этой задачи деление с остатком следует выполнять, не пренебрегая множителями нулевой степени.
Пример 3. Для многочленов 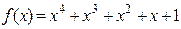 и
и 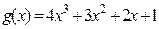 найти многочлены
найти многочлены 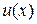 и
и 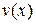 такие, что
такие, что 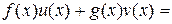 НОД
НОД 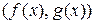 .
.
1 Предлагаем самостоятельно применить к данным многочленам алгоритм Евклида и убедиться в том, что 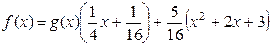 ,
,
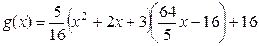 .
.
Здесь 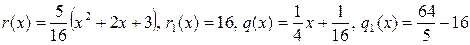 .
.
Понятно, что 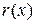 делится на число 16, поэтому НОД(
делится на число 16, поэтому НОД( 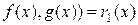 ). Итак, из соотношений
). Итак, из соотношений 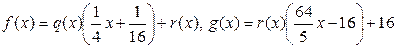 нам надо исключить
нам надо исключить 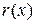 . В итоге получим
. В итоге получим 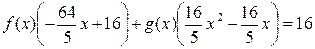 .
.
В случае необходимости, последнее равенство можно разделить на 16. g
Число 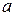 называется корнем многочлена
называется корнем многочлена  , если
, если 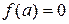 . Критерием того, что
. Критерием того, что 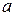 есть корень многочлена, является делимость
есть корень многочлена, является делимость  на
на 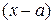 (без остатка!). Этот критерий легко доказать на основании теоремы Безу: остаток от деления многочлена
(без остатка!). Этот критерий легко доказать на основании теоремы Безу: остаток от деления многочлена  на
на 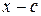 равен
равен 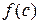 .
.
Сформулированный критерий позволяет дать определение кратного корня. Число 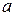 является корнем многочлена
является корнем многочлена  кратности
кратности 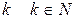 , если
, если  делится на
делится на 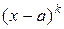 и
и  не делится на
не делится на 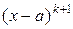 . Известно, что если
. Известно, что если 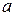 является корнем многочлена
является корнем многочлена  кратности
кратности 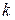 , то для производной
, то для производной 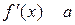 является корнем кратности
является корнем кратности 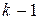 .
.
Деление многочлена  на бином
на бином 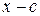 удобно проводить с помощью схемы Горнера, которая основана на рекуррентных соотношениях:
удобно проводить с помощью схемы Горнера, которая основана на рекуррентных соотношениях: 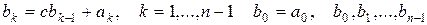 - коэффициенты частного, а
- коэффициенты частного, а 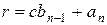 - остаток. Схема Горнера состоит из двух строк. В первой располагаются коэффициенты многочлена
- остаток. Схема Горнера состоит из двух строк. В первой располагаются коэффициенты многочлена  , а вторая заполняется последовательно коэффициентами частного
, а вторая заполняется последовательно коэффициентами частного 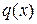 и остатком r (иногда впереди еще ставят значение c).
и остатком r (иногда впереди еще ставят значение c).
 Пример 4. Разделить по схеме Горнера многочлен
Пример 4. Разделить по схеме Горнера многочлен 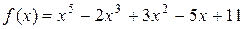 на
на 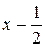 .
.
 1
1 
Таким образом, 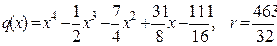 .
.
Из сказанного выше вытекает, что число 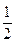 не является корнем многочлена
не является корнем многочлена  . Более того,
. Более того, 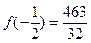 . g
. g
Схема Горнера позволяет многочлен  , записанный по убыванию степени x, разложить по степеням бинома
, записанный по убыванию степени x, разложить по степеням бинома 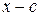 , а также определить кратность корня.
, а также определить кратность корня.
Пример 5. Найти корни многочлена 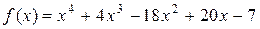
 кратности выше первой и определить эту кратность.
кратности выше первой и определить эту кратность.
1 Поскольку корни кратности больше 1 являются и корнями производной, то найдем: 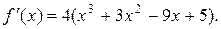 Нетрудно заметить, что число 1 является корнем многочлена
Нетрудно заметить, что число 1 является корнем многочлена 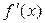 . Проверим является ли 1 корнем многочлена
. Проверим является ли 1 корнем многочлена  и если да, то какой кратности. Для этого делим на
и если да, то какой кратности. Для этого делим на 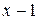 многочлен
многочлен  , потом частное и т.д.
, потом частное и т.д.
| -18 | -7 | ||||
| -13 | |||||
| -7 | |||||
| 8 ¹ 0 |
Итак, 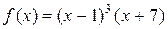 , т.е. число 1 есть корень многочлена
, т.е. число 1 есть корень многочлена  кратности 3. g
кратности 3. g
Находить рациональные корни многочлена с целочисленными коэффициентами поможет следующий факт: если несократимая дробь 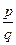 является корнем такого многочлена, то
является корнем такого многочлена, то 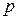 является делителем свободного члена, а
является делителем свободного члена, а 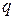 - делителем старшего коэффициента.
- делителем старшего коэффициента.
Пример 6. Разложить многочлен 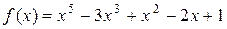 по степеням двучлена
по степеням двучлена 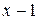 .
.
1 Речь идет о представлении данного многочлена в виде
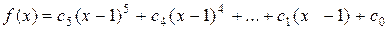 .
.
Известно, что 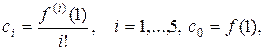 но коэффициенты
но коэффициенты 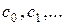 удобно находить, вычисляя последовательно остатки от деления
удобно находить, вычисляя последовательно остатки от деления  на
на 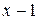 , полученного частного на
, полученного частного на 
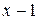 , нового частного на
, нового частного на 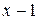 и т.д.
и т.д.
| -3 | -2 | |||||
| -2 | -1 | -3 | -2 | |||
| -1 | -4 | |||||
Таким образом,
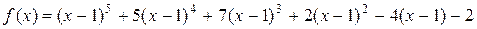 .
.
Заметим, что
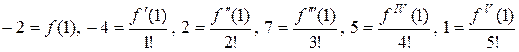 , откуда легко найти значение
, откуда легко найти значение 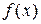 и всех его производных при
и всех его производных при 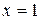 . g
. g
В первом индивидуальном задании нужно было построить многочлен степени, не превышающей 4, по его значениям в пяти точках. Интерполяционная формула Лагранжа позволяет сразу вычислить многочлен  степени
степени 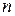 , если известно, что
, если известно, что 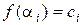 при
при 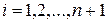 . А именно:
. А именно:
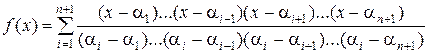 .
.
Пример 7. Построить многочлен  четвертой степени такой, что
четвертой степени такой, что 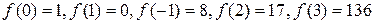 .
.
1 Согласно формуле Лагранжа, 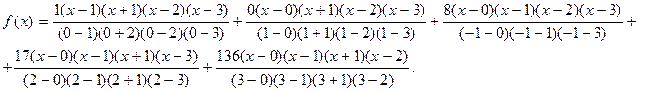 После упрощения будем иметь:
После упрощения будем иметь: 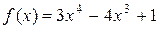 . g
. g
Если  ,
, 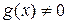 - некоторые многочлены над полем
- некоторые многочлены над полем 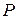 , то рациональная дробь над этим полем определяется как отношение
, то рациональная дробь над этим полем определяется как отношение 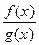 . Рациональная дробь называется правильной, если степень числителя
. Рациональная дробь называется правильной, если степень числителя  меньше степени знаменателя, а среди правильных дробей выделяют простейшие или элементарные. Элементарные дроби имеют вид
меньше степени знаменателя, а среди правильных дробей выделяют простейшие или элементарные. Элементарные дроби имеют вид 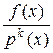 , где
, где 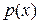 - неприводимый над полем P многочлен (т.е. многочлен, который нельзя представить в виде произведения двух многочленов над полем P степени меньшей, чем степень многочлена
- неприводимый над полем P многочлен (т.е. многочлен, который нельзя представить в виде произведения двух многочленов над полем P степени меньшей, чем степень многочлена 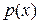 ),
), 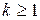 и степень
и степень  меньше степени
меньше степени 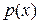 .
.
Известно, что всякая правильная рациональная дробь однозначно разлагается в сумму простейших.
Пример 8. Разложить в сумму простейших над полем действительных чисел рациональную дробь 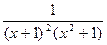 .
.
1 Знаменатель данной дроби разложен в произведение неприводимых многочленов над полем R 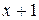 и
и 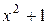 . Решим задачу методом неопределенных коэффициентов, основываясь на том, что знаменателями простейших дробей могут быть многочлены
. Решим задачу методом неопределенных коэффициентов, основываясь на том, что знаменателями простейших дробей могут быть многочлены 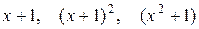 :
: 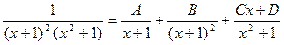 .
.
Здесь 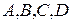 - неизвестные коэффициенты числителей элементарных дробей. Приведя правую часть последнего равенства к общему знаменателю и приравняв числители обеих частей, будем иметь:
- неизвестные коэффициенты числителей элементарных дробей. Приведя правую часть последнего равенства к общему знаменателю и приравняв числители обеих частей, будем иметь: 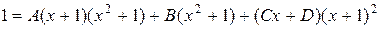 . Значение неизвестных коэффициентов можно найти из системы линейных уравнений, которую получим, дав неизвестному x четыре значения. Например, положив последовательно
. Значение неизвестных коэффициентов можно найти из системы линейных уравнений, которую получим, дав неизвестному x четыре значения. Например, положив последовательно 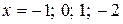



 будем иметь
будем иметь
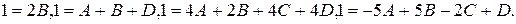 Откуда
Откуда 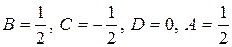 , т.е.
, т.е. 
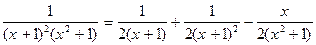 . g
. g
Контрольные вопросы
1. Существует ли многочлен третьей степени с действительными коэффициентами, все корни которого мнимые?
2. Существует ли многочлен 4-й степени с действительными коэффициентами, имеющий трехкратный корень i+2 ?
3. Существует ли многочлен 4-й степени с действительными коэффициентами, имеющий корни i+1, i+2, i+3 ?
4. Существует ли многочлен 4-й степени с действительными коэффициентами, имеющий корни 2+i, 2-i, 3+i?
5. Может ли многочлен x3+px+q с нечетными целыми коэффициентами p и q иметь целый корень?
6. Известно, что число c является k-кратным корнем многочлена  и s-кратным корнем многочлена
и s-кратным корнем многочлена 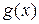 . Какую кратность имеет корень c для многочлена
. Какую кратность имеет корень c для многочлена 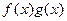 ? Ответ обосновать.
? Ответ обосновать.
7. Известно, что число c является k-кратным корнем многочлена 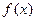 и s-кратным корнем многочлена
и s-кратным корнем многочлена 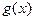 . Какую кратность имеет корень c для многочлена
. Какую кратность имеет корень c для многочлена 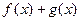 ? Ответ обосновать.
? Ответ обосновать.
8. Составить многочлен наименьшей степени с целыми коэффициентами, имеющий корень i-3.
9. Существует ли многочлен третьей степени с рациональными коэффициентами, имеющий только один иррациональный корень?
