Разрешимые группы и их простые свойства
Определение 2.1.1. Конечная группа  называется разрешимой, если
называется разрешимой, если  обладает нормальным рядом с абелевыми факторами.
обладает нормальным рядом с абелевыми факторами.
Поскольку при уплотнении нормального ряда с абелевыми факторами нормальными подгруппами получается нормальный ряд с абелевыми факторами, то определение конечной разрешимой группы можно сформулировать следующим образом.
Определение 2.1.2. Конечная группа  называется разрешимой, если
называется разрешимой, если  обладает главным рядом с абелевыми факторами.
обладает главным рядом с абелевыми факторами.
Поскольку любой главный ряд группы можно уплотнить до композиционного ряда, а факторы композиционного ряда являются простыми группами (в частности, простая абелева группа — это в точности группа простого порядка), то определение конечной разрешимой группы можно сформулировать следующим образом.
Определение 2.1.3. Конечная группа  называется разрешимой, если
называется разрешимой, если  обладает композиционным рядом с факторами простого порядка.
обладает композиционным рядом с факторами простого порядка.
Рассмотрим еще один подход к определению разрешимой группы, справедливый и для бесконечных групп. Для этого рассмотрим определение ряда коммутантов группы, а также свойства -го коммутанта группы.
Определение 2.1.4. Ряд коммутантов группы  определяется следующим образом:
определяется следующим образом: 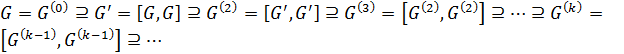 (1).
(1).
Замечание 2.1.1. Поскольку коммутант группы является ее нормальной подгруппой, то ряд (1) является нормальным.
Лемма 2.1.1 (Свойства k-го коммутанта группы). Пусть  — группа,
— группа, 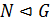 . Тогда:
. Тогда:
1) 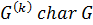 для любого
для любого 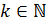 .
.
2) 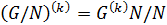 для любого
для любого 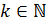 .
.
3) Пусть 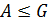 .
. 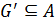 тогда и только тогда, когда
тогда и только тогда, когда 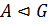 и
и 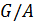 — абелева.
— абелева.
Определение 2.1.5. 1) Группа  называется разрешимой, если
называется разрешимой, если 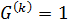 для некоторого
для некоторого 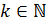 , то есть если ряд коммутантов группы
, то есть если ряд коммутантов группы  обрывается на единичной подгруппе.
обрывается на единичной подгруппе.
2) 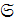 — множество всех разрешимых групп.
— множество всех разрешимых групп.
Теорема 2.1.1 (Свойства разрешимых групп).
1) Всякая подгруппа разрешимой группы является разрешимой.
2) Всякая факторгруппа разрешимой группы является разрешимой.
3) Если 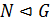 ,
, 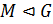 ,
, 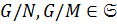 , то
, то 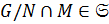 .
.
4) Если 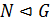 ,
, 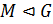 ,
, 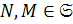 , то
, то 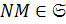 .
.
5) Если 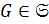 ,
, 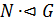 , то
, то 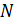 — элементарная абелева -группа для некоторого
— элементарная абелева -группа для некоторого 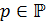 .
.
6) Если 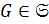 ,
, 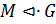 , то
, то 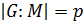 для некоторого
для некоторого 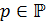 .
.
7) Если 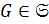 ,
, 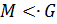 , то
, то 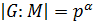 для некоторого
для некоторого 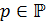 ,
, 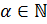 .
.
Доказательство. 1) Пусть 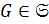 ,
, 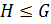 . Тогда
. Тогда 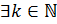 , такой, что
, такой, что 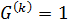 . Так как
. Так как 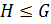 , то по лемме 1.2.1
, то по лемме 1.2.1 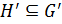 , и значит,
, и значит, 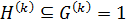 . Следовательно,
. Следовательно, 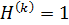 для некоторого
для некоторого 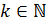 , поэтому
, поэтому 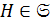 .
.
2) Пусть 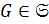 ,
, 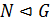 . Тогда
. Тогда 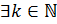 , такой, что
, такой, что 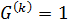 . Учитывая лемму 1.1(2),
. Учитывая лемму 1.1(2), 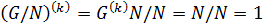 . Следовательно,
. Следовательно, 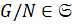 .
.
3) Пусть 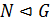 ,
, 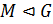 ,
, 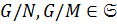 . Тогда
. Тогда 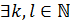 , такие, что
, такие, что 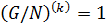 и
и 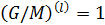 . По лемме 1.2.1 получаем, что
. По лемме 1.2.1 получаем, что 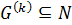 и
и 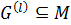 . Так как
. Так как 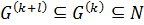 и
и 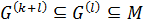 , то
, то 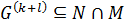 и, согласно лемме 1.2.2,
и, согласно лемме 1.2.2, 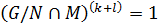 . Следовательно,
. Следовательно, 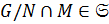 .
.
4) Пусть 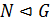 ,
, 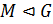 ,
, 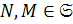 . По теореме 1.2.1(1)
. По теореме 1.2.1(1) 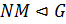 . Так как
. Так как 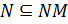 , то по теореме 1.2.1(3)
, то по теореме 1.2.1(3) 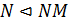 , и значит, можно рассматривать
, и значит, можно рассматривать 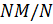 . По теореме 2.1.1(3)
. По теореме 2.1.1(3) 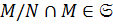 . Так как
. Так как 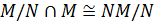 , то
, то 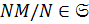 . Тогда по лемме 1.2.3
. Тогда по лемме 1.2.3 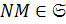 .
.
5) Пусть 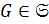 ,
, 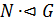 . Так как
. Так как 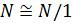 — главный фактор группы
— главный фактор группы  , то по определению 2.1.1
, то по определению 2.1.1 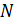 — абелева. Поскольку
— абелева. Поскольку 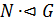 , то по теореме 1.2.2
, то по теореме 1.2.2
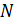 — характеристически простая группа, и по теореме 1.2.3
— характеристически простая группа, и по теореме 1.2.3 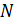 — прямое произведение изоморфных простых групп. Так как
— прямое произведение изоморфных простых групп. Так как 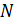 — абелева, то
— абелева, то 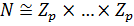 для некоторого
для некоторого 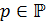 , и значит,
, и значит, 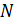 — элементарная абелева -группа по определению 1.1.1.
— элементарная абелева -группа по определению 1.1.1.
6) Пусть 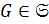 ,
, 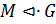 . Тогда
. Тогда 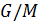 — простая абелева группа. Следовательно,
— простая абелева группа. Следовательно, 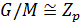 , и значит,
, и значит, 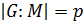 .
.
Теорема доказана.
Лемма 2.1.2. Нильпотентные группы разрешимы.
Доказательство. Пусть  — нильпотентная группа и
— нильпотентная группа и 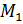 <·
<·  . По Следствию 1.2.4., подгруппа
. По Следствию 1.2.4., подгруппа 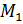 нормальна и |
нормальна и |  :
: 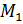 | — простое число. По теореме 1.2.4.
| — простое число. По теореме 1.2.4.
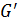 ≤
≤ 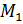 . Если теперь
. Если теперь 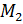 < ·
< · 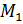 , то опять
, то опять
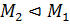 , |
, | 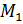 :
: 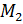 | — простое число и
| — простое число и
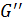 ≤
≤ 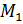 0 ≤
0 ≤ 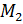 . Пусть
. Пусть
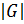 =
=  — каноническое разложение числа
— каноническое разложение числа 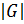 и
и 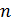 =
= 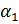 +
+ 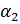 + ... +
+ ... + 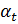 .
.
Тогда 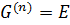 и
и  — разрешимая группа ступени не выше
— разрешимая группа ступени не выше 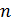 . Лемма доказана.
. Лемма доказана.
Теорема 2.1.2. 1. Главные факторы разрешимой неединичной группы
являются элементарными абелевыми примарными группами.
2. Композиционные факторы разрешимой неединичной группы имеют простые порядки.
Доказательство. 1. Пусть 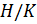 — главный фактор группы
— главный фактор группы  . Тогда
. Тогда 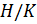 — минимальная нормальная подгруппа факторгруппы
— минимальная нормальная подгруппа факторгруппы 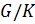 . Поэтому
. Поэтому 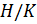 — элементарная абелева примарная группа по (1).
— элементарная абелева примарная группа по (1).
2. Пусть 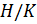 — композиционный фактор группы
— композиционный фактор группы  . Тогда K — наибольшая нормальная подгруппа в
. Тогда K — наибольшая нормальная подгруппа в 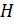 и
и 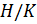 — простая группа по теореме 1.2.5. Так как
— простая группа по теореме 1.2.5. Так как 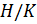 разрешима, то
разрешима, то 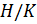 отлична от своего коммутанта, поэтому
отлична от своего коммутанта, поэтому 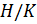 абелева и по теореме 1.2.6, имеет простой порядок.
абелева и по теореме 1.2.6, имеет простой порядок.
