Екі нүкте арқылы өтетін түзудің теңдеуі.

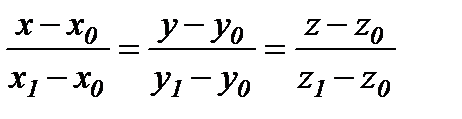
Түзудің канондық теңдеуі

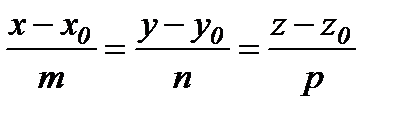
Түзудің параметрлік теңдеуі.

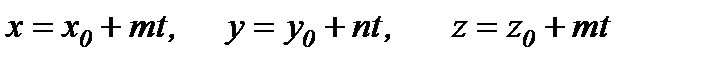
Түзудің жалпы теңдеуі.

,

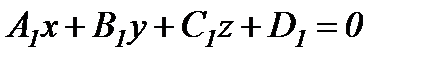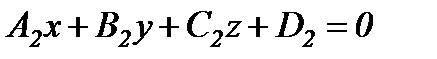
№20

Фокустар деп аталатын берілген екі нүктеден қашықтықтарының қосындысы тұрақты шама болатын жазықтықтағы нүктелердің геометриялық орындарын эллипс деп атайды.

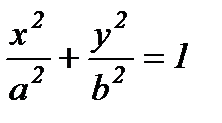
Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырмасының абсолюттік шамасы тұрақты 2а-ға тең болатын жазықтықтағы нүктелердің геометриялық орындарын гиперболадеп атайды.

Гиперболаның канондық теңдеуі былай жазылады:

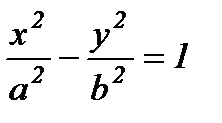
Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден ара қашықтықтары бірдей болатын жазықтықтағы нүктелердің геометриялық орындарын парабола дейді.

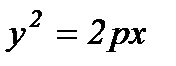
№21

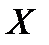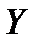. жәнебос емес сандар жиындары болсын. Егер 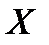жиынының кез келген 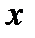элементіне белгілі бір заңдылықпен 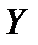жиынының бір 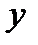элементі сәйкес келетін болса, онда 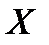жиынында 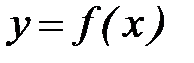функциясы берілді дейді. Мұндай жағдайда 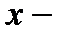ті тәуелсіз шама (аргумент), ал 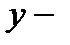ті тәуелді шама деп атайды.

Функцияның үш түрлі жолмен беріледі:

а)Аналитикалық тәсілмен;

б) Таблицалық, яғни мәндер тәсілімен;

в) Графиктік тәсілмен

№22

Функцияның нүктедегі шегі

Егер кез келген 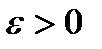саны үшін 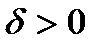саны табылып, кезкелге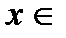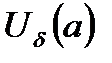н үшін 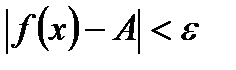теңсіздігі орындалса, онда 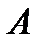саны 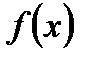функциясының 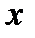шамасы 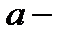ға ұмтылғандағы 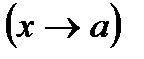шегі деп аталады да, 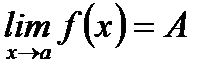түрінде белгіленеді.

Функцияның ақырсыздықтағы шегі

Анықтама. Кезкелген 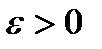( 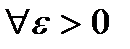) саны үшін қандай да бір 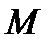саны табылып, 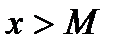болғанда 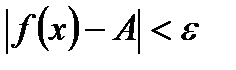орындалса, онда 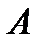саны 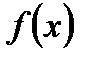функциясының 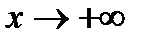шегі деп аталады және 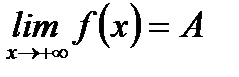түрінде белгіленеді.

Шексіз аз және шексіз үлкен функциялар.

Анықтама. Егер 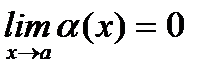болса, онда теңдігі орындалса, онда 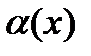функциясы 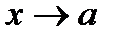( 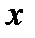шамасы 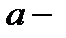ға ұмтылғанда)шексіз аз шама (ш.а.ш.) деп аталады.

Анықтама. Егер 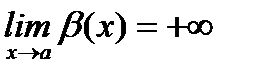болса, онда 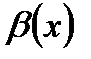функциясы 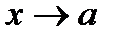-ғы шексіз үлкен шама (ш.ү.ш.) деп атайды.

№23

Шектер туралы негізгі теоремалар.Егер 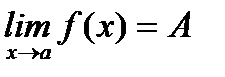, , 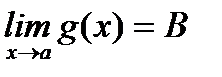болса, онда

1.

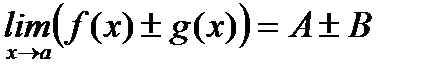
2.

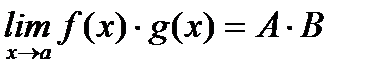
3.Кезкелге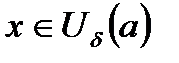н үшін, 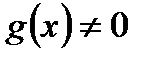және 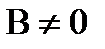болса, онда .

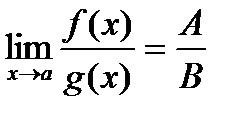№24

Бірінші тамаша шек.Құрамында тригонометриялық функциялар бар өрнектердің шектерін есептегенде бірінші тамаша шекті қолданады: 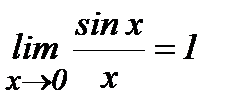.Дәлелдеу: Радиусы бірге тең шеңбер аламыз. ,

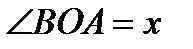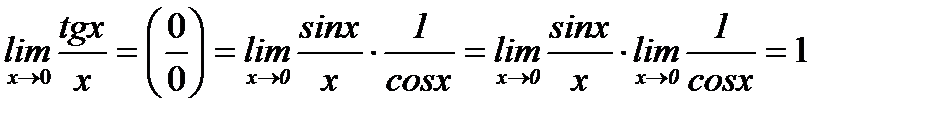
Екінші тамаша шек: .

Мұндағы е»2,718282… – иррационал сан.

№25

Егер 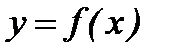функциясы келтірілген үш шартты қанағаттандырса, онда оны 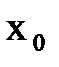нүктесінде үзіліссіз дейді

Егер 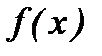функциясың 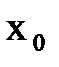нүктесінде оң жақты және сол жақты шектері бар болып, бірақ олар өзара тең болмаса, онда 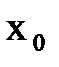нүктесі 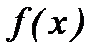функциясының біріншітекті үзіліс нүктесі деп аталады. Егер оң жақты және сол жақты шектердің ең болмағанда біреуі не шексіздікке тең болып, не жоқ болса, онда 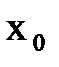нүктесі 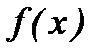функциясының екіншітекті үзіліс нүктесі деп аталады. Егер 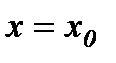нүктесінде ақырлы оң жақты және сол жақты шектер бар болып, бірақ олар осы нүктедегі функцияның мәніне тең болмаса, онда 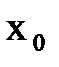нүктесі 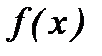функциясының түзетілетін үзіліс нүктесі деп аталады.

№26

Егер 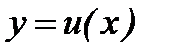және 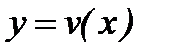дифференцианалданатын болса, онда бұл функциялардың қосындысы, көбейтіндісі және қатынасы да (қатынастың бөлімі 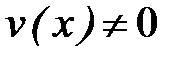) осы нүктеде дифференцианалданады және мына формулалар орынды:

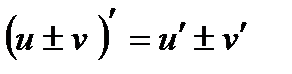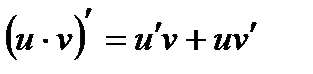1. 2. 3. .

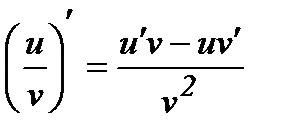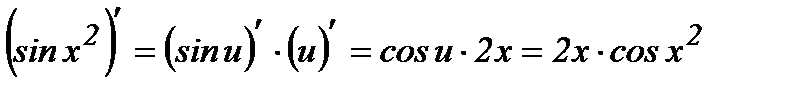
Дифференциалды есептеу

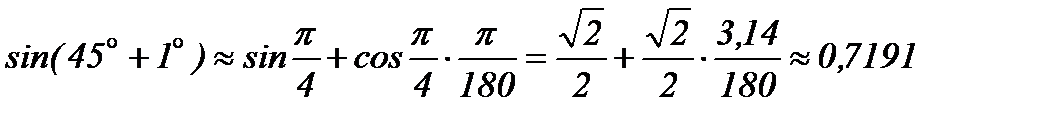
№27

Лопиталь жок ,,,

№28

Теорема (экстремумның қажетті шарты).Егер дифференциалданатын 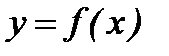функциясының 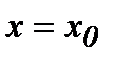нүктесінде экстремумы бар болса, онда сол нүктеде 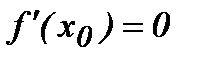болады. Осы теоремадан мынадай қорытындыға келеміз: егер 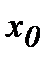нүктесінде функцияның экстремумы бар болса, онда ол нүктеде оның туындысы нөлге тең, не ол нүктеде туындысы болмауы мүмкін. Кері тұжырым әрқашан орындала бермейді.

Теорема (экстремумнің жеткілікті шарты). Егер 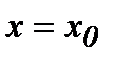нүктесінде 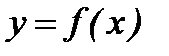функциясының туындысы нөлге тең болса және 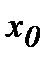нүктесінен өткенде 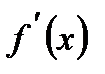таңбасын өзгертсе, онда 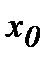нүктесі экстремум нүктесі болады: 1) егер таңба «плюс»-тен «минус»-ке өзгерсе, онда 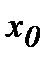– максимум нүктесі; 2) егер таңба «минус»-тен «плюс»-ке өзгерсе, онда 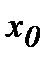– минимум нүктесі болады.