Тәжірибелік сабақ. Жазықтықтағы түзу
Тапсырмалар.1. АЖ: [7] № 2.142, 2.144, 2.146, 2.150, 2.152, 2.164, 2.172, 2.
2. ҮЖ: [7] № 2.141, 2.143, 2.151, 2.153, 2.155, 2.165, 2.175.
Әдістемелік ұсыныстар.
1. Түзудің жазықтықта әртүрлі орналасулары оның жалпы теңдеуіндегі коэффициенттеріне байланысты болады:
а) Егер 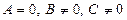 болса, онда
болса, онда 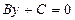 түзуі
түзуі 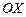 өсіне параллель болады.
өсіне параллель болады.
ә) Егер 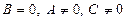 болса, онда
болса, онда 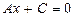 түзуі
түзуі 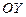 өсіне параллель болады.
өсіне параллель болады.
б) Егер 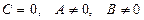 болса, онда
болса, онда 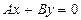 түзуі координат жүйесінің бас нүктесінен өтеді.
түзуі координат жүйесінің бас нүктесінен өтеді.
в) Егер 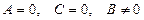 болса, онда
болса, онда 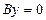 түзуі
түзуі 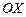 өсімен беттесетін болады.
өсімен беттесетін болады.
г) Егер 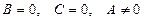 болса, онда
болса, онда 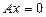 түзуі
түзуі 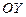 өсімен беттесетін болады.
өсімен беттесетін болады.
2. Түзудің әртүрлі теңдеулерінің бір түрінен екіншісіне көшуге болады. Сондықтан есептің шартынан параметрлері тез анықталатын теңдеудің түрін таңдауға болады.
1-есеп. Берілген 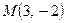 нүктеден өтіп ордината өсін 5-ке тең кесіндіде қиятын түзудің теңдеуін табыңыз.
нүктеден өтіп ордината өсін 5-ке тең кесіндіде қиятын түзудің теңдеуін табыңыз.
Шешімі. Іздестіріп отырған түзудің теңдеуін бұрыштық коэффициент теңдеуі түрінде анықтайық, 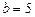 . Енді
. Енді 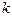 - бұрыштық коэффициентін табайық. Іздестіріп отырған түзу берілген
- бұрыштық коэффициентін табайық. Іздестіріп отырған түзу берілген 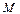 нүктеден өтетін болғандықтан, оның координаттары осы түзудің теңдеуін қанағаттандырады, яғни
нүктеден өтетін болғандықтан, оның координаттары осы түзудің теңдеуін қанағаттандырады, яғни 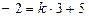 . Осыдан
. Осыдан 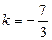 . Сонымен,
. Сонымен, 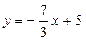 .
.
2-есеп. Төмендегі түзулердің жазықтықтағы орналасуын анықтау керек:
а) 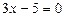 б)
б) 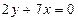 в)
в) 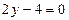 г)
г) 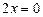 д)
д) 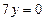
Шешуі: а) 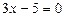 теңдеуінде
теңдеуінде 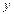 айнымалы шама жоқ. Сондықтан, ол
айнымалы шама жоқ. Сондықтан, ол 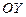 өсіне параллель түзу және
өсіне параллель түзу және 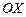 өсін
өсін 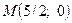 нүктеде қияды:
нүктеде қияды:
б) 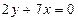 теңдеуінде бос мүше жоқ. Сондықтан, берілген түзу координат жүйесінің бас нүктесінен өтеді;
теңдеуінде бос мүше жоқ. Сондықтан, берілген түзу координат жүйесінің бас нүктесінен өтеді;
в) 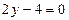 теңдеуінде
теңдеуінде 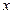 - айнымалы шамасы жоқ. Сондықтан, ол
- айнымалы шамасы жоқ. Сондықтан, ол 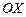 өсіне параллель түзу және
өсіне параллель түзу және 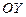 өсін
өсін 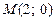 нүктеде қияды;
нүктеде қияды;
г) 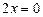 теңдеуінде
теңдеуінде 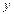 - айнымалы шама жоқ. Сондықтан, ол
- айнымалы шама жоқ. Сондықтан, ол 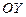 өсімен беттеседі.
өсімен беттеседі.
3-есеп. 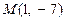 нүктеден өтіп
нүктеден өтіп 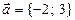 векторына перпендикуляр болатын түзудің жалпы және бұрыштық теңдеуін анықтау керек.
векторына перпендикуляр болатын түзудің жалпы және бұрыштық теңдеуін анықтау керек.
Шешуі. 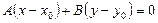 теңдеуіндегі
теңдеуіндегі 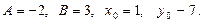 Сонда
Сонда 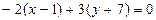 болады. Сонымен,
болады. Сонымен, 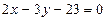 түзудің жалпы теңдеуі, ал
түзудің жалпы теңдеуі, ал 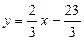 түзудің бұрыштық теңдеуі болады, мұндағы
түзудің бұрыштық теңдеуі болады, мұндағы 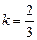 - бұрыштық коэффициент.
- бұрыштық коэффициент.
Негізгі әдебиет: [7], 2 тарау, § 2 (п.1) (71-76 беттер).
Қосымша әдебиет: [19], 1 тарау, § 1-7 (5-24 беттер), 3 тарау, § 12-16 (35-57 беттер).
Бақылау сұрақтары:
1. Түзудің 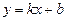 теңдеуіндегі
теңдеуіндегі 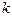 коэффициентінің мағынасы қандай?
коэффициентінің мағынасы қандай?
2. Жазықтықтағы түзудің нормаль векторының координаттарын қалай анықтайды?
3. Түзудің кез келген теңдеуіндегі параметрлерін оның жалпы теңдеуіндегі коэффициенттер арқылы өрнектеуе бола ма?
№5-тәжірибелік сабақ. Кеңістіктегі түзу мен жазықтық
Тапсырмалар.1. АЖ: [7] № 2.182, 2.184, 2.190, 2.186, 2.196, 2.198, 2.204, 2.208.
2. ҮЖ: [7] № 2.183, 2.185, 2.197, 2.199, 2.201, 2,205, 2.210.
Әдістемелік ұсыныстар.
1. Жазықтықтың кеңістікте әртүрлі орналасуы оның 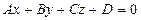 жалпы теңдеуіндегі коэффициенттеріне байланысты болады:
жалпы теңдеуіндегі коэффициенттеріне байланысты болады:
а) Егер 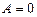 болса, онда жазықтық
болса, онда жазықтық 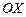 өсіне параллель болады. Егер
өсіне параллель болады. Егер 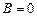 болса, онда жазықтық
болса, онда жазықтық 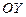 өсіне параллель болады. Егер
өсіне параллель болады. Егер 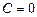 болса, онда жазықтық
болса, онда жазықтық 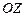 өсіне параллель болады.
өсіне параллель болады.
ә) Егер 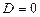 болса, онда жазықтық декарт координат жүйесінің бас нүктесінен өтеді.
болса, онда жазықтық декарт координат жүйесінің бас нүктесінен өтеді.
б) Егер 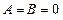 болса, онда жазықтық
болса, онда жазықтық 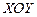 координат жазықтығына параллель болады. Егер
координат жазықтығына параллель болады. Егер 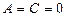 болса, онда жазықтық
болса, онда жазықтық 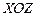 координат жазықтығына параллель. Егер
координат жазықтығына параллель. Егер 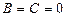 болса, онда жазықтық
болса, онда жазықтық 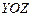 координат жазықтығына параллель болады.
координат жазықтығына параллель болады.
в) Егер 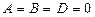 болса, онда жазықтық
болса, онда жазықтық 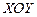 координат жазықтығын анықтайды. Егер
координат жазықтығын анықтайды. Егер 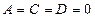 болса, онда жазықтық
болса, онда жазықтық 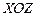 координат жазықтығын анықтайды. Егер
координат жазықтығын анықтайды. Егер 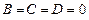 болса, онда жазықтық
болса, онда жазықтық 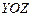 координат жазықтығын анықтайды.
координат жазықтығын анықтайды.
г) Егер 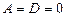 болса, онда жазықтық
болса, онда жазықтық 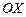 өсі арқылы өтеді. Егер
өсі арқылы өтеді. Егер 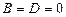 болса, жазықтық
болса, жазықтық 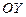 өсі арқылы өтеді. Егер
өсі арқылы өтеді. Егер 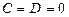 болса, жазықтық
болса, жазықтық 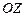 өсі арқылы өтеді.
өсі арқылы өтеді.
2. Жазықтық өзінің үш нүктесі арқылы немсе бір нүктесі және бағыты (өзіне перпендикуляр вектор-нормаль векторы) арқылы толық анықталады.
3. Түзу өзінің екі нүктесі арқылы немесе бір нүктесі және бағыты (өзіне параллель вектор-бағыттаушы векторы) арқылы толық анықталады.
4. Екі немесе екі жазықтық арасындағы бұрыш олардың бағыт векторлары арасындағы бұрышқа тең; бағыт векторлары арқылы түзулер мен жазықтықтардың параллельдігін, перпендикулярлығын анықтауға болады.
1-есеп. Берілген 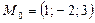 нүктеден өтіп, нормаль векторы
нүктеден өтіп, нормаль векторы 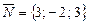 болатын жазықтықтың теңдеуін анықтаңыз.
болатын жазықтықтың теңдеуін анықтаңыз.
Шешуі. Іздестіріп отырған жазықтықтың теңдеуін табу үшін 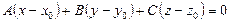 формуланы пайдаланамыз, мұндағы
формуланы пайдаланамыз, мұндағы 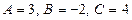 ,
, 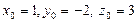 , сонда
, сонда 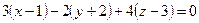 . Осыдан іздестіріп отырған жазықтықтың теңдеуін табамыз:
. Осыдан іздестіріп отырған жазықтықтың теңдеуін табамыз: 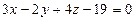 .
.
2-есеп. 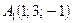 нүктеден және
нүктеден және 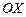 өсінен өтетін жазықтықтың теңдеуін анықтаңыз.
өсінен өтетін жазықтықтың теңдеуін анықтаңыз.
Шешуі. 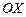 өсінен өтетін жазықтықтың теңдеуі мына түрде анықталады:
өсінен өтетін жазықтықтың теңдеуі мына түрде анықталады: 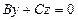 . Мұндағы
. Мұндағы 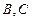 - белгісіз коэффициенттер және ол берілген
- белгісіз коэффициенттер және ол берілген 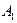 нүктеден өтетін болғандықтан, оның координаттары осы теңдеуді қанағаттандырады, яғни
нүктеден өтетін болғандықтан, оның координаттары осы теңдеуді қанағаттандырады, яғни 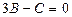 немесе
немесе 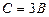 . С-ның мәнін бастапқы теңдеуге қойып, іздестіріп отырған жазықтықтың теңдеуін анықтаймыз:
. С-ның мәнін бастапқы теңдеуге қойып, іздестіріп отырған жазықтықтың теңдеуін анықтаймыз: 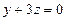 .
.
3-есеп. Берілген 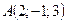 нүктеден өтіп
нүктеден өтіп 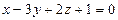 жазықтығына перпендикуляр болатын түзудің теңдеуін анықтаңыз.
жазықтығына перпендикуляр болатын түзудің теңдеуін анықтаңыз.
Шешуі. Берілген жазықтықтың 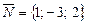 -нормаль векторы іздестіріп отырған түзудің бағыттауыш векторы болып табылады. Олай болса, берілген нүктеден өтіп бағыттауыш векторы
-нормаль векторы іздестіріп отырған түзудің бағыттауыш векторы болып табылады. Олай болса, берілген нүктеден өтіп бағыттауыш векторы 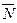 болатын түзу теңдеуі
болатын түзу теңдеуі 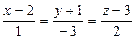 болады.
болады.
Негізгі әдебиет: [7], 2 тарау, § 2 (п.2) (77-84 беттер).
Қосымша әдебиет: [19], 9 тарау, § 38-43 (141-165 беттер).
Бақылау сұрақтары:
1. Жазықтықтың нормаль векторының координаттарын қалай анықтайды?
2. Екі түзу немесе екі жазықтық, түзу мен жазықтық арасындағы бұрыштар қандай векторлармен анықталады?
3. Кеңістіктегі түзудің жалпы теңдеуі қалай анықталады?
