Решение задачи

Для надежной эксплуатации элемента необходимо, чтобы число запасных элементов n отвечало условию 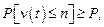где Р = 0.90; 0.95 и 0.99. Следовательно:

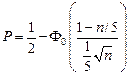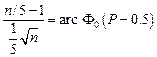и . n » 9

8 Поясните понятие «коэффициент готовности». Как определяется коэффициент готовности в стационарном режиме эксплуатации элемента в случае Пуассоновского потока отказов и восстановлений?

Коэффициентом готовности k_г(t) называют вероятность того, что в момент времени t

элемент находится в исправном состоянии.

Допустим, что случайные времена эксплуатации и восстановления распределены по

экспоненциальному закону. При этом потоки отказов и восстановлений являются

потоками Пуассона.

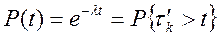- закон распределения времени эксплуатации

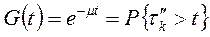- закон распределения времени восстановления

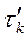‑ случайное время эксплуатации k-го элемента

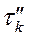‑ случайное время ремонта k-го элемента

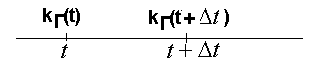Пусть величина k_г(t) определена. Необходимо определить величину k_г(t+Δt).

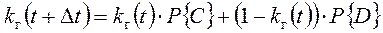
Элемент останется в работе за время Δt, если за это время не будет отказов (событие С),

или произойдёт восстановление (событие D).

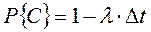‑ вероятность отсутствия отказа за время Δt

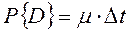‑ вероятность, что за время Δt будет восстановление

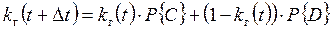‑ определение коэффициента готовности

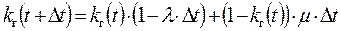
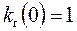‑ вначале элемент всегда в рабочем состоянии

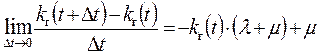‑ переход к производной k_г(t)

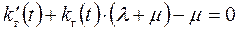‑ для решения дифференциального уравнения удобно применить операторный метод.

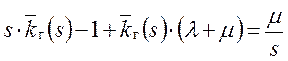
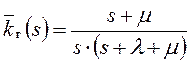
Переходя к оригиналу, получим:

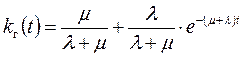
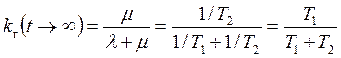
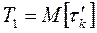‑ мат. ожидание времени эксплуатации

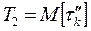‑ мат. ожидание времени восстановления

№9 Поясните понятие « последовательное и параллельное соединение элементов в смысле надежности». При известной функции надежности единичного элемента запишите выражения для функции надежности системы, состоящей либо из последовательного, либо из параллельного соединения элементов в смысле надежности.

При последовательном соединении элементов в смысле надежности понимается такое их соединение, при котором отказ любого элемента приводит к отказу системы в целом.

При параллельномсоединении элементов в смысле надежности понимается такое их соединение, при котором отказ системы происходит лишь при отказе всех элементов.

Безотказная работа системы состоящей из последовательно соединенных элементов это одновременное наступление событий безотказной работы всех элементов.

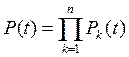Для независимых событий вероятность есть произведение их вероятностей. Значит, функция надежности системы есть произведение функций надежности:

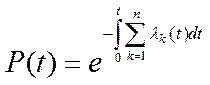Функция надежности через интенсивности отказов элементов:

Отказ системы состоящей из параллельно соединенных элементов это одновременное наступление событий отказов всех элементов.

Функция ненадежности системы есть произведение функций ненадежности:

;

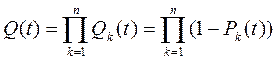Функция надежности системы:

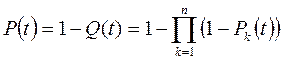10 Как определяются средние времена эксплуатации системы, состоящей либо из последовательного, либо из параллельного соединения элементов в смысле надежности, если интенсивности отказов всех элементов одинаковы?

Последовательное соединение

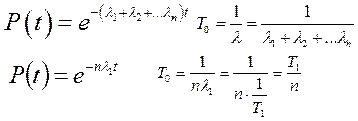Параллельное соединение

		- постоянная Эйлера

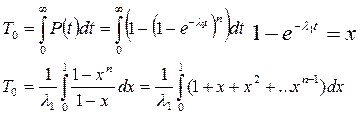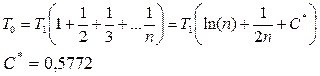- постоянная Эйлера

11. Нарисуйте граф процесса гибели и размножения. Как Вы примените этот граф к решению задачи об определении вероятности состояний технической системы с резервированием?

Процесс гибели и размножения является одним из способов описания системы с восстанавливаемыми элементами. Основным предположением является то, что законы распределения отказов и восстановлений элемента – экспоненциальные.

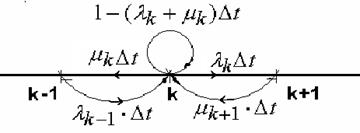
Если в момент времени t процесс находится в состоянии k, то за время Δt могут иметь

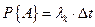место следующие несовместные события:

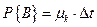A – процесс перейдёт в состояние k+1;

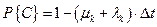B – процесс перейдёт в состояние k-1;

C – процесс останется в состоянии k.

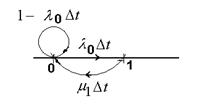
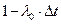
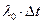Из состояния 0 система может перейти в состояние 1 с вероятностью:

либо остаться в состоянии 0 с вероятностью:

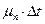
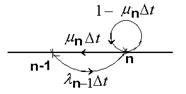Из состояния n система может перейти в состояние n-1 с вероятностью:

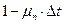либо остаться в состоянии n с вероятностью:

Найдём вероятность того, что за малое время Δt система останется в состоянии k:

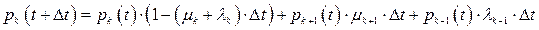
Переходя к производной получим систему дифференциальных уравнений:

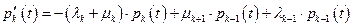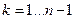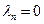
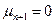
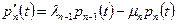
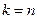
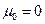
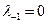
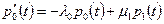
Крайние положения системы:

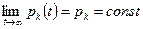На практике обычно рассматривается стационарный процесс гибели и размножения, при t→∞. При этом имеет место следующее свойство:

Переходя к пределу при t→∞ получим систему алгебраических уравнений:

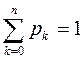
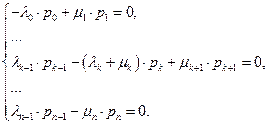Вероятность, что система находится в одном из состояний равна 1

В результате решения получим:

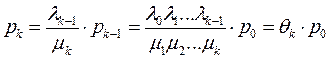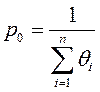Одной из основных характеристик процесса является среднее состояние:

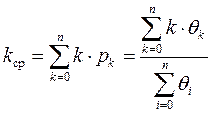
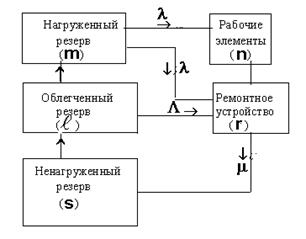Пусть в данной системе под состоянием k

подразумевается число неисправных элементов.

λ_k – суммарная интенсивность отказов

μ_k – суммарная интенсивность восстановлений

Суммарное число элементов: N=n+m+l+s.

Система работает исправно, пока число рабочих

элементов не меньше n.

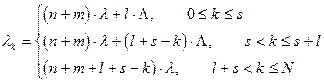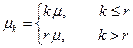13) Что Вы понимаете под предупредительными заменами стареющих элементов, основанными на наработке на отказ? Каким образом определяются плановые сроки замены оборудования при его предупредительных заменах?

Предупредительной заменой называется такая замена, при которой элемент заменяется либо через плановый срок службы t_пл, либо после его выхода из строя, если это время наступает раньше t_пл.

Функция надёжности элемента при предупредительных заменах

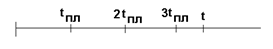Характеристика надёжности – среднее время наработки на отказ при предупредительных заменах

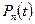
- функция надёжности при n предупредительных заменах

- функция надёжности элемента без учёта предупредительных замен

Рассмотрим функцию надёжности при одной предупредительной замене:

Событие A заключается в том, что элемент проработает в течение времени t

Событие B – элемент проработал в течение времени t_пл.

Событие C – заменённый элемент проработал в течение времени t-t_пл.

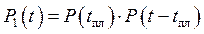
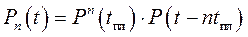При n предупредительных заменах:

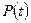Определение среднеговремениэксплуатации с учётом предупредительных замен

Следует отметить, что при экспоненциальном законе надёжности (без старения),

выигрыша от предупредительных замен нет:

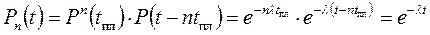
Средний срок службы элемента при n предупредительных заменах:

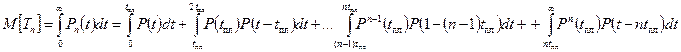
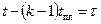
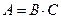Выполняется замена переменной:

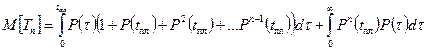
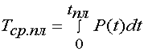
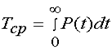
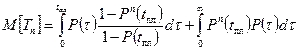
Определение среднего времени эксплуатации с учётом предупредительных замен

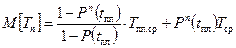- среднее время эксплуатации элемента при n плановых заменах

При бесконечном количестве плановых замен среднее время эксплуатации

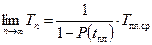стремится к пределу:

14. Как определяется среднее время эксплуатации стареющего элемента, эксплуатируемого с предупредительными заменами?

Предупредительной заменой называется такая замена, при которой элемент заменяется либо через плановый срок службы t_пл, либо после его выхода из строя, если это время наступает раньше t_пл.

Функция надежности при n предупредительных заменах:

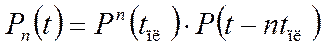Следует отметить, что при экспоненциальном законе надёжности (без старения), выигрыша от предупредительных замен нет:

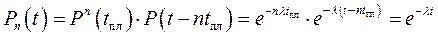Вывод:Средний срок службы элемента при n предупредительных заменах:

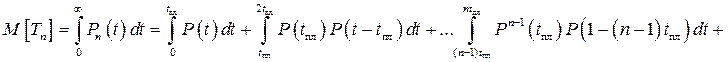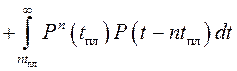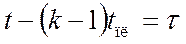Выполняется замена переменной:

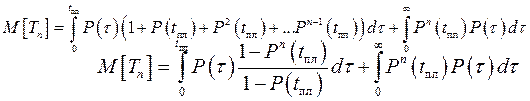Среднее время эксплуатации:

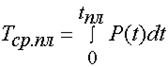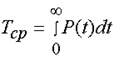Среднее время эксплуатации элемента при n плановых заменах: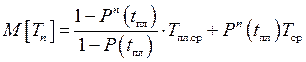

При бесконечном количестве плановых замен среднее время эксплуатации 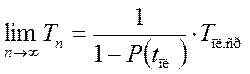стремится к пределу: