Гіпербола

Означення. Гіперболою називається множина точок площини, різниця відстаней яких від двох заданих точок, фокусів, є величина стала і дорівнює .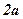

По аналогії з еліпсом фокуси розміщуємо в точках ,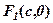

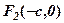(див. рис. 25-4).

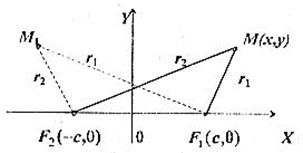
Рис. 25-4.

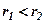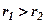Оскільки, як видно з рисунка, можуть бути випадки і , то згідно означення .

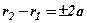Відомо, що в трикутнику різниця двох сторін менша третьої сторони, тому , наприклад, з 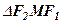маємо

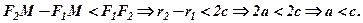
Отже, для гіперболи .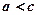

Далі запишемо значення виразів 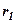і 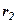через координати точок

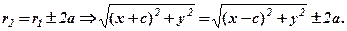
Піднесемо до квадрата обидві частини і після подальших перетворень знайдемо

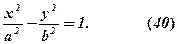
Пропонуємо завершити самостійно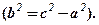

Гіпербола симетрична відносно координатних осей, тому, як і для еліпса, досить побудувати її графік в першій чверті, де 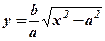. Область визначення для першої чверті .

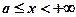При 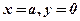маємо одну із вершин гіперболи 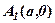. Друга вершина 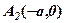. Якщо 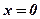, то із (40) 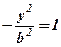, – дійсних коренів немає. Говорять, що 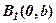і 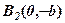– уявні вершини гіперболи. Із співвідношення 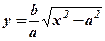випливає, що при досить великих значеннях 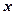має місце наближена рівність 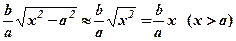. Тому пряма 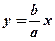є лінією, відстань між якою і відповідною точкою гіперболи прямує до нуля при .

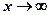Пряма 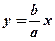називається асимптотою гіперболи. Згідно з симетрією існує ще одна асимптота .

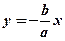Для побудови гіперболи необхідно відкласти на координатних осях відрізки довжиною 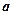на 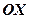по обидва боки від точки 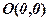і аналогічно відкласти 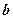по .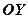

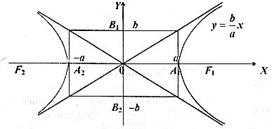
Рис. 26.

Після цього побудувати прямокутник зі сторонами паралельними координатним осям (див. рис. 26). Діагоналі прямокутника є асимптотами гіперболи. Через вершину 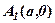в першій чверті проводимо вітку гіперболи, яка асимптотично наближається до прямої

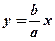. Інші вітки будуємо симетрично відносно 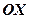і .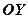

Ексцентриситет гіперболи 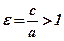, бо 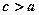. Якщо величину 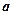зафіксувати, а 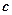збільшувати, то при цьому збільшується 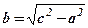, тому гіперболи будуть відхилятись від 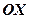, гіпербола буде розпрямлятись. При зменшені 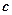буде зменшуватись 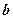, вітки гіперболи будуть наближатись до 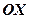. У випадку, коли 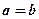, асимптотами будуть бісектриси координатних кутів,

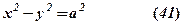
– рівнобічнагіпербола.