Составление дифференциального уравнения движения системы
Задание на расчет
1. Составить дифференциальное уравнение движения данной механической системы.
2. Найти закон движения системы, если в начальный момент времени центр масс ползуна смещен вниз по наклонной плоскости на величину 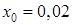 м от положения, в котором он находится при равновесии системы, после чего ему сообщена скорость
м от положения, в котором он находится при равновесии системы, после чего ему сообщена скорость 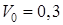 м/с, направленная вниз.
м/с, направленная вниз.
3. Провести анализ полученных результатов.
Для расчета принять: 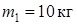 ,
, 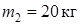 ,
, 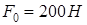 ,
, 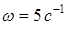 ,
,  ,
, 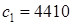 H/м,
H/м, 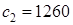 H/м.
H/м.
Составление дифференциального уравнения движения системы
Рассматриваемая система имеет одну степень свободы. Это обеспечивается принятыми условиями расчета, в частности, жесткостью стержня, соединяющего массы системы, и отсутствием проскальзывания при качении катка. Направим координатную ось x параллельно наклонной плоскости, совместив ее начало 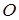 с положением центра масс ползуна при равновесии системы. В качестве координаты, определяющей положение системы, примем величину x — координату центра масс ползуна.
с положением центра масс ползуна при равновесии системы. В качестве координаты, определяющей положение системы, примем величину x — координату центра масс ползуна.
Для составления дифференциального уравнения движения системы применим теорему об изменении кинетической энергии в дифференциальной форме
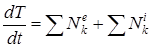 , (1.1)
, (1.1)
где 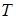 — кинетическая энергия системы,
— кинетическая энергия системы,
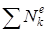 — сумма мощностей внешних сил, действующих на систему,
— сумма мощностей внешних сил, действующих на систему,
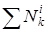 — сумма мощностей внутренних сил.
— сумма мощностей внутренних сил.
Так как тела системы являются абсолютно твердыми, а шарниры на концах стержня идеальными (без трения), то сумма мощностей внутренних сил системы равна нулю. Поэтому соотношение (1.1) запишется в виде
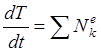 . (1.2)
. (1.2)
Построим расчетную схему задачи (рис.1.7). Изобразим на рисунке совокупность тел 1-2, свободную от внешних связей, в положении x > 0. Покажем на расчетной схеме скорости центров масс ползуна и катка, полагая их направленными в сторону возрастания координаты x, а также направление вращения катка. Заметим, что точка P катка является его мгновенным центром скоростей. Изобразим на расчетной схеме также внешние силы, действующие на систему:
1) силы тяжести ползуна 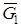 и катка
и катка 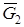 ;
;
2) возмущающую силу  ;
;
|
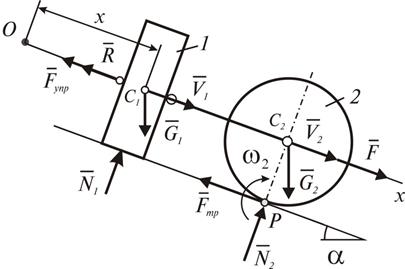
Рис. 1.7
3) реакции связей:
· реакцию направляющей ползуна 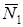 , эта сила перпендикулярна направляющей: ползун скользит без трения;
, эта сила перпендикулярна направляющей: ползун скользит без трения;
· реакции плоскости 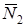 и
и 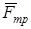 , приложенные к катку;
, приложенные к катку;
· равнодействующую реакций пружин 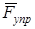 , направленную, в силу симметрии, по оси
, направленную, в силу симметрии, по оси 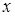 ;
;
· реакцию демпфера (силу сопротивления) 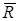 .
.
Вычислим кинетическую энергию системы как сумму кинетических энергий тел, входящих в ее состав:
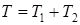 . (1.3)
. (1.3)
Кинетическая энергия ползуна, движущегося поступательно со скоростью V1 ,
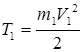 . (1.4)
. (1.4)
Кинетическая энергия катка, совершающего плоское движение,
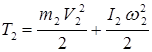 , (1.5)
, (1.5)
где
V2 — скорость центра масс катка,
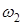 — угловая скорость катка,
— угловая скорость катка,
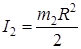 — момент инерции катка относительно оси, проходящей через его центр масс (R — радиус катка).
— момент инерции катка относительно оси, проходящей через его центр масс (R — радиус катка).
Подставляя формулы (1.4) и (1.5) в (1.3), получаем
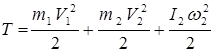 .
.
Так как  , а
, а 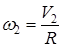 , то кинетическую энергию системы, с учетом выражения для момента инерции катка, можно записать в виде
, то кинетическую энергию системы, с учетом выражения для момента инерции катка, можно записать в виде
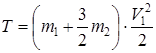
или, поскольку 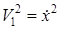 ,
,
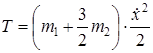 .
.
Назовем приведенной массой величину
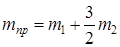 , (1.6)
, (1.6)
тогда кинетическая энергия системы
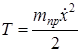 . (1.7)
. (1.7)
Вычислим производную по времени от кинетической энергии системы. Учитывая, что 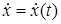 , а приведенная масса — величина постоянная, получаем
, а приведенная масса — величина постоянная, получаем
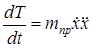 . (1.8)
. (1.8)
Вычислим сумму мощностей внешних сил. Известно, что мощность силы есть скалярное произведение силы на скорость точки ее приложения: 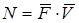 . Записывая скалярное произведение через проекции векторов, имеем:
. Записывая скалярное произведение через проекции векторов, имеем:
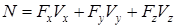 . (1.9)
. (1.9)
Эта формула удобна для вычисления мощности внешних сил, действующих на систему, так как скорости точек приложения большинства из них параллельны оси 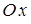 , поэтому в правой части (1.9) остается только первое слагаемое.
, поэтому в правой части (1.9) остается только первое слагаемое.
Используя формулу (1.9), получаем:
1) мощность силы тяжести ползуна: 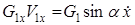 ,
,
2) мощность силы тяжести катка: 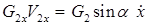 ,
,
3) мощность возмущающей силы: 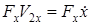 ,
,
4) мощность реакции пружин: 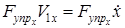 ,
,
5) мощность силы сопротивления: 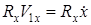 .
.
Кроме того, мощность силы 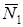 равна нулю, так как эта сила и скорость ее точки приложения взаимно перпендикулярны. Равны нулю также мощности сил
равна нулю, так как эта сила и скорость ее точки приложения взаимно перпендикулярны. Равны нулю также мощности сил 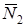 и
и 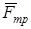 , так как равна нулю скорость их точки приложения.
, так как равна нулю скорость их точки приложения.
Таким образом,
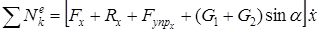 . (1.10)
. (1.10)
Заметим, что
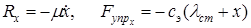 , (1.11)
, (1.11)
где
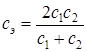 — коэффициент жесткости эквивалентной пружины,
— коэффициент жесткости эквивалентной пружины,
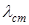 — статическая деформация эквивалентной пружины.
— статическая деформация эквивалентной пружины.
Замечание. Предлагаем убедиться самостоятельно в следующем: 1) две параллельно соединенные пружины жесткости с1 и с2 эквивалентны одной пружине, имеющей коэффициент жесткости 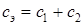 ; 2) две последовательно соединенные пружины жесткости с1 и с2 эквивалентны одной пружине, коэффициент жесткости которой находится из формулы ; 2) две последовательно соединенные пружины жесткости с1 и с2 эквивалентны одной пружине, коэффициент жесткости которой находится из формулы 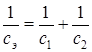 . . |
Подставляя (1.11) в (1.10), получаем
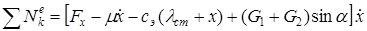
или
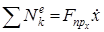 , (1.12)
, (1.12)
где
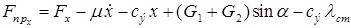 . (1.13)
. (1.13)
Приравнивая правые части (1.8) и (1.13) согласно (1.2), получаем после сокращения на 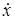 :
:
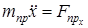 . (1.14)
. (1.14)
Найдем с помощью последнего соотношения и выражения для приведенной силы (1.13) условие равновесия системы. При равновесии системы 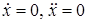 . Кроме того, равновесие невозможно при наличии возмущающей силы, т.е. в этом случае следует положить
. Кроме того, равновесие невозможно при наличии возмущающей силы, т.е. в этом случае следует положить 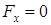 . Считая указанные условия выполненными, находим
. Считая указанные условия выполненными, находим
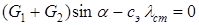 .
.
Следовательно, теперь приведенную силу можно записать в виде (здесь учтено выражение для проекции 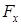 возмущающей силы):
возмущающей силы):
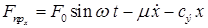 .
.
Подставив это выражение в уравнение (1.14), находим
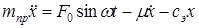 ,
,
откуда
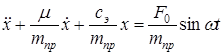 .
.
Введем обозначения
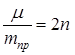 ,
, 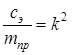 ,
, 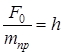 .
.
Тогда дифференциальное уравнение движения системы примет вид
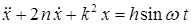 . (1.15)
. (1.15)
Таким образом, движение данной механической системы описывается неоднородным линейным дифференциальным уравнением второго порядка с постоянными коэффициентами. В уравнении (1.15): 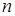 — коэффициент затухания;
— коэффициент затухания; 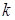 — круговая частота свободных колебаний;
— круговая частота свободных колебаний; 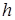 — относительная амплитуда возмущающей силы.
— относительная амплитуда возмущающей силы.
1.3.1.1. Рекомендации по составлению дифференциального уравнения движения с помощью теоремы о движении центра масс и теоремы об изменении кинетического момента (варианты 1–24)
1. Установить число степеней свободы системы выбрать систему отсчета и обобщенную координату — параметр 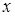 (все так же, как и в случае применения теоремы об изменении кинетической энергии).
(все так же, как и в случае применения теоремы об изменении кинетической энергии).
2. Применить теорему о движении центра масс к рассматриваемой системе, освобожденной от внешних связей (рис. 1.7). В проекциях на ось 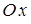 получим
получим
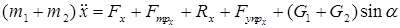 .
.
Здесь учтено, что 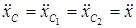 , а масса системы
, а масса системы 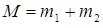 .
.
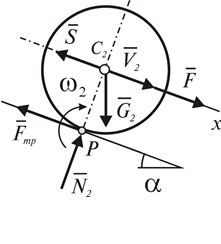 3. Применить теорему об изменении кинетического момента относительно оси
3. Применить теорему об изменении кинетического момента относительно оси 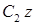 , проходящей через центр масс катка (рис. 1.8):
, проходящей через центр масс катка (рис. 1.8):
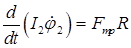 .
.
Здесь 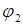 — угол поворота катка, отсчитываемый по ходу часовой стрелки (в соответствии с направлением отсчета координаты
— угол поворота катка, отсчитываемый по ходу часовой стрелки (в соответствии с направлением отсчета координаты 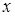 ).
).
4. Исключить силу трения из уравнений п.2 и п.3. Полученное уравнение привести к виду (1.15) с учетом кинематического соотношения 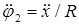 (т.
(т. 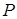 — мгновенный центр скоростей катка), выражения для проекций возмущающей силы
— мгновенный центр скоростей катка), выражения для проекций возмущающей силы 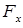 , силы сопротивления
, силы сопротивления 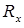 и упругой силы
и упругой силы 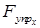 (см. условие примера и формулы (1.11)).
(см. условие примера и формулы (1.11)).
1.3.1.2. Рекомендации по составлению дифференциального уравнения движения системы с помощью теоремы об изменении кинетического момента (варианты 25–30)
Рассмотрим систему, изображенную на рис. 1.9. Система, совершает колебания за счет энергии, полученной в начальный момент: груз 1 смещен из положения равновесия на величину 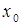 и ему сообщена скорость
и ему сообщена скорость 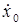 . Сопротивление не учитывается, нить нерастяжима и невесома, проскальзывание нити на блоке 2 отсутствует, каток 3 катится без скольжения.
. Сопротивление не учитывается, нить нерастяжима и невесома, проскальзывание нити на блоке 2 отсутствует, каток 3 катится без скольжения.
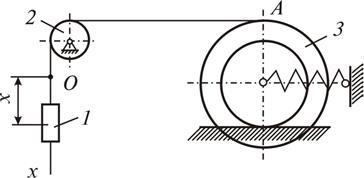
Рис. 1.9
Составление дифференциального уравнения движения системы рекомендуется проводить в следующем порядке:
1. Убедиться в том, что система имеет одну степень свободы, выбрать систему отсчета и обобщенную координату — параметр 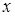 . Ось
. Ось 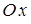 направлена вертикально вниз, а ее начало
направлена вертикально вниз, а ее начало 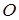 совпадает с положением центра масс груза 1 при равновесии системы. Выбрать направления отсчета углов поворота блока
совпадает с положением центра масс груза 1 при равновесии системы. Выбрать направления отсчета углов поворота блока 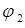 и катка
и катка 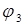 , согласовав их с направлением отсчета координаты
, согласовав их с направлением отсчета координаты 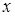 , т.е. положительным направлением отсчета обоих углов является направление, противоположное ходу часовой стрелки.
, т.е. положительным направлением отсчета обоих углов является направление, противоположное ходу часовой стрелки.
2. Расчленить систему на две части по горизонтальной ветви нити: 1) левую часть — совокупность тел 1 и 2; 2) правую часть — каток 3.
| а) | 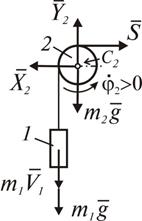 | б) | 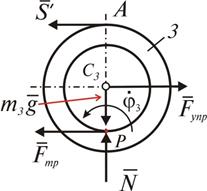 |
Рис. 1.10
Построить расчетные схемы для каждой из частей, изобразив на них заданные силы и реакции внешних связей: силы тяжести 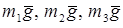 , реакции подшипников блока
, реакции подшипников блока 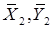 , реакцию нити на блок —
, реакцию нити на блок — 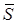 , реакцию нити на каток
, реакцию нити на каток 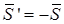 (нить невесома), реакцию пружины
(нить невесома), реакцию пружины 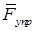 и реакции плоскости — нормальную
и реакции плоскости — нормальную 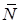 и силу трения
и силу трения 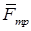 (рис. 1.10).
(рис. 1.10).
| |
3. К левой части (рис. 1.10, а) применить теорему об изменении кинетического момента относительно оси вращения блока 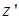 :
:
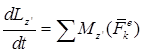 .
.
где  — кинетический момент груза и блока относительно оси
— кинетический момент груза и блока относительно оси 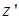 , а правая часть равенства — сумма моментов внешних сил относительно той же оси.
, а правая часть равенства — сумма моментов внешних сил относительно той же оси.
Для этого:
а) записать кинетический момент системы относительно оси 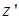 как функцию проекции скорости груза
как функцию проекции скорости груза 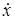 ; поскольку кинетический момент груза —
; поскольку кинетический момент груза — 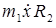 , а кинетический момент блока —
, а кинетический момент блока — 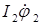 , то
, то
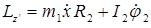 .
.
Так как нить на блоке не проскальзывает, то угловая скорость блока 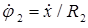 , поэтому
, поэтому
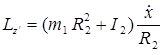 .
.
б) найти производную
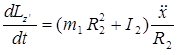 .
.
в) записать сумму моментов внешних сил
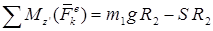 .
.
г) приравнять правые части последних соотношений согласно теореме моментов:
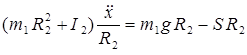 . (A)
. (A)
Это — дифференциальное уравнение движения левой части системы. Оно содержит неизвестную силу 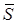 — реакцию нити.
— реакцию нити.
4. К правой части системы (рис. 1.10, б) применить теорему об изменении кинетического момента относительно неподвижного центра 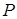 , принадлежащего плоскости и находящегося в данный момент в контакте с катком. Упомянутую теорему используем относительно оси
, принадлежащего плоскости и находящегося в данный момент в контакте с катком. Упомянутую теорему используем относительно оси 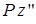 , перпендикулярной плоскости катка
, перпендикулярной плоскости катка
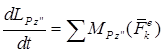 .
.
Дальнейшие действия аналогичны действиям, описанным в п. 3.
Необходимо:
а) найти кинетический момент катка относительно оси 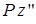 как функцию
как функцию 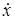
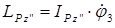 .
.
где 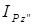 — момент инерции катка относительно оси
— момент инерции катка относительно оси 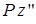 , а
, а 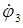 — проекция угловой скорости катка на ту же ось.
— проекция угловой скорости катка на ту же ось.
Модули скоростей груза и точек нити, включая точку 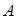 (рис. 1.10), равны, так как нить является нерастяжимой. Такую же величину имеет скорость верхней точки катка. Поэтому угловая скорость катка
(рис. 1.10), равны, так как нить является нерастяжимой. Такую же величину имеет скорость верхней точки катка. Поэтому угловая скорость катка 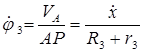 и
и
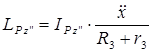 .
.
Для вычисления момента инерции 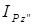 можно использовать теорему Гюйгенса-Штейнера:
можно использовать теорему Гюйгенса-Штейнера: 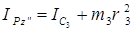 , где
, где 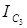 — момент инерции катка относительно оси, проходящей через его центр масс параллельно оси
— момент инерции катка относительно оси, проходящей через его центр масс параллельно оси 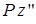 .
.
б) найти производную
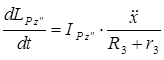 .
.
.
в) найти сумму моментов внешних сил, приложенных к катку, относительно оси 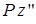 :
:
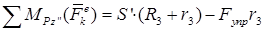 .
.
г) приравнять, согласно теореме моментов, правые части последних соотношений:
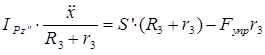 . (Б)
. (Б)
Это — дифференциальное уравнение движения катка. Оно содержит неизвестную силу 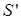 — реакцию нити.
— реакцию нити.
5. Получить дифференциальное уравнение движения данной системы, исключив из уравнений (А) и (Б) неизвестную силу 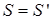 . Привести полученное уравнение к виду
. Привести полученное уравнение к виду
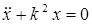 , (В)
, (В)
где 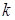 — круговая частота свободных колебаний системы (здесь выражение для
— круговая частота свободных колебаний системы (здесь выражение для 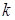 не приводится). При этом следует учесть, что в силу выбора системы отсчета
не приводится). При этом следует учесть, что в силу выбора системы отсчета 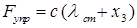 , где
, где 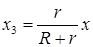 — смещение центра масс катка от положения, которое он занимает при равновесии системы.
— смещение центра масс катка от положения, которое он занимает при равновесии системы.
