Диаграммы режимов работы СМО M/M/1. Установившийся режим

С нагрузкой тесно связан другой показатель качества – коэффициент использования, или коэффициент загрузки обслуживающего устройства. Этот показатель качества, обозначаемый через 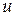, определяется как доля времени, в течение которого обслуживающее устройство занято. Рассмотрим достаточно длительный интервал времени T.В СМО с l обслуживающими устройствами на каждое из них в среднем за время T придется по 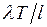заявок в предположении, что поток заявок равномерно распределяется по l устройствам. Поскольку каждая заявка требует в среднем длительности обслуживания 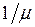, то общее среднее время занятости обслуживающего устройства составит 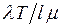(сюда включены и простои обслуживающего устройства). Поделив эту величину на T, получим 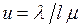. Поскольку обслуживающее устройство не может быть занято более 100 % времени, то коэффициент использования не может превосходить единицу. Таким образом, получаем следующее выражение для коэффициента использования СМО с l обслуживающими устройствами:

.

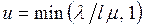Для СМО с одним обслуживающим устройством коэффициент использования 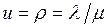, если 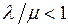, т.е. совпадает с нагрузкой.

При анализе моделей вычислительных систем одним из основных показателей качества служит пропускная способность. Эта величина как среднее число заявок, обслуженных за единицу времени. В СМО с l обслуживающими устройствами за каждую единицу времени в среднем завершается обслуживание 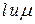заявок, откуда вытекает, что пропускная способность равна

.

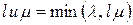Таким образом, пропускная способность совпадает с интенсивностью поступления заявок 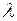до тех пор, пока 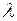меньше максимальной интенсивности обслуживания 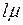, выше которой пропускная способность не поднимается.

С точки зрения заявки самым важным показателем качества, по-видимому, является время, которое она проводит в ожидании обслуживания. Определим время ожидания 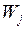заявки j,равным отрезку времени от начала поступления заявки j в систему до начала ее обслуживания, а время ответа 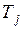– равным отрезку времени от момента поступления заявки j в систему до момента завершения ее обслуживания. Таким образом, имеем следующее простое соотношение (индекс j опущен):

Время ответа(T)=время ожидания(W)+длительность обслуживания(S)

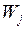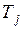Для оценки качества СМО обычно применяются средние значения случайных величин и в установившемся (стационарном) режиме, когда 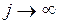. Эти средние уже не зависят от j, и мы будем обозначать их символам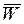и и 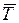соответственно.

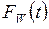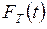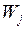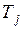Более подробную информацию о качестве СМО могут дать функции распределения и случайных величин и в установившемся режиме 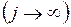. Примером, где такие распределения представляют интерес, может служить случай, когда заявка может покинуть систему, если задержки велики.

Последней интересующей нас мерой загруженности является длина очереди. Пусть случайный процесс 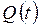есть число заявок, ожидающих обслуживания в момент времени t. Аналогично, определим 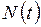как число заявок, находящихся в системе – либо в очереди, либо на обслуживании. Процесс 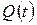называют длиной очереди. В СМО с l обслуживающими устройствам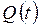и и 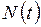связаны соотношением

.

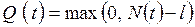Изучение распределения числа заявок, ожидающих обслуживания, требуется, например, при оценке объема буферной памяти, необходимой для размещения поступающих заявок.

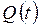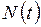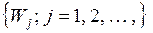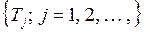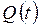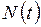Процессы и – это случайные процессы с непрерывным временем. Поэтому для оценки качества СМО, также как и в случае случайных последовательностей и , применяются средние значения случайных процессов и в установившемся режиме, когда 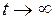. Эти средние уже не зависят от t, и мы будем обозначать их символам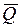и и 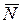соответственно.

Выведем (без излишней строгости) некоторые важные соотношения для показателей качества СМО 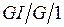в установившемся режиме. Пусть заданы 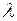– интенсивность поступления заявок в СМО и 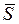– средняя длительность обслуживания заявки. Интенсивность обслуживания заявок работающим устройством есть 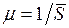, а интенсивность выходящего потока заявок в произвольный момент времени равна 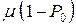, где 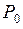– вероятность простоя обслуживающего устройства в установившемся режиме, т.е. 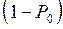– вероятность того, что устройство работает. Поскольку в установившемся режиме интенсивность ухода обслуженных заявок из системы совпадает с интенсивностью поступления заявок в систему, то 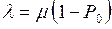. Отсюда

,

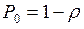где 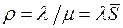– нагрузка, или коэффициент использования обслуживающего устройства. Как следует из (5), в установившемся режиме .

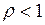ФОРМУЛА ЛИТТЛА

Теперь мы выведем одну важную формулу, связывающую (для предельного стационарного режима) среднее число заявок 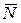, находящихся в системе массового обслуживания (т.е. обслуживаемых или стоящих в очереди), и среднее время пребывания заявки в системе 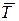. Рассмотрим любую СМО (одноканальную, многоканальную, марковскую, немарковскую, с неограниченной или ограниченной очередью) и связанные с ней два потока событий: поток заявок, прибывающих в СМО, и поток заявок покидающих СМО. Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее: оба потока имеют одну и ту же интенсивность .

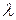Обозначим: 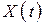– число заявок, прибывших в СМО до момента 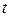, 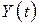– число заявок, покинувших СМО до момента 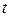. И та, и другая функция являются случайными и меняются скачком (увеличиваются на единицу) в моменты прихода заявок 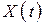и уходов заявок 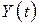. Вид функци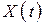й и 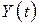показан на рисунке.

Обе линии – ступенчатые, верхняя – 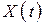, нижняя – 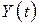. Очевидно, что для любого момента 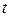их разность 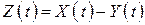есть не что иное, как число заявок, находящихся в СМО. Когда лини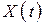и и 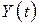сливаются, в системе нет заявок.

Рассмотрим очень большой промежуток времени 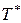(мысленно продолжив график далеко за пределы чертежа) и вычислим для него среднее число заявок, находящихся в СМО. Оно будет равно интегралу от функции 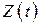на этом промежутке, деленному на длину интервала :

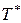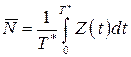. (1)

Но этот интеграл представляет собой не что иное, как площадь фигуры, заштрихованной на рисунке. Фигура состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки (первой, второй и т.д.). Обозначим эти времена 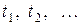. Правда, под конец промежутка 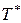некоторые прямоугольники войдут в заштрихованную фигуру не полностью, а частично, но при достаточно большом 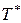эти мелочи не будут играть роли. Таким образом, можно считать, что

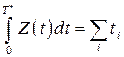, (2)

где сумма распространяется на все заявки, пришедшие за время .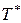

Разделим правую и левую части (2) на длину интервала 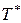. Получим с учетом (1),

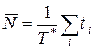. (3)

Разделим и умножим правую часть (3) на интенсивность l:

.

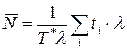Но величина 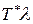есть не что иное, как среднее число заявок, пришедших за время 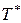. Если мы разделим сумму всех времен 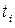на среднее число заявок, то получим среднее время пребывания заявки в системе 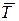. Итак

,

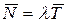Откуда

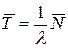. (4)

Это и есть формула Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.

Точно таким же образом выводится вторая формула Литтла, связывающая время пребывания заявки в очереди 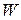и среднее число заявок в очереди :

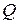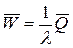. (5)

Для вывода достаточно вместо нижней линии на рисунке взять функцию 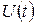– количество заявок, ушедших до момента 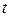не из системы, а из очереди (если заявка, пришедшая в систему, не становится в очередь, а сразу идет под обслуживание, можно все же считать, что она становится в очередь, но находится в ней нулевое время).