Интенсивность внутренних сил, передающихся через выделенную площадку, называется напряжением.

Понятие о деформациях и напряжениях.

Как элементы конструкций, так и конструкции в целом при действии внешних сил изменяют свои размеры и форму и, в конце концов, могут разрушиться. Это изменение носит название – деформация.

Деформация связана с физическими свойствами тела. Тело, под действием приложенных к нему сил деформируется, но после удаления нагрузки восстанавливает свою первоначальную форму.

Способность тела восстанавливать свою первоначальную форму после удаления внешних сил называется упругостью.

Но тело может и не восстановить свою первоначальную форму.

Деформации разделяются на упругие и остаточные.

Упругими деформациями называются такие изменения формы и размеров элементов, которые исчезают после удаления нагрузки – тело восстанавливает свою прежнюю форму. Эти деформации связаны с упругими искажениями решетки атомов.

Остаточными деформациями называются такие изменения формы и размеров элементов, которые не исчезают после удаления нагрузки. Эти деформации связаны с необратимыми перемещениями одних слоев кристаллической решетки относительно других.

Основными типами деформаций являются:

1.Растяжение – сжатие.

Растяжению – сжатию подвергаются стержни, вдоль осей, которых действует внешняя сила. При этом происходит поступательное перемещение поперечных сечений стержня.

2.Сдвиг.

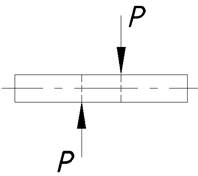Сдвиг возникает тогда, когда внешние силы смещают два параллельных плоских сечения одно относительно другого при неизменном расстоянии между ними.

Рис.2.1 Сдвиг.

3.Кручение.

Кручение возникает при действии на стержень внешних сил, образующих момент относительно оси стержня. Эта деформация сопровождается поворотом сечений стержня относительно друг друга.

4.Деформация изгиба заключается в искривлении оси прямого стержня или

изменения кривизны кривого стержня. Деформация изгиба прямого стержня характеризуется углом поворота сечений φ и прогибом У.

Эти четыре типа деформаций называются простыми.

В конструкциях встречается и более сложная работа элементов, когда они испытывают два, и более типов деформаций одновременно: растяжение с изгибом, изгиб с кручением и т.д. в этих случаях мы имеем дело с так называемой сложной деформацией.

Виды нагружения бруса.

1. Растяжение – сжатие

2. Изгиб

3. Кручение

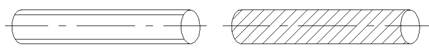
Рис. 2.2. Виды нагружения бруса.

Метод сечение

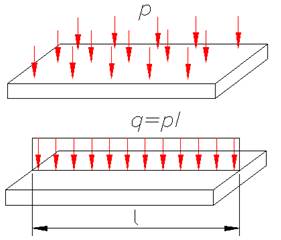
Равнодействующая распределенной нагрузки численно равна площади ее эпюры и приложена в центре ее тяжести.

Если нагрузка распределена по небольшой части поверхности, то ее заменяют сосредоточенной силой.

Между соседними частицами тела (молекулами, атомами) всегда имеются силы взаимодействия – внутренние усилия, называемыми внутренними силовыми факторами. Эти силы стремятся сохранить тело, препятствуют всякой попытке изменить взаимное расположение частиц, т.е. деформировать тело.

Величина внутренних сил в нагруженном и ненагруженном теле будет разной (пример). [В сопромате рассматривают только те дополнительные величины внутренних сил, которые появляются в результате нагружения тела]. Внутренние силы часто называют усилиями.

Для вычисления внутренних сил широко применяют метод сечений.

Порядок расчета:

1. Рассекаем тело плоскостью на 2 части

2. Отбрасываем одну из частей

3. Заменяем действие отброшенной части на оставленную, внутренними силами, распределенными по сечению

4. Заменим внутренние силы упругости главным вектором и главным моментом

5. Разложим главные векторы и главный момент внутренних сил на составляющие, которые называются внутренними силовыми факторами:

Nz - продольная сила – это сумма проекций всех внутренних сил в сечении на нормаль к сечению (на ось стержня).

Qx и Qy – перерезывающие силы - это сумма проекций всех внутренних сил в сечении на главные центральные оси сечения x и у.

Мz – крутящий момент это сумма проекций всех внутренних сил в сечении относительно оси стержня.

My , Mx – изгибающие моменты это сумма проекций всех внутренних сил в сечении относительно главных центральных осей сечения у и x.

6. Составим уравнения равновесия для пространственной системы сил, действующих на оставленную часть бруса.

Qx=ΣFx вн Qу=ΣFу вн Qz=ΣFz вн

Мх = Мх вн Му = Му вн Мz = Мz вн

Графики, показывающие, как изменяются усилия при переходе от сечения к сечению, называют эпюрами. (Построить эпюры N ,Q).

Напряжения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении.

Интенсивность внутренних сил, передающихся через выделенную площадку, называется напряжением.

Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц. Исследуя напряженное состояние тела в данной точке выделяют элемент в виде бесконечно малого параллелепипеда, так чтобы координатные оси направлены вдоль ребер и точка А совмещена с началом координат. Вырежем параллелепипед, длина ребер равна dZ и dY, а толщина равна 1.

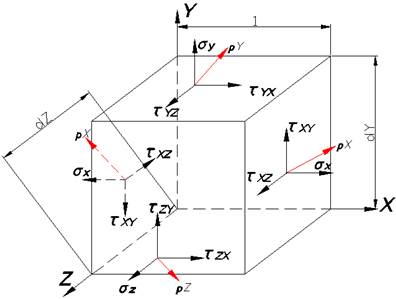
Рис. 2.3 Напряжение в точке тела.

К граням приложены внутренние силы, заменяющие воздействие удаленной части тела и направленные под углом к грани.

[Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении). Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши.]

Индексы обозначают нормаль к площадке, на которой действует напряжение. Полные напряжения на гранях элемента представляют нормальными и касательными составляющими - проекциями полных напряжений на координатные оси.

Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальные напряжения обозначают буквой σ с индексом, соответствующим направлению нормали к площадке, на которой они действуют, касательные напряжения обозначают буквой 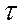с двумя индексами: первый соответствует направлению нормали к площадке, второй – направлению самого напряжения.

Сила, приложенная к какой-либо грани равна соответствующему напряжению, умноженному на площадь грани: 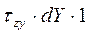.Нормальные силы на гранях параллелепипеда взаимно уравновешены. Касательные усилия образуют на тех же гранях две пары сил: τ_ZYdY с плечом dZ и τ_YZdZ с плечом dY, суммарный момент которых должен быть равен нулю.

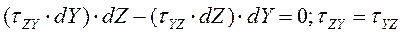
в виду того, что элементарный параллелепипед может быть ориентирован произвольно, это соотношение выражает общее положение, называемое законом парности касательных напряжений. Следствием этого закона является то, что на гранях выделенного элемента имеем не 9,а 6 компонентов напряжений, поскольку касательные напряжения попарно равны.

Продольная (осевая) сила в сечении является равнодействующей возникающих в каждой из точек сечения нормальных усилий.

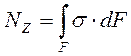
Возникают при растяжении – сжатии.

Перерезывающая сила в сечении является равнодействующей возникающих в каждой из точек сечения касательных усилий.

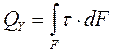
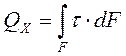
Касательные напряжения возникают при сдвиге (срезе).

Изгибающий момент (Мх и Му) – это равнодействующий момент, относительно нейтральной оси (х и у), всех внутренних нормальных сил, возникающих в поперечном сечении.

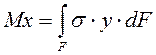
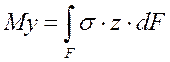
Крутящий момент (Мz) – это равнодействующий момент, относительно продольной оси (z) , всех внутренних касательных сил, возникающих в поперечном сечении

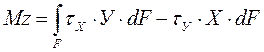
Эти зависимости используются для определения напряжений.

Зная внешние силы, с помощью метода сечений определяются внутренние силовые факторы, а затем напряжения по установленным зависимостям.

Иногда кроме нормальных и касательных напряжений рассматривают еще и полное напряжение.

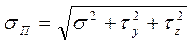
Пример крыла Обшивка растяжение – сдвиг.