Теплопроводность граней контрольного объема

В уравнении (5.2) коэффициент теплопроводности l_е был использован для обозначения l на грани е контрольного объема, соответственно l_w — на грани w. Если коэффициент теплопроводности является функцией х, будем знать l_е только в узловых точках W, P, Eи т.д. В этом случае необходимо каким-то образом определить коэффициент теплопроводности на грани контрольного объема, например определить l_е через значения коэффициентов теплопроводности в узловых точках.

Обсуждение, проведенное ниже, не имеет отношения к случаю постоянного коэффициента теплопроводности. Переменный коэффициент теплопроводности может быть результатом неоднородности материала (например, составные пластины).

Даже в однородном материале зависимость коэффициента теплопроводности от температуры может привести к его изменению, вызванному изменением температуры. В дифференциальном уравнении общего вида, записанном относительно Ф, коэффициент диффузии Г может изменяться аналогично коэффициенту теплопроводности l.

Существенные изменения Г встречаются довольно часто, например, при турбулентном течении, где Г может играть роль коэффициента турбулентной вязкости или теплопроводности. Таким образом, сама постановка задачи для переменного l или Г достаточно оправдана.

Наиболее простым способом определения коэффициента теплопроводности на грани контрольного объема является предположение о линейном изменении l между точками Р и Е. Пусть

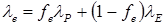, (5.4)

где 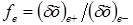— интерполяционный коэффициент, равный отношению отрезков, показанных на рисунке.

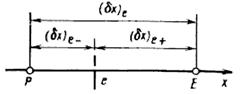
Если грань контрольного объема расположить посередине между узловыми точками, то 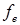будет равно 0,5 и l_е будет средним арифметическим l_P и l_E.

В дальнейшем покажем, что в некоторых случаях это простое приближение дает не совсем правильные выводы и не обеспечивает точной аппроксимации при резких изменениях коэффициента теплопроводности, что может иметь место в составных материалах. Имеется сравнительно простои способ, дающий лучшие результаты. Развивая этот способ, понимаем, что на самой грани контрольного объема е не существует локального значения коэффициента теплопроводности, которое нас интересует.

Основная цель данного рассмотрения — получение хорошего представления для теплового потока q_e на грани контрольного объема:

, (5.5)

которое в сущности используется в дискретном аналоге. Соотношение, определяющее l_е, следует выбрать так, чтобы получить правильное значение q_e.

Предположим, что контрольный объем, окружающий узловую точку Р, заполняет материал с постоянным коэффициентом теплопроводности l_P, а объем, окружающий точку Е,— материал с коэффициентом теплопроводности l_E.Для составной пластины с границей слоев, расположенной между точками Р и Е,для случая стационарной одномерной задачи (без источников теплоты) запишем

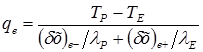(5.6)

Объединяя уравнения (5.4) — (5.6), получаем

(5.7)

Когда грань е расположена посередине между точками Ри Е,имеем 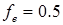, тогда

(5.7а)

Из уравнений (5.7) видно, что l_е представляет собой среднее гармоническое величин l_P и l_E,вместо среднего арифметического, которое дает уравнение (5.4) при .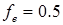

Эффективность этой формулировки видна из следующих двух предельных случаев.

1. Пусть l_E → 0, тогда l_е → 0.

Это означает, что тепловой поток на грани контрольного объема становится равным нулю, что и следовало ожидать. Выражение, представляющее собой среднее арифметическое, в этом случае будет давать ненулевое значение теплового потока.

2. Пусть l_P >> l_E, тогда .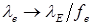

Из этого результата следуют два вывода, один из которых очевиден. Уравнение показывает, что коэффициент теплопроводности поверхности раздела l_е совершенно не зависит от l_P. Это вполне понятно, так как высокопроводящая среда, окружающая точку Р, должна иметь пренебрежимо малое сопротивление по сравнению со средой вокруг точки Е. Второй вывод заключается в том, что l_е не равно l_E, а больше этого значения в 1/f_e раз.

Рассмотрение этих двух предельных случаев показывает, что при использовании соотношения (5.7) можно аппроксимировать резкие изменения коэффициента теплопроводности, не применяя чрезмерно частой сетки.