Нелинейная регрессионная модель

Нелинейным называется уравнение вида y = ax^b

Линейная модель нашего примера :

ŷ= - 0,1678 + 2,0819x

Преобразуем ее с помощью логарифмирования и оценим:

y= - 0, 1678 +2, 0819 lnx

= * = 0,84 x^2,0819

Коэффициент при lnx представляет собой непосредственную оценку параметра 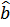. Полученный результат предполагает, что эластичность равна 2,0819, т.е.увеличение количества рабочих на 1% от среднего уровня приведет к увеличению объема перевозок на 2,08% от среднего уровня 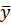. Коэффициент 0,84 помогает прогнозировать значения y при заданных значениях x, приводя их к единому масштабу.

В случае нелинейной регрессии степень концентрации распределения наблюдаемых точек вблизи линии регрессии показывает корреляционное отношение или индекс корреляции:

= = 0,806

Близость индекса корреляции к единице говорит о сильной связи между переменными.

Коэффициент детерминации R²=0,806² =0,649, то есть можно сказать, что 64,9% изменения объема перевозок обусловлено зависимостью количества человек, в то время как на все остальные факторы, не учтенные в уравнении регрессии, приходится 35,1%.

Сравнение

№	Модель	Уравнение	; rв	R2
	Линейная	у = а + bx	0,898	0,806
	Нелинейная	y = axb	0,806	0,649

В случае линейной модели коэффициент детерминации ближе к 1, т.е. качество регрессии лучше, более точно аппроксимирует у. Это довод в пользу линейной модели.

Близость индекса корреляции к единице свидетельствует о сильной связи между переменными, т.е. нелинейная модель в данной задаче является менее подходящей, чем линейная.

Исходя из вышесказанного, делаем вывод, что линейная модель более подходит для отражения зависимости между количеством рабочих на предприятии и объемом перевозок.