Байланыстар және олардың р-ялары. Б-р аксиомасы. Б-ң нег. түрлері
Статиканың негізгі ұғымдары
ТМ зерттеу объектілері ретінде материялық денелердің модельдері алынады, олар материялық нүкте (МН), МН жүейсі және абсолют қатты дене (АҚД).
МН деп қарастырылатын жағдайда өлшемдерін ескермеуге болатын материялық денені айтамыз, оның массасы нуктеде жинақталыды деп есептеледі. МН жүйесі деп орындары мен қозғалыстары өзара байланысқан МН жиынтығын айтамыз (мысалы, механизм). АҚД - кез келген нүктелері арасындағы қашықтықтары өзгермейтін дене. Шынында барлық денелер күштер әсерінің нәтижесінде өз өлшемдерін және формасын өзгертеді (дефомацияланады). Көбінесе сол деформациялар аз болғандықтан, денені абсолют қатты дене деп деформацияларды есепке алмауға болады.
Дененің тепе-теңдік немесе қозғалыс қалпы оның басқа денелермен өзара механикалық әрекеттенуіне тәуелді, өзара әрекеттенудің өлшемі ретінде күш келеді. Күш – вектор, ол сан шамасымен (модулімен), бағытымен және түсу нүктесімен сипатталады. Графикалық түрде күш бағытталған түзу кесіндісімен көрсетіледі. Күш бағыты бойындағы түзу күштің әсер ету сызығы деп аталады. Күшті үстіне сызық қойып, латын әліппесінің үлкен әрпімен белгілейміз, мысалы,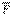 
, сонда F= 
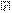- күштің модулі болады. Қатты денеге немесе нүктеге түсетін күштер жиынтығы күштер жүйесі (КЖ) деп аталады. Оны 
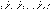арқылы белгілейміз.
Егер қатты денеге әсер ететін КЖ-н дененің тыныштық немесе қозғалыс қалпын өзгертпей, басқа КЖ-не ауыстыруға болса, олар баламалы күштер жүйелері деп аталады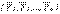 
~ 
.
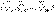Егер берілген КЖ бір ғана күшке баламалы болса, сол күш қарастырылып отырған КЖ-нің тең әсерлі күші (тең әсерлісі) деп аталады. Оны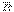 
* деп белгілесек, сонда 
*~ 
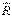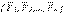. Кез келген КЖ-нің тең әсерлі күші бола бермейді.
КЖ денеге түскенде, ол дененің тыныштық немесе қозғалыс қалпын өзгертпейтін болса, КЖ теңгерілген деп аталады. Теңгерілген КЖ-нің әсері нөлге баламалы, яғни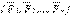 
~0. Егер күшті КЖ-не қосқанда, ол сонымен бірге нөлге баламалы жаңа КЖ-н құрса, оны КЖ-н теңгеретін күш деп атайды.
Дененің бір нүктесіне түсетін күш қадалған күш деп аталады. Дене көлемінің немесе бетінің бір бөлігінің барлық нүктелеріне түсетін күштер таралған күштер деп аталады.
Статика аксиомалары
Статика бірнеше аксиомаға негізделеді.
1. Екі күш жүйесінің тепе-теңдігі туралы аксиома. Денеге түсетін екі күш тепе-теңдікте болу үшін олардың шамалары тең болуы және түсу нүктелері арқылы өтетін түзу бойымен қарама-қарсы бағытталуы қажетті де, жеткілікті де: F1 = F2, бірақ 
(1.1 сурет).
2. Теңгерілген КЖ-н қосу және алып тастау аксиомасы. Күштер жүйесінің қатты денеге әсерін өзгертпей, соған теңгерілген КЖ-н қосуға немесе алып тастауға болады. Салдары: АҚД-ге түсетін күштің әсерін өзгертпей, оны әсер ету сызығы бойымен дененің кез келген басқа нүктесіне көшіруге болады (1.2 сурет), яғни күш - 
жылжымалы вектор.
3. Күштер параллелограмы аксиомасы. Өзара бұрыш құрып, бір нүктеге түсетін екі күштің тең әсерлісі сол күштер қабырғалары болып табылатын параллелограмның диагоналі ретінде анықталады (1.3 сурет), яғни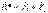 
.
4. Өзара әрекеттену аксиомасы. Екі дене бір-біріне шамалары тең және бір түзу бойымен қарама-қарсы бағытталған күштермен әсер етеді:
F21 = F12,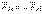 
.
Еркін емес дене үшін келесі аксиома орын алады.
5. Байланыстар аксиомасы. Еркін емес денені, байланыстарды алып тастап және олардың әсерін реакциялармен ауыстырып, еркін дене ретінде қарастыруға болады.
6. Қатаю аксиомасы. Деформацияланатын дененің КЖ-нің әсерінен болған тепе-теңдік қалпы, оған қосымша байланыстарды орнатса, тіпті денені қатайған (абсолют қатты) дене ретінде қарастырса да, өзгермейді.
Үш күш туралы теорема: егер дене бір жазықтықта орналасқан үш параллель емес күш әсерінен тепе-теңдік қалпында болса, онда сол күштердің әсер ету сызықтары бір нүктеде қиылысады.
Дәлелдеу: Дене үш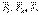 
күштері әсерінен тепе-теңдікте дейік. Олар параллель емес және бір жазықтықта болғандықтан, екі 
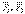күштерінің әсер ету сызықтары қиылысады, сонда күштерді сол нүктеге көшіріп, тең әсерлі 
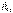күшіне ауыстыруға болады. Енді 
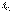күші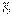 
күшін теңгереді, сондықтан олардың әсер ету сызықтары түйіседі, яғни барлық үш күштердің әсер ету сызықтары бір нүктеде қиылысады.
Байланыстар және олардың р-ялары. Б-р аксиомасы. Б-ң нег. түрлері.
Егер дененің кеңістікте кез келген орын ауыстыру алуға мүмкіншілігі болса, ол еркін дене деп аталады. Егер кейбір орын ауыстырулар мүмкін емес болса, дене еркін емес деп аталады. Дене қозғалысының еркіндігін шектейтін шарттар байланыстар деп аталады. Байланыстар қатты немесе икемді материялық денелер арқылы орындалады. Дене түскен күштер әсерінен байланыс кедергілік жасап тұрған орын ауыстыруды орындауға тырысып, оған күш түсіреді. Біржолы байланыс та денеге модулі тап сондай, бірақ қарама-қарсы бағытталған байланыстың реакциясы деп аталатын күшті түсіреді. Реакциялардан басқа күштерді актив (пәрменді) күштер деп атаймыз. Байланыс реакциясының актив күштерден айырмашылығы – оның шамасы актив күштерге тәуелді және алдын ала белгісіз. Реакцияның бағыты - байланыс дененің қозғалысына кедергілік жасайтын бағытқа қарама-қарсы. Кейбір байланыстардың (тіректердің) реакциялары қалай бағытталатынын қарастырайық:
а) абсолют тегіс бет (үйкелісті ескермеуге болады) дененің бет үстінде жылжуына кедергілік жасамайды, ол тек қана бетке тік бағытпен қозғалуға кедергілік жасайды. Сондықтан оның реакциясы жанасып тұрған денелердің беттеріне ортақ нормаль бойымен бағытталады және жанасу нүктесіне түседі;
б) икемді жіп немесе шынжыр. Мұнда реакция жіп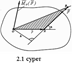 
немесе шынжыр бойымен бағытталады;
в) цилиндрлік топса (подшипник) немесе жылжымайтын топсалы тұғыр. Тесіктерінен өтетін білікпен қосылған екі дене топсалы (шарнирлі) қосылысты құрайды. Біліктің өстік сызығы топсаның өсі деп аталады. Дене топса өсіне перпендикуляр бағытта орын ауыстыра алмайды, бірақ ол өске қатысты айнала алады. Сондықтан реакция топса өсіне перпендикуляр жазықтықта кез келген бағытталуы мүмкін. Әдетте оны екі құраушы күшке жіктейді;
г) каток түріндегі тірек, яғни жылжымалы топсалы тұғыр. Үйкеліс күші ескерілмесе, реакция домалау бетінің нормалі бойымен бағытталады;
д) сфералық топса және өкшелік. Мұндай байланыс дененің бір нүктесі ешқандай орын ауыстыру ала алмайтындай қылып бекітеді, ал сол нүктеге қатысты дене кеңістікте кез келген бағытта айналуы мүмкін. Реакция бекітілген нүкте арқылы өтеді; оның бағыты алдын ала белгісіз болғандықтан, оны үш құраушы күшке жіктейді;
е) екі шетінде топсалармен бекітілген, салмағы ескерілмейтін сырық. Сырыққа топсалардың центрлерінде түсетін тек екі күш ғана әсер етеді. Сырық тепе-теңдікте болғандықтан, сол күштер (реакциялар) топсалардың центрлерінен өтетін түзу бойымен бағытталу керек.
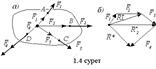3. Тоғысатын күштер жүйесі.
Күштер жүйелері (КЖ) келесі түрлерге бөлінеді: тоғысатын КЖ, параллель күштер жүйесі, кез келген КЖ. Тоғысатын деп күштердің әсер ету сызықтары (ӘС) бір нүктеде қиылысатын КЖ-ні атайды. Параллель деп, ӘС өзара параллель КЖ-ні атайды. Кез келген деп ӘС қиылыспайтын және параллель емес КЖ-сі аталады. Аталған КЖ жазық және кеңістік болуы мүмкін. Егер барлық күштердің ӘС бір жазықтықта жатса, КЖ жазық деп, керісінше жағдайда кеңістік деп аталады.
Дененің А, В, С, D нүктелерінде әсер ету сызықтары О нүктеде қиылысатын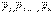 
күштері түседі дейік (1.4,а сурет). Күштерді олардың ӘС бойымен О нүктеге көшіріп, оларды тізбектеп күштер үшбұрышы ережесімен қосамыз (1.4 б сурет). Алдымен 
, 
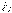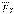күштерінің тең әсерлі 
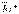күшін, сонан соң 
, 
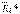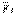күштерінің тең әсерлі 
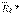күшін, сөйтіп т.б. табамыз. Сонда: 
, 
, 
= 
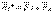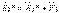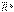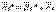. Күштер саны n болса, онда 
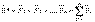(1.1)
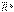күшін былай да табуға болады: алдымен 
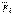векторын тұрғызып, оның ұшынан 
векторын,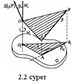 
содан кейін 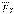векторының ұшынан 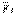векторын және сөйтіп т.б. тұрғызамыз. Сонда тең әсерлі 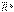күші бірінші вектордың басын соңғы вектордың ұшымен қосады. Сонымен, тоғысатын КЖ-нің тең әсерлі күші жүйедегі күштердің векторлық қосындысына тең. Оның ӘС күштердің ӘС қиылысу нүктесінен өтеді. Тең әсерлі күшін геометриялық тәсілімен табу үшін күштердің қиылысу нүктесінде күш көпбұрышын тұрғызу керек; оның тұйықтаушысы тең әсерлі күші болып келеді.
Тоғысатын КЖ-нің тең әсерлі күшін аналитикалық тәсілмен анықталуын қарастырайық. Ол үшін (1.1) векторлық теңдеуінің декарт координат жүйесінің өстеріне проекцияларын жазып, тең әсерлі күшінің проекцияларын анықтаймыз
, 
, 
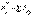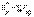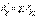. (1.2)
Тең әсерлі күшінің модулі келесі формуламен табылады
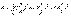(1.3)
ал оның бағыты – үш бағыттаушы косинустар арқылы табылады
, 
, 
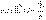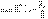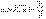. (1.4)
4. Тоғысатын күштер ж-ң векторлық, геометриялық, аналитикалық тепе теңдік шарттары. Тоғысатын КЖ тепе-теңдік қалпында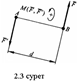 
болуы үшін оның тең әсерлі күші нөлге тең болуы қажетті де, жеткілікті де, яғни 
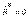немесе 
(тепе-теңдік шартының векторлық түрінде жазылуы). Тепе-теңдіктің геометриялық шарты – күш көпбұрышы тұйықталу керек, яғни соңғы күш векторының ұшы бірінші вектордың басымен түйісу керек. Тепе-теңдіктің аналитикалық шарттары - жүйедегі барлық күштердің үш координаттық өстеріне проекцияларының қосындылары нөлге тең болуы
, 
, 
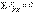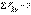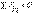. (1.5)
Тоғысатын жазық КЖ-нің тепе-теңдік шарттары мына түрде жазылады
, 
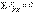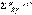. (1.6)