Площадь поверхности и объём шара
Пусть V – объём шара радиуса R, а S – площадь его поверхности. Заполнить таблицу.
| А) | Б) | В) | Г) | Д) | Е) | |
| R | 4см | 2,5см | 0,75м | |||
| S | 64 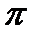 см2 см2 | 12см2 | ||||
| V | 113,04см3 |
РАБОТА № 57
Площадь поверхности и объём тел вращения
Пусть R- радиус, l- образующая,D- диаметр,H- высота, V- объём, S– площадь поверхности
| R | l | D | H | Sосн. | Sполн. пов. | V | |
| конус | а | в | |||||
| конус | с | Р | |||||
| конус | в | А | |||||
| конус | 25 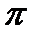 | ||||||
| цилиндр | в | А | |||||
| цилиндр | С | 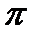 р2 р2 | |||||
| цилиндр | а | В | |||||
| цилиндр | с | Р | |||||
| шар | Нет | а | Нет | Нет | |||
| шар | Нет | Нет | Нет | 100 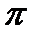 | |||
| шар | с | Нет | Нет | Нет | |||
| шар | Нет | Нет | Нет | 36 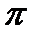 |
КОНТРОЛЬНАЯ РАБОТА № 1
Действительные числа
| Вариант № 1 | Вариант № 2 |
| 1) Вычислите: | |
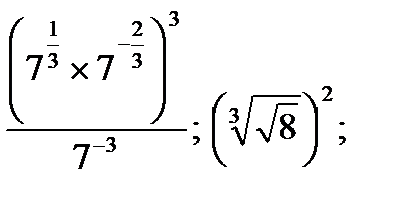 | 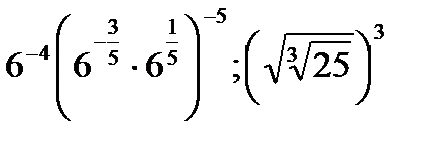 |
| 2) Упростите выражение | |
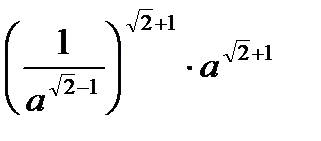 ; ; | 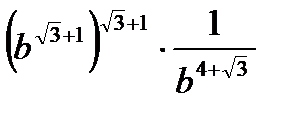 |
| 3) Решите уравнение: | |
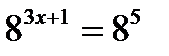 | 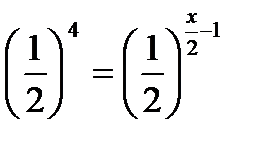 |
| 4*) Записать бесконечную периодическую дробь 0,(43) [0,3(6)] в виде обыкновенной дроби. | |
| 5*) Сократите дробь: | |
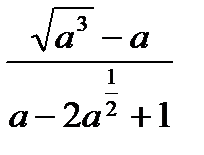 ; ; | 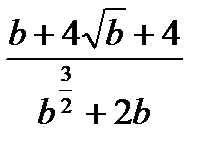 |
| 6*) Сравните числа: | |
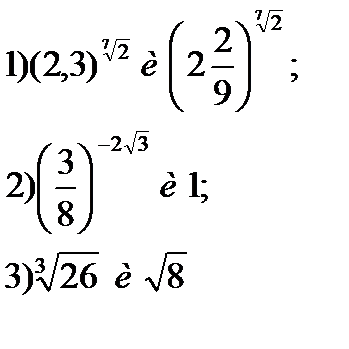 | 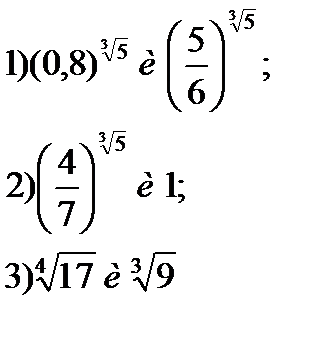 |
КОНТРОЛЬНАЯ РАБОТА № 2
Степенная функция
Вариант №1 Вариант № 2
1) Найти ООФ:
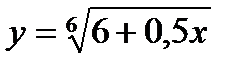
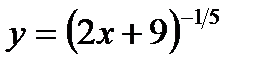
2) Изобразить эскиз графика функции 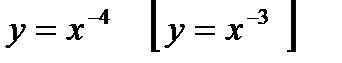 и перечислить её основные свойства. Пользуясь свойствами этой функции:
и перечислить её основные свойства. Пользуясь свойствами этой функции:
1)сравнить с единицей 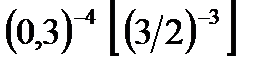
2)сравнить 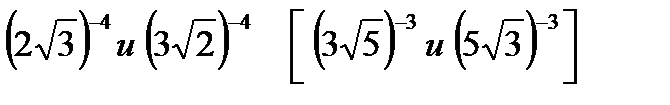
3) Решить уравнения:
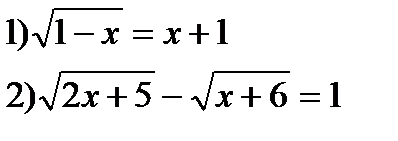
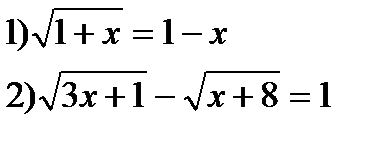
4*) Установить, равносильны ли неравенства:
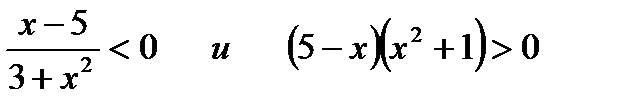 ;
;
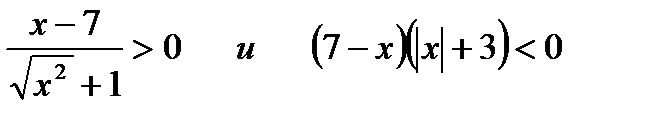
5*) Решить неравенство:
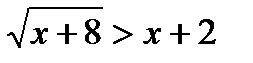
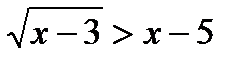
6*) Найти функцию, обратную данной 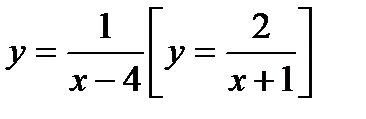 ; найти её область определения и множество значений.
; найти её область определения и множество значений.
КОНТРОЛЬНАЯ РАБОТА № 3
Показательная функция
Вариант № 1 Вариант № 2
1) Сравнить: 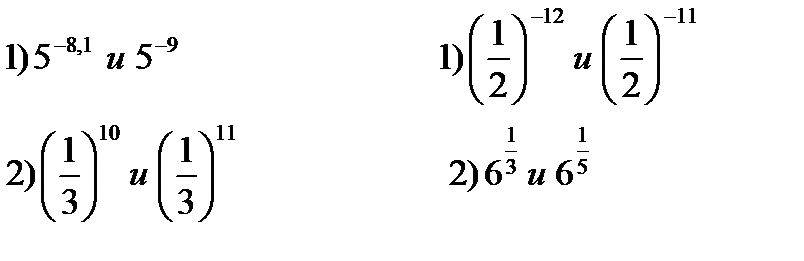
2) Решить уравнения:
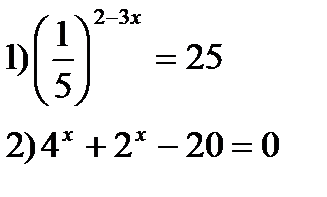
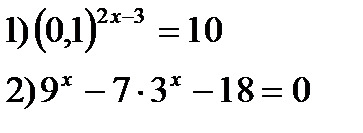
3)Решить неравенства:
4) 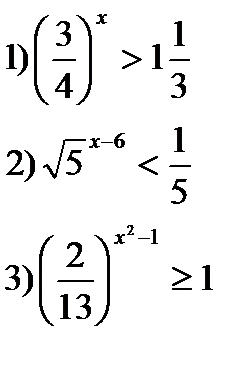
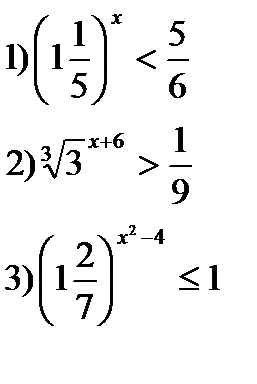
4*) Решить систему уравнений: 
5*) Решить уравнение:
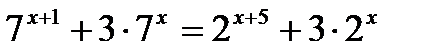
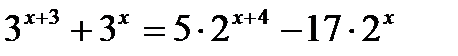
КОНТРОЛЬНАЯ РАБОТА № 4
Логарифмическая функция
Вариант № 1 Вариант № 2
1) Вычислить:
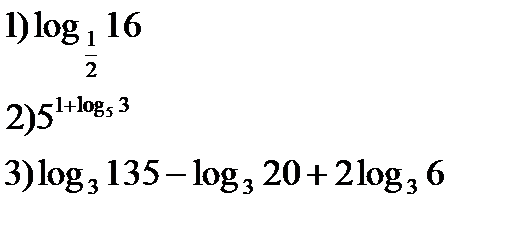
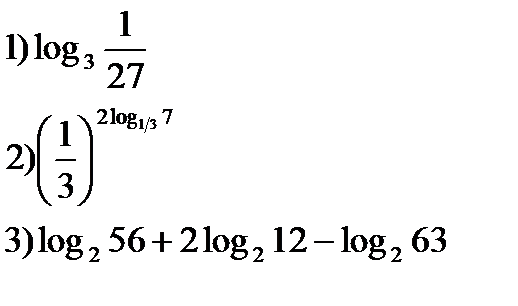
3) Сравнить:
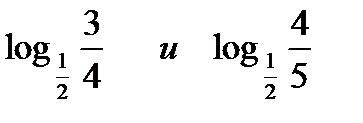
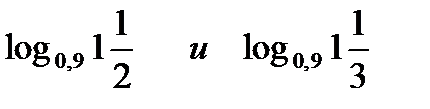
5) Решить уравнение:
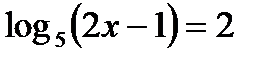
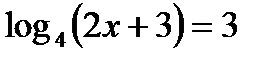
6) Решить неравенство:
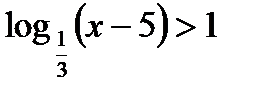
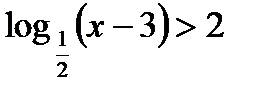
5*) Решить уравнение:
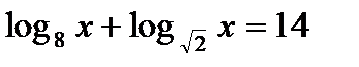
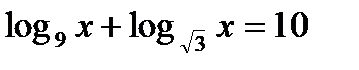
6*) Решить неравенство:
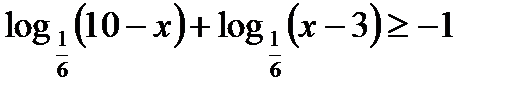
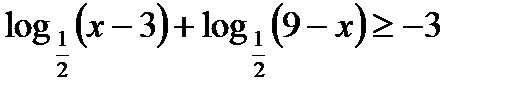
7*) Решить неравенство:
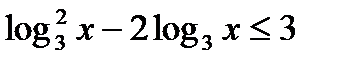
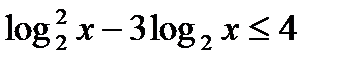
КОНТРОЛЬНАЯ РАБОТА № 5
Тригонометрические формулы
Вариант № 1 Вариант № 2
1) Вычислить:
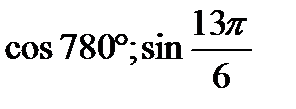
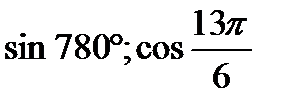
2) Найти:
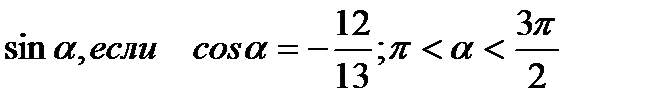 ;
;
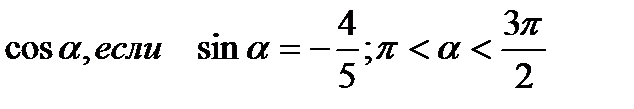
3) Упростить:
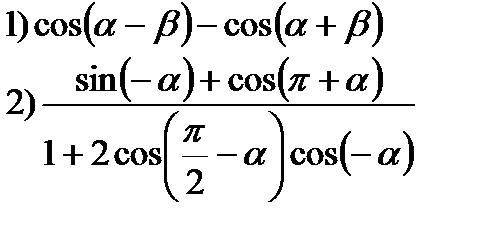
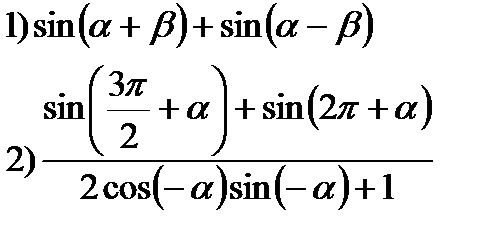
4*) Решить уравнение:
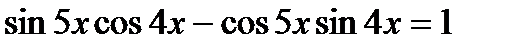 ;
;
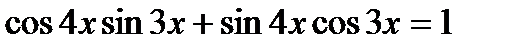
5*) Доказать:
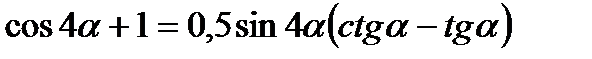 ;
;
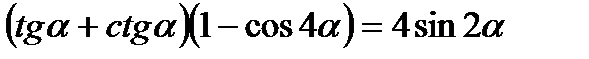
КОНТРОЛЬНАЯ РАБОТА № 6
Тригонометрические уравнения
Вариант № 1 Вариант № 2
1) Решить уравнения:
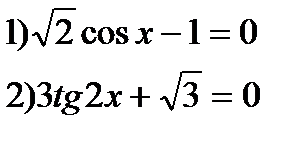
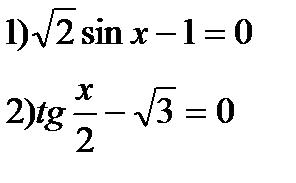
2) Найти корни уравнения
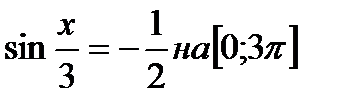
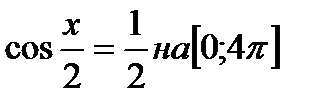
3) Решить уравнения:
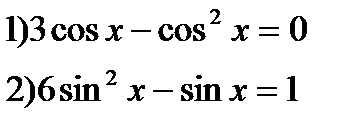
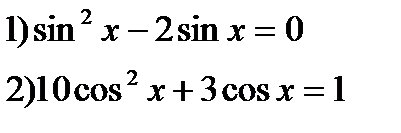
4*) Решить уравнения:
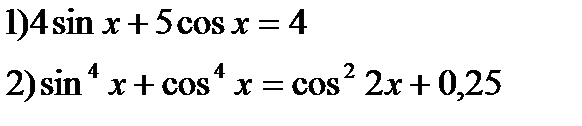
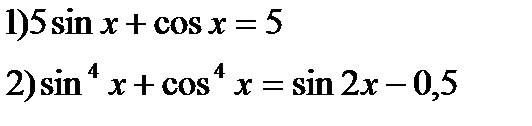
КОНТРОЛЬНАЯ РАБОТА № 7
Тригонометрические функции
Вариант № 1 Вариант № 2
1) Найти область определения и множество значений функции 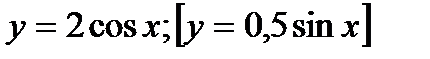
2) Выяснить, является функция 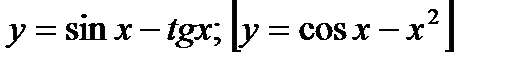 чётной или нечётной.
чётной или нечётной.
3) Изобразить схематически график функции 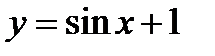 ;
; 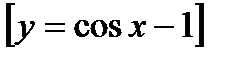 на
на 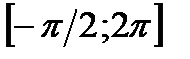
4*) Найти наибольшее и наименьшее значения функции: 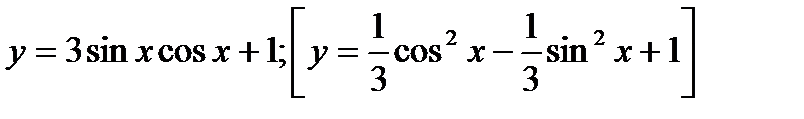
5*) Построить график функции
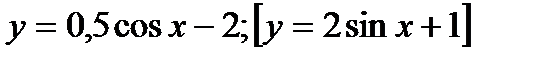 .
.
При каких значениях х функция возрастает [убывает]?
КОНТРОЛЬНАЯ РАБОТА № 8
Производная
Вариант № 1 Вариант № 2
1) Найти производные функций:
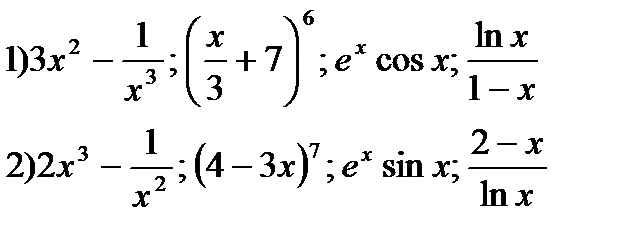
2) Найти значение производной функции f (х) в точке хо, если 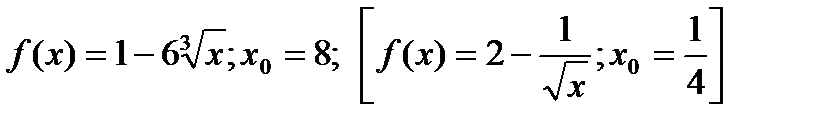
3) Написать уравнение касательной к графику функции 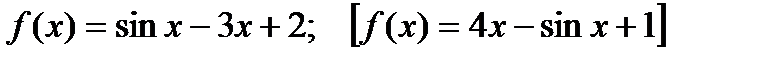 в точке с абсциссой хо= 0
в точке с абсциссой хо= 0
4*) Найти значения х , при которых значения производной функции 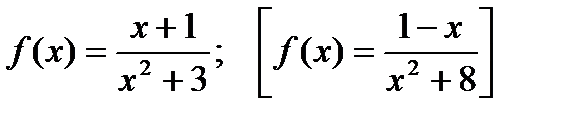 положительны [отрицательны].
положительны [отрицательны].
5*) Найти точки графика функции 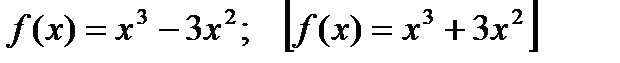 , в которых касательная к нему параллельна оси абсцисс.
, в которых касательная к нему параллельна оси абсцисс.
КОНТРОЛЬНАЯ РАБОТА № 9
Производная
Вариант № 1 Вариант № 2
1) Найти экстремумы функции
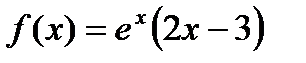
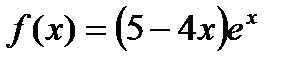
2) Найти интервалы возрастания и убывания функции 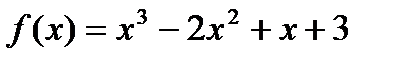
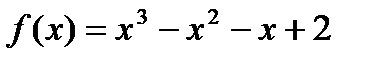
3) Построить график 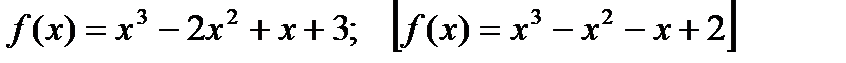 на [-1; 2]
на [-1; 2]
4*) Найти наименьшее и наибольшее значения функции 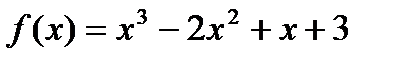 на [0; 1,5]
на [0; 1,5]
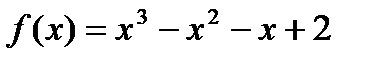 на [-1; 1,5]
на [-1; 1,5]
5*) 1)Среди прямоугольников, сумма длин двух сторон у которых равна 20, найти прямоугольник наибольшей площади.
2) Найти ромб с наибольшей площадью, если известно, что сумма длин его диагоналей равна 10.
КОНТРОЛЬНАЯ РАБОТА № 10
Первообразная
Вариант № 1 Вариант № 2
1) Доказать, что функция 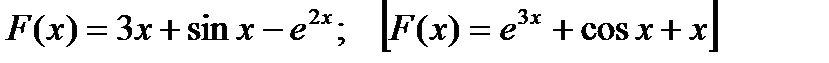 является первообразной функции
является первообразной функции 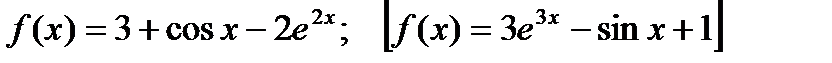 .
.
2) Найти первообразную F(x) функции 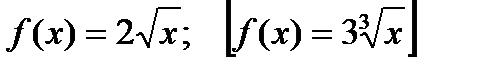 , график которой проходит через точку
, график которой проходит через точку 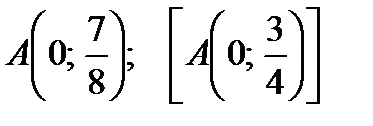
3) Вычислить площадь фигуры, ограниченной линиями 1)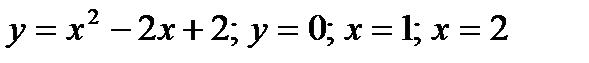
1)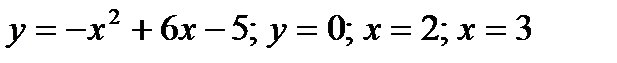
2*)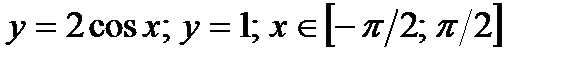
2*)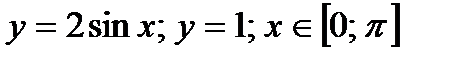
4*) Найти корни первообразной для функции
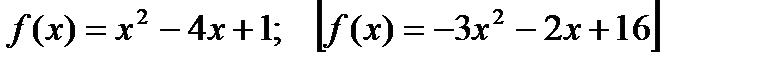 , если один из них равен 2[-1].
, если один из них равен 2[-1].
Литература
1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10 - 11 Кл. - М.: Просвещение.
2. Батанова А. Фрагмент урока на тему " Предметы и их формы" // Математика, 2009, № 23.
3. Виленкин Н.Я. и др. За страницами учебника математики 10-11 класса.- М.: Просвещение, 1996.
4. Высоцкий И. Р. и др. ЕГЭ 2011. Математика. Универсальные материалы для подготовки учащихся / ФИПИ – М.: Интеллект-центр, 2011. стр. 83-86.
5. Глейзер Г.И. История математики в школе. VII-VIII классы. Пособие для учителей. М.: Просвещение, 1982.
6. Земляков А.Н. Геометрия в 11 классе. Методические рекомендации к учебнику А.В. Погорелова. М.: Просвещение, 2003.
7. Иванова О. Многогранники вокруг нас //Математика, 2005, № 3.
8. Погорелов А.В. Геометрия. Учебник для 10-11 классов общеобразовательных учреждений Т.Л. Афанасьева, Л.А. Тапилина. Геометрия. 11 класс. (Поурочные планы). Волгоград. Издательство “Учитель”, 1999. М.: Просвещение, 2005.
9. Скворцова Н. В. Учась - твори! Нетрадиционные формы проведения уроков математики. - Йошкар-Ола. Педагогическая инициатива, 2003.
10. Формирование опыта творческой деятельности в процессе обучения математике [Текст] /авт.-сост. В. И. Маркова. - Киров: КИПК и ПРО, 2009. – 156 с.
11. Ященко И. В., Шестаков С. А., Захаров П. И. Подготовка к ЕГЭ по математике в 2011 году, методические указания. – М.: МЦНМО, 2011. стр.15-16, 74-78.
