Регулярні мови і регулярні вирази

Лема Ардена

Нехай A i B – двi мови, причому , i мова X задовольняє рiвнiсть X = AX∪B. ТодiX = .

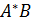Дов. Доведемо за iндукцiєю, що X⊂ 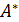B. Спершу, розглянемо випадок ω = e. Якщо ω∈X, то ω∈AX∪B. Оскiльки , то необхiдно ω∈Bi, отже, ω∈ 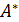B. Далi, припустимо, що для всiх слiв ω довжини менше n виконується, що якщо ω∈X, то ω∈ 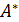B, i розглянемо слово α довжини n. Якщо α∈X = AX∪B, то, або α∈B⊂ 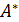B або

α = βγ для деяких β∈Aiγ∈X. В другому випадку мусить виконуватися β 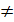ei, отже,

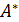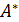|γ| < |α|. Отже, за iндуктивним припущенням, γ∈ Biα∈A B⊂ 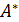B. Цим завершується iндуктивний крок i, отже, X⊂ 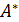B.

Щоб довести протилежне включення, використаємо iндукцiю, щоб показати, що 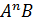⊂X для всiх n ≥ 0. Для n = 0, ми маємо, що 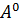B = B⊂AX∪B = X. Для n> 0 за індуктивним припущенням виконується 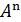B = A( 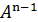B) ⊂AX. Таким чином,

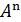B⊂AX⊂AX∪B = X. Дов.

Регулярні мови і регулярні вирази.

Нехай X – довiльний алфавiт. Визначимо регулярну мову (множину) в алфавiтi X рекурсивно наступним чином:

1) порожня множина ∅ є регулярною мовою;

2) для кожної букви a ∈ X множина {a} є регулярною мовою;

3) якщо A i B є регулярними мовами, то множини A ∪ B, AB і 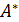також є регулярними мовами;

4) iнших регулярних мов не iснує.

Пpиклад.

1) множина {e} є регулярною мовою, бо {e} = ;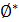

2) множина {001, 110} – регулярна мова над бiнарним алфавiтом, бо

{001, 110} = ({0}{0}{1}) ∪ ({1}{1}{0});

Щоб спростити зображення регулярних мов, визначимо поняттярегулярного виразу над алфавiтом X наступним чином:

1) порожня множина ∅ є регулярним виразом, який позначає порожню множину;

2) e є регулярним виразом, який позначає мову {e};

3) для кожної букви a ∈ X a – регулярний вираз, що позначає мову {a};

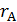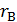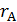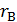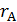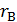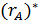4) якщо i є регулярними виразами, що позначають мови A i B вiдповiдно, то ( )+( ), ( )( ) i є регулярними виразами, що позначають мови A ∪ B, AB i 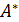вiдповiдно;

5) iнших регулярних виразiв над алфавiтом X не iснує.

Щоб зменшити кiлькiсть дужок в регулярних виразах, будемо вважати, що найвищий прiоритет має операцiя iтерацiї ∗, потiм – конкатенацiя i останньою виконується операцiя +. Наприклад, 01 позначає {01}, 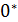– 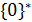, – 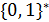, а 001 позначає

множину всiх слiв, якi складаються з нулiв i одиниць i закiнчуються словом 001.

Для кожної регулярної мови iснує нескiнченно багато виразiв, що ї ї зображують. Наприклад, вирази 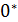1+∅ i 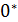1 зображують одну й ту ж мову 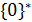{1}. Кажемо, що

два регулярних вирази рiвнi (=), якщо вони позначають одну i ту ж

множину.

3.2. Твеpдження. Нехай α, β i γ – регулярнi вирази. Тодi:

• α + β = β + α; • 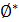= e; • α + (β + γ) = (α + β) + γ; • α(βγ) = (αβ)γ; • α(β + γ) = αβ + αγ;

• (α + β)γ = αγ + βγ; • αe = eα = α; • ∅α = 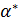α∅ = ∅; • = α + 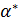; • 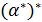= 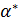; • α + α = α;

• α + ∅ = α.

Доведення. Нехай α i β позначають множини A i B вiдповiдно. Тодi α+β позначає A∪B, а β +α позначає B ∪A. Але A∪B = B ∪A за означенням об’єднання, тому α + β = β + α. Решту рiвностей доводяться аналогiчно. Дов.

Для зручностi запису введемо таке позначення: = .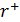

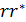Регулярнi вирази часто зображують помiченими орiєнтованими графами, стрiлки яких позначають буквами з алфавiту X ∪ {e}. Для довiльного регулярного виразу r, граф, що його зображує, утворюється наступним чином:

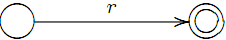Спочатку малюємо двi спецiальнi вершини, якi називаються початковою i кiнцевою вершинами, i сполучаємо їх стрiлкою, позначеною r:

Далi, повторюємо наступнi кроки, доки кожна позначка довiльної стрiлки не мiститиме символiв +, · :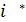

1)замiнюємо кожну стрiлку з позначкою f +g на двi паралельнi стрiлки з позначками f i g:

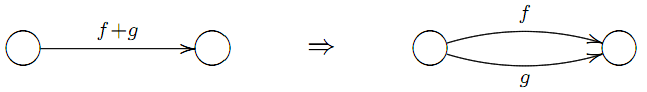
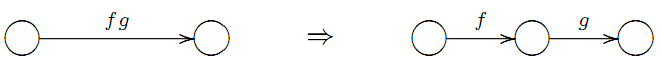2) замiнюємо кожну стрiлку з позначкою fg на додаткову вершину i двi стрiлки з позначками f i g:

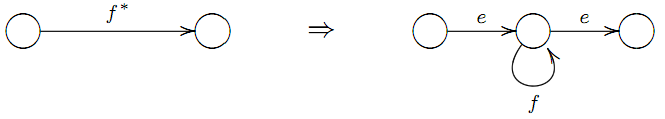3) замiнюємо кожну стрiлку з позначкою 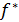на додаткову вершину i на три стрiлки з позначками e, f i e:

Для регулярного виразу r позначимо через G(r) помiчений орiєнтований граф, що його зображує. Очевидно, що кожна стрiлка в G(r) має позначку з множини X ∪ {e}. Кожному шляху в G(r) вiдповiдає слово, яке одержується конкатенацiєю всiх букв, якi позначають стрiлки шляху. Слово x належить мовi L(r) тодi i тiльки тодi, коли iснує шлях в G(r) з початкової вершини в кiнцеву вершину, якому вiдповiдає слово x. Кожна

е - стрiлка в G(r), яка є єдиною вихiдною стрiлкою з некiнцевої вершини чи єдиною вхiдною стрiлкою в непочаткову вершину може бути стягнута в одну вершину.

3.Формальні породжувальні граматики.Типи граматик.

Ієрархія Хомскі. Дерево виводу.

Формальною породжувальною граматикою називається четвірка виду G = (N, T, S, P), де N – скiнченна непорожня множина, елементи якої будемо називати нетермiнальними символами, T – скінченна непорожня множина, елементи якої будемо називати термiнальними символами, S ∈ N – початковий нетермiнальний символ, P – скiнченна множина продукцiй (правил перетворення) вигляду ξ → η, де ξ та η – слова в алфавiтi

N ∪ T. Букви термiнального алфавiту позначатимемо малими латинськими буквами чи цифрами, а нетермiнального алфавiту – великими латинськими буквами. Слова в алфавiтi N ∪T, як завжди, будемо позначати малими грецькими буквами. Нагадаємо, що множину всiх слiв в алфавiтi A позначають через .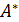

Нехай G = (N, T, S, P) – граматика, i нехай 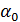= σ ξ τ (тобто 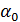– конкатенацiя слiв σ, ξ i τ ), 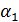= σ η τ – слова в алфавiтi N ∪ T. Якщо ξ → η – продукцiя граматики G, то говорять, що 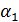безпосередньо виводиться з 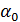, i записують 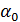⇒ 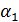. Якщо 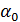, , 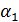. . . , 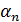– слова в алфавiтi N ∪ T такi, що 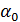⇒ ⇒ 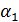⇒ . . . ⇒ ⇒ 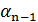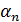, то говорять, що 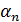виводиться з 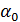i записують .

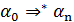Мовою, що породжується граматикою G = (N, T, S, P), називають множину всiх слiв термiналiв, якi виводяться з початкового символу S. Її позначають L(G). Таким чином, L(G) = {ω ∈ T∗| S ⇒∗ω}.

Якщо ми маємо багато правил граматики з однаковими лівимичастинами

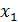A → ,A → 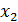, . . .A → 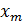, то ми можемо об’єднати їх в одне правило наступного вигляду A → | | . . . | .

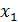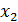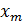Граматики класифiкують за типами продукцiй. Розглянемо класифiкацiю, яку запропонував американський математик i лiнгвiст Н.Хомскi. Принцип цiєї класифiкацiї полягає в тому, що на продукції накладено певнi обмеження. Вiн подiлив граматики на чотири типи.

У граматицi типу 0 немає жодних обмежень на продукцiї. Граматика типу 1 може мати продукцiї лише у виглядi ξ → η, де довжина слова η не менша, нiж довжина слова ξ, або у виглядi ξ → e. У граматицi типу 2 можуть бути лише продукцiї A → ω, де A – нетермiнальний символ, ω ∈ 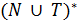. Граматика типу 3 може мати такi продукцiї:

A → ωB, A → ω i A → e, де A, B – нетермiнали, ω – слово з термiналiв. Iз цих означень випливає, що кожна граматика типу n, деn = 1, 2, 3, є граматикою типу n−1. Граматики типу 2 називають контекстно вiльними, бо нетермiнал A в лiвiй частинi продукції

A → η можна замiнити словом η в довiльному оточеннi щоразу, коли він зустрiчається, тобто незалежно вiд контексту.

Мову, яку породжуєграматика типу 2, називають контекстно вiльною. Якщо в множинi продукцiй P є продукцiя виду γ µ δ → γ ν δ, |µ| ≤ |η|, то граматику називають граматикою типу 1, або контекстно залежною, оскiльки µ можна замiнити на ν лише в оточеннi слiв γ . . . δ, тобто у вiдповiдному контекстi. Мову, яку породжує граматика типу 1, називаютьконтекстно залежною. Граматику типу 3 називають праволiнiйною.

Двоїсто визначають лiволiнiйну граматику – вона може мати такi продукцiї:

A → ωB, A → ω i A → e, де A, B – нетермiнали, ω – словоз термiналiв. Лiволiнiйнi i праволiнiйнi граматики називаються регулярними. Регулярнi граматики породжують регулярнi мови i тількиїх.

Слово ω належить мовi L(G) контекстно вiльної граматики G тодi i лише тодi, коли iснує виведення S 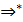ω в G. Таке виведення показує як крок за крококом застосовуються продукцiї граматики, щоб одержати слово ω з початкового нетермiнального символу S.

Це виведення можна також продемонструвати наочно з допомогоюдерева, яке називатемемо деревом виведення. Наприклад, розглянемо контекстно вiльну граматику G = ({S}, {a, b, c}, S, P), де P = {S →SbS | ScS | a} i слово abaca ∈ L(G). Виведення

S ⇒ SbS ⇒ SbScS ⇒ abScS ⇒ abSca ⇒ abaca показано на рисунку (а), а виведення

S ⇒ ScS ⇒ SbScS ⇒ abScS ⇒ abSca ⇒ abaca зображено деревом на рисунку (б).

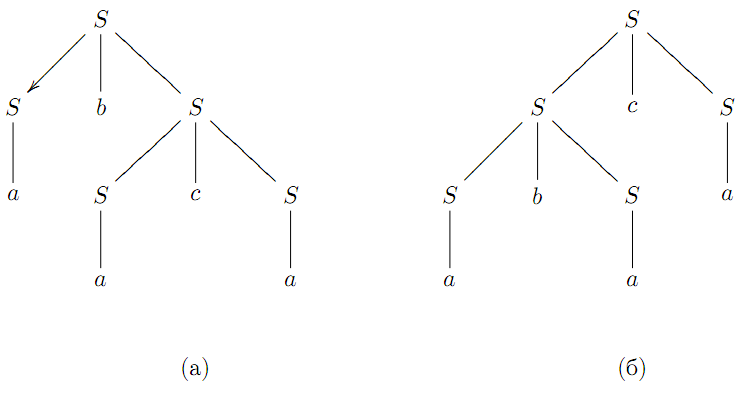
В загальному випадку для контекстно вiльної граматики G =(N, T, S, P) дерево виведення будується наступним чином:

1) Вершиною дерева є початковий нетермiнальний символ S.

2) Повторюємо наступнi кроки доти, доки кожен листок дерева буде або порожнiм символом e або термiнальним символом: длякожного листка A ∈ N дерева обираємо продукцiю A → 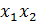. . . 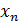граматики G, де 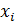∈ N ∪ T i замiнюємо вершину A ∈ N наступним деревом:

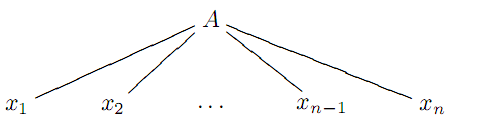Якщо конкатенацiя листкiв дерева виведення є словом ω ∈ 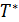,то кажемо, що дане дерево є деревом виведення для слова ω.

Дерево виведення слова ω вiдповiдає виведенню ω в граматицi G. Легко бачити, що часто дерево виведення вiдповiдає бiльш нiж одному виведенню слова ω. Контекстно вiльна граматика G = (N, T, S, P) називається не-однозначною, якщо iснує слово ω ∈ L(G), яке має два або бiльшерiзних дерев виведень.Розглянемо граматику G з правилами S → if b then S else S | if b then S | a.

Ця граматика неоднозначна, оскiльки слово

if b then if b then a else a

має два виводи

if b then (if b then a) else a та

if b then (if b then a else a),

яким вiдповiдають два рiзних дерева виведення.

4.Автомати Мілі та автомати Мура.Типи автоматів. Способи задання автоматів.

Розглянемо деякий пристрiй,який має n входiв i m виходiв. Будемо вважати, що на входи iнформацiя подається в дискретнi моменти часу 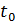, , 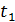. . . , 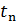. Iнтервалчасу 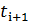− 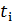називається тактом. Аналогiчно i з виходiв інформаціяодержується дискретно в часi. На кожному iз входiв (виходiв) сигналможе приймати дискретнi значення з деякого набору 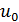, , 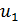. . . , 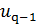.Сукупнiсть значень вхiдних сигналiв в момент часу 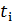називатимемо вхiдною буквою, а послiдовнiсть вхiдних букв – вхiдним словом.Множину всiх вхiдних букв назвемо вхiдним алфавiтом.Можна уявляти будь-який перетворювачiнформацiї як пристрiй з одним входом, на який надходять слова,складенi з букв вхiдного алфавiту, i з одним виходом, на якому одержуються слова в вихiдному алфавiтi.

Автоматом називають перетворювач алфавiтної iнформацiї, якиймає один вхiд i один вихiд. Для задання умов функцiонування автомата фiксуються три множини, елементами яких є букви трьох алфавтiв: вхiдного X = { 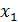, . . . , 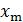}, вихiдного

Y = { 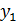, . . . , 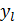} і множина внутрiшнiх станiв автомата Q = { , . . . , }.

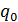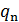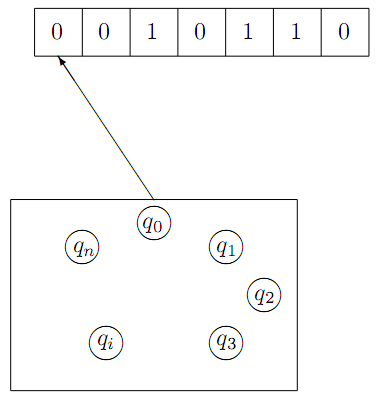Автомат складається з трьох частин – стрiчки, головки i керуючого пристрою. Стрiчка використовується для запису вхiдних даних (вхiдного слова). Вона подiлена на скiнченну кiлькiсть комiрок.

Головка переглядає стрiчку, читає букву з неї i передає одержану iнформацiю керуючому пристрою. Кожного разу головка переглядає тiльки одну комiрку стрiчки, читає записану в нiй букву i переходить до наступної комiрки праворуч. Керуючий пристрiй складається з станiв з множини станiв Q.

Семiрка A = (Q,X, Y, δ, f, 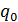, F) називається автоматом Мiлi, якщо вона складається iз множини станiв автомата Q, множини вхiдних символiв X, множини вихiдних символiв Y , функцiї переходiв δ : Q×X → Q, функцiї виходiв f : Q×X → Y , початкового стану 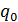та множини кiнцевих станiв F. Множини X i Y називають вiдповiдно вхiдним i вихiдним алфавiтами автомата. Якщо δ(a, x) = 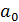, то кажуть, що автомат Q пiд дiєю вхiдного сигналу x ∈ X переходить в стан 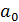, або сигнал x переводить автомат Q iз стану a в стан .

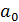Якщо, f(a, x) = y, то кажуть, що автомат Q перетворює в станi a вхiдний сигнал x ∈ X у вихiдний сигнал y ∈ Y .

Автомат A = (Q,X, Y, δ, f, 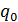, F) називається скiнченним, якщо всi три множини – Q, X i Y – скiнченнi, i нескiнченним, якщо хоч одна з них нескiнченна.

Автомат називається повним або повнiстю визначеним, якщо функцiї переходiв i виходiв повнiстю визначенi, i частковим, якщо хоч одна з них часткова.

Iнколи трапляються автомати, в яких компонент δ – не функцiя,а деяке вiдношення, тобто в таких автоматах не виконується умова однозначностi переходу. Автомати такого типу називаються недетермiнованими. Якщо ж вiдношення δ є функцiєю, то автомат називається детермiнованим. Отже, для детермiнованого автомата Q зпочатковим станом a однозначно знаходиться стан b, в який автоматперейде пiд дiєю слова ω ∈ F(X). А в недетермiнованому автоматi таких станiв може бути не один, а декiлька. Ясно, що клас детермiнованих автоматiв є пiдкласом класу недетермiнованих автоматiв.

Крiм класiв детермiнованих i недетермiнованих автоматiв, iснують i iншi спецiальнi класи. Серед них видiляються деякi виродженiкласи автоматiв, в яких одна з множин

(Q, X або Y ) одноелементна.

У таких випадках розглядаються спрощенi моделi автоматiв. Наведемо деякi приклади.

Автомат без пам’ятi - це трiйка (X, Y , f), де f : X → Y .

Цей автомат виконує посимвольну трансформацiю символiв вхідногоалфавiту X в символи вихiдного алфавiту Y , при якому на один ітой же вхiдний символ x ∈ X вiн реагує одним i тим же вихiдним символом y ∈ Y .

Автономний автомат – це четвiрка (Q, Y, δ, f) де δ : Q → Q, f : Q → Y . Для такого автомата поданням початкового стану визначається весь подальший процес його функцiонування.

Автомат без виходiв, або X-aвтомат – це п’ятiрка (Q,X, δ, 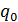, F), де F – деяка пiдмножина станiв автомата, елементи якої називаються кiнцевими або представляючими станами, а 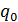∈ Q – початковий стан автомата.

Автомати Мура є окремим випадком автоматiв Мiлi. Автомат A = (Q,X, Y, δ, f) називається автоматом Мура, якщо його функція виходiв f(a, x) виражається функцiєю переходiв δ(a, x) за допомогою рiвняння f(a, x) = h(δ(a, x)), де h : Q → Y . В автоматi Мура вихiднийсигнал в момент часу t однозначно визначається станом автомата втой же момент часу, тобто y(t) = g(q(t)). Функцiя h називається функцiєю вiдмiток автомата, а її значення h(a) на станi a – вiдмiткою цього стану.

У загальному випадку для задання скiнченних автоматiв користуються двома стандартними способами, якi називаютьсяунiверсальними – це таблицi переходiв i виходiв та графи переходiв i виходiв.

Таблицi переходiв i виходiв автомата - це двi матрицi однакової розмiрностi, стовпчики яких вiдмiченi рiзними символами вхідного алфавiту, а рядки – рiзними символами станiв автомата. Для функцiї переходiв (перша матриця) на перетинi i-го рядка, вiдмiченого

вiдмiченого станом a ∈ Q i j-го стовпчика, вiдмiченого символом x ∈ X, знаходиться значення δ(a, x) = b. Аналогiчно для функції виходiв (друга матриця) – на перетинi i-го рядка i j-го стовпчика знаходиться значення f(a, x) = y ∈ Y . Вважають, що початковий

стан автомата вiдмiчає перший стовпчик як в таблицi переходiв, такi в таблицi виходiв.

Граф переходiв i виходiв скiнченного автомата A є альтернативним шляхом для зображення A. Вiн являє собою помiчений орiєнтований граф, вершини якого взаємно однозначно вiдповiдають станам автомата. Стрiлки графа вiдмiченi парами символiв: перший – символом вхiдного алфавiту, другий - символом вихiдною алфавiту. У цьому разi вiдповiднiсть мiж графом переходiв i виходiв i функцiями переходу δ i виходу f така, що коли δ(a, x) = 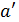i f(a, x) = y, то в графi з вершини 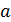у вершину 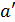веде стрiлка, вiдмiчена парою (x/y),i навпаки, коли в графi переходiв i виходiв автомата iснує стрiлка

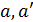( ), вiдмiчена парою (x/y), то для функцiй переходу δ i виходу f виконуються рiвностi δ(a, x) = 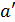i f(a, x) = y. Крiм того, щоб пiдкреслити початковий стан 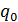, малюється стрiлка без початкової вершини, кiнцевою вершиною, якої є стан 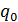. Кiнцевий стан позначається двома концентричними колами.

5. Детерміновані скінченні автомати без виходу.Алгоритми синтезу ДСА.

Якщо ж вiдношення δ є функцiєю, то автомат називається детермiнованим. Отже, для детермiнованого автомата Q зпочатковим станом a однозначно знаходиться стан b, в який автоматперейде пiд дiєю слова ω ∈ F(X).

Розглянемо рiзнi методи побудови детермiнованих скiнченних автоматiв (ДСА) без виходу.

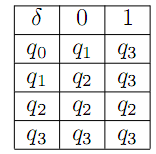
Пpиклад. Побудуємо граф ДСА A = (Q,X, δ, q₀, F) i знайдемо мову, яка розпiзнається A, якщо Q = {q0, q1, q2, q3}, X = {0, 1}, F ={q1, q2}, а функцiя переходiв δ задана таблицею:

Помiчений граф автомата A має вигляд:

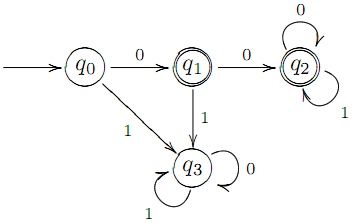
Знайдемо мову L(A), яка розпiзнається автоматом A.

Нагадаємо, що слово ω ∈ L(A), якщо автомат A зупиняє аналiз ω в одному з кiнцевих станiв множини F. З графа ДСА видно, що якщоавтомат переходить в стан q3 при аналiзi слова ω, то вiн залишається

в ньому до кiнця роботи i ω ∉ L(A). З другого боку, перейшовши в кiнцевий стан q₂, автомат нiколи не покине даного стану, i такiслова розпiзнаються ДСА. З вищесказаного випливає, що мова L(A) мiстить слово 0 (аналiз якого зупиняється в станi q1) i всi слова, якi мають префiкс 00. Таким чином, регулярний вираз мови L(A) маєвигляд 0 + 00(0 + 1 .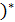

2.2. Пpиклад. Знайдемо мову, яка розпiзнається ДСА A = (Q,X, δ, q₀, F), заданого помiченим графом:

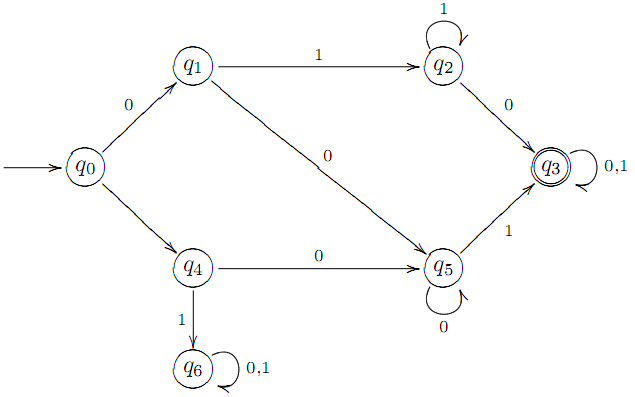Аналогiчно як у прикладi 3.2, якщо при аналiзi слова ω автомат переходить в стан q6, то дане слово не розпiзнається A i, навпаки, перейшовши в кiнцевий стан q₃, автомат розпiзнає слово ω. Отже, нам потрiбно проаналiзувати як зi стану q₀ можна перейти в стан q₃. Всього є три типи шляхiв з q₀ в q₃:

(q₀, q₁, q₂, . . . , q₂, q₃); (q₀, q₁, q₅, . . . , q₅, q₃); (q₀, q₄, q₅, . . . , q₅, q₃).

Вони вiдповiдають словам, префiкси яких належать регулярним мовам 01 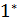0, 00 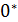1 i 10 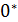1 вiдповiдно. Таким чином,

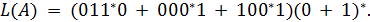
Пpиклад. Побудувати ДСА, який розпiзнає всi слова в бiнарному алфавiтi X = {0, 1}, якi мають префiкс 01.

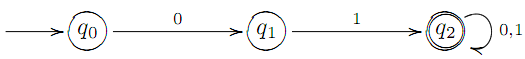Легко бачити, що регулярний вираз шуканої формальної мовимає вигляд 01(0 + 1 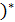. Побудуємо граф цього регулярного виразу:

Даний граф не є графом ДСА, оскiльки в графi ДСА з кожної вершини q має виходити єдина стрiлка з позначкою a для кожної пари (q, a) ∈ Q × X. Щоб виконати цю умову, побудуємо додаткову тупикову виршину q₃ i стрiлки q₀ → q₃ i q₁ → q₃ з позначками 1 i 0 вiдповiдно. Шуканий граф ДСА має вигляд:

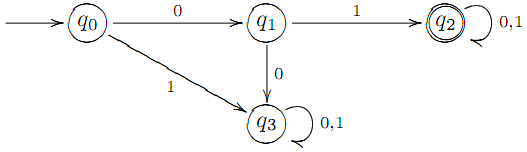Пpиклад. Побудувати ДСА, який розпiзнає всi слова в бiнарному алфавiтi X = {0, 1}, якi мiстять пiдслово 00.

Спершу вiдмiтимо, що з регулярного виразу (0+1 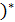00(0+1 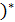неможна визначити перше входження пари 00 в вхiдному словi. З другого боку, шуканий ДСА мусить виявляти 00 вже при першому йоговходженнi у вхiдне слово. Проаналiзуємо дану проблему детальнiше.

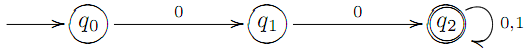Припустимо, що на стрiчцi записане слово ω = x₁x₂ . . . x_n, де x_i∈{0, 1}. Ми маємо перевiряти кожне пiдслово x₁x₂, x₂x₃, . . . x_n−1x_n i як тiльки виявиться, що якась пара рiвна 00, робити висновок, що слово w розпiзнається ДСА. Звiдси випливає наступний алгоритмпобудови ДСА.

Крок 1. Будуємо граф

з кiнцевою вершиною q₂, з допомогою якої розпiзнаються слова, що мiстять 00. Зокрема, якщо x₁x₂ = 00, то слово ω розпiзнається.

Крок 2. Якщо x₁ = 1, то ми залишаємо пiдслово x₁x₂ i переходимодо перевiрки x₂x₃. Таким чином, автомату потрiбно перейти в станq₀, тобто δ(q₀, 1) = q₀.

Крок 3. Якщо x₁ = 0 i x₂ = 1, то нi пiдслово x₁x₂, нi x₂x₃ недорiвнюють 00. Отже, керуючий пристрiй ДСА має перейти в стан q₀ для аналiзу пiдслова x₃x₄. Таким чином, покладаємо δ(q₁, 1) = q₀.Граф шуканого ДСА має вигляд:

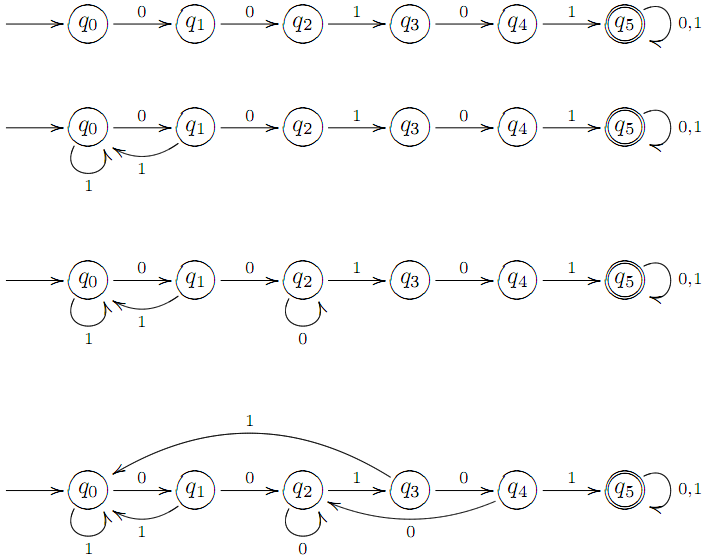
Пpиклад. Побудувати ДСА, який розпiзнає всi слова в бiнарному алфавiтi X = {0, 1}, якi мiстять пiдслово 00101.

Аналогiчно, як i в попередньому прикладi, крок за кроком будуємо шуканий ДСА:

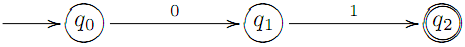Пpиклад. Побудувати ДСА, який розпiзнає всi слова в бiнарному алфавiтi X = {0, 1}, якi мають суфiкс 01. Спершу, побудуємо наступний граф:

Стани q₀ та q₁ вказують, що "не знайдено префiкса слова 01"та"знайдений префiкс 0 слова 01"вiдповiдно. Аналогiчно, як i в попередньому прикладi, покладемо

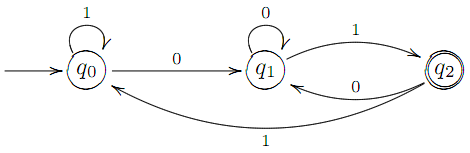δ(q₀, 1) = q₀ i δ(q₁, 0) = q₁. Якщоперейшовши в стан q₂ автомат не закiнчив аналiз вхiдного слова, тонеобхiдно покласти δ(q₂, 0) = q₁ i δ(q₂, 1) = q₀. Таким чином, шуканий граф ДСА має вигляд:

Теоpема. Клас формальних мов, якi розпiзнаються детермiнованими скiнченними автоматами, замкнений вiдносно скiнченних об’єднань, перетинiв, доповнення, рiзницi i симетричної рiзницi.

Iдея побудови ДСА для об’єднання цих мов, полягає в розглядi так званого добутку автоматiв. Нехай A₁ = (Q₁,X, δ₁, q₀, F₁) iA₂ = (Q₂,X, δ₂, q₀, F₂) – два автомати (вiдмiтимо, що Q₁ i Q₂ можуть мати стани з однаковими назвами, якi виконують рiзнi функції в двох ДСА). Визначимо добуток A = A₁ × A₂ автоматiв A₁ i A₂наступним чином. Нехай

A = (Q,X, δ, 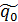, F). Покладемо

Q = Q₁ × Q₂ = {(q_i, q_j) | q_i∈ Q₁, q_j∈ Q₂},

δ((q_i, q_j), a) = (δ₁(q_i, a), δ₂(q_j , a)) i 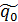= (q₀, q₀).

6. Недетерміновані скінченні автомати без виходу.Алгоритми синтезу НСА.

Iнколи трапляються автомати, в яких компонент δ – не функцiя,а деяке вiдношення, тобто в таких автоматах не виконується умова однозначностi переходу. Автомати такого типу називаються недетермiнованими.

Недетермiнований скiнченний автомат (НСА) без виходу (Q,X, δ, 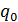, F)визначається так само як i ДСА за винятком того, що в ньому дозволяються переходи в декiлька станiв та e-переходи. Це означає, що для кожного стану q i вхiдної букви a значення δ(q, a) функції переходiв на парi (q, a) є пiдмножиною множини станiв Q, тобто

δ(q, a) = { 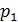, , 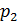. . . , 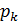}. Остання рiвнiсть означає, що проаналiзувавши букву a в станi q автомат може перейти в довiльний зi станів 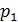, , 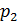. . . , або 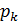. В випадку, коли δ(q, a) = ∅ автомат не переходит в жоден стан, "зависає"i вважаємо, що вхiдне слово не розпiзнається

НСА незважаючи на те, що деякi букви слова ще не проаналiзованi автоматом. Це рiвносильно тому, що ДСА перейшов в тупиковий стан. Крiм переходiв в декiлька станiв, в НСА дозволяються також e-переходи (e-такти). При e-переходi головка автомата нiчого не виконує (не читає i не рухається), але стан при цьому може змiнитися на довiльний зi станiв 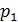, , 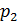. . . , або 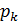. Таким чином, функцiя переходiв формально визначається як:

δ : Q × (X ∪ {e}) → 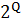,де через 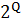позначається сiм’я всiх пiдмножин множини Q. Прикладом функцiї переходiв НСА 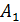є:

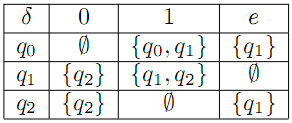НСА так як i ДСА задаються графами, вершинами яких є стани автомата, а за допомогою стрiлок зображаються переходи, тобто якщо

δ(q, a) = { 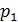, , 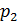. . . , 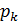}, то ми вiдкладаємо k стрiлок з вершини q до кожної з вершин 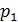, , 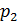. . . , 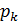i всi стрiлки помiченi буквою a.

Наприклад, граф розглянутого вище автомата A1 має вигляд (вважаємо, що F = { }):

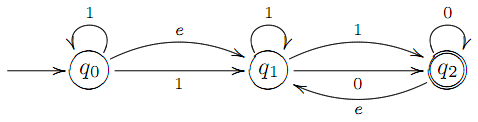На вхiдному словi ω НСА може мати бiльше нiж один обчислювальний шлях. В загальному випадку, обчислювальнi шляхи для вхiдного слова ω утворюють дерево виводу, оскiльки всi вони виходять з однiєї i тієї ж вершини 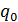i їх гiлки не утворюють циклiв.

Вважають, що автомат розпiзнає слово ω, якщо принаймi один з обчислювальних шляхiв закiнчується в кінцевому станi.

Щоб визначити строго, коли НСА розпiзнає вхiдне слово ω, потрiбно ввести поняття e-замикання. Назвемо e-замиканням пiдмножини P ⊂ Q множину станiв, якi досягаються з станiв q ∈ P e-переходами (включаючи переходи з q в q). Тобто,

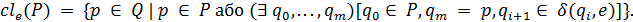
Продовжимо функцiю переходiв δ на множину 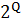× (X ∪ {e}),поклавши

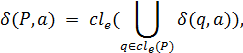
а далi продовжимо ї ї на 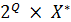наступним чином:

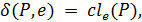
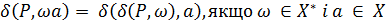
Тепер можна строго означити, що НСА (Q,X, δ, q₀, F) розпiзнає слово ω, якщо δ({q₀}, ω) ∩ F 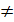∅. Через L(A) позначаємо мову, яка розпiзнається НСА A, тобто

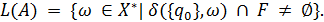
Теоpема. Клас формальних мов, якi розпiзнаються недетермiнованими скiнченними автоматами, замкнений вiдносно конкатинацiї та iтерацiї.

Хоча недетермiнованi скiнченнi автомати легше будуються нiждетермiнованi скiнченнi автомати, але, насправдi, вони є iдеалiзованими машинами i не можуть бути ефективно застосованi на практицi,оскiльки реальна машина може працювати тiльки єдиним обчислювальним шляхом в один i той же час. Виявляється, що для НСА єпроостий алгоритм для перетворення його в ДСА, який розпiзнає туж мову, що i НСА.

Розглянемо НСА A = (Q,X, δ, q₀, F). Для кожного ω∈ 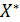позначимо через 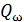множину станiв, якi є останнiми станами обчислювальних шляхiв слова ω, тобто 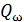= δ({q₀}, ω), де δ – функцiяпереходiв, визначена на множинi 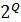× 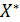. Зокрема, Q_e = cl_e({q₀}).

Таким чином, слово ω розпiзнається НСА тодii тiльки тодi, коли 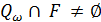. Отже, ми можемо взяти цi пiдмножини 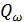⊂Q в якостi

станiв нового еквiвалентного ДСА. Iншими словами, побудуємо ДСА

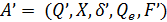з наступними компонентами:

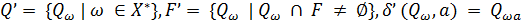, деω∈ 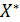, a∈X.

Вiдмiтимо, щокоженстан 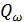єпiдмножиноюмножиниQi, отже, 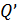єскiнченноюмножиною. Справдi, 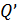⊂ 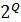i, отже, | | ≤ .

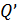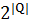Далi, якщ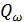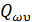о = , то 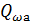= 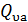длявсiхa∈X. Звiдсивипливає,щоозначенняфункцiїпереходiв 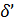єкоректним. Попереднiй аналiзпоказує, що конструкцiя ДСА є коректною. Дана конструкцiя називається побудовою ДСА за допомогою пiдмножин.

Теоpема 1. Формальна мова розпiзнається НСА тодii лише тодi, коли вона розпiзнається ДСА.

Теорема 1 дає нам простий метод побудови ДСА, який розпiзнає мову L: спершу ми будуємо НСА для L, а потiм перетворюємойого в еквiвалентний ДСА.

Твеpдження. Кожна регулярна мова розпiзнається деякимнедетермiнованим скiнченним автоматом.