Задачи минимизации с ограничениями равенствами

Мы рассмотрим условия экстремума и методы решения задач вида

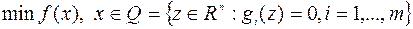(6.2.1)

где 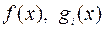– гладкие функции. Точки 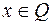называются допустимыми.

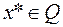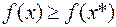
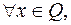
Условия минимума первого порядка (правило множителей Лагранжа). Точка называется локальной точкой минимума (или просто точкой минимума) в задаче (6.2.1), если 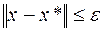при некотором .

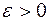Если 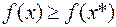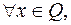то – то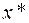чка глобального минимума.

Теорема 8 (необходимое условие минимума 1 порядка). Пусть 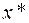– точка минимума в задаче (6.2.1), функции 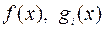непрерывно дифференцируемы в окрестности 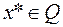. Тогда найдутся числа 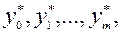не все равные 0, такие что

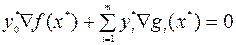. (6.2.2)

Будем называть 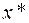регулярной точкой минимума, если функции 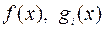непрерывно дифференцируемы в ее окрестности и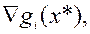 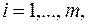линейно независимы.

Теорема 9 (правило множителей Лагранжа, необходимое условие минимума 1 порядка). Если 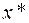– регулярная точка минимума в задаче (6.2.1), то найдутся числа 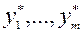такие, что

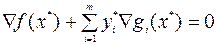. (6.2.3)

Доказательство теоремы 2 следует из теоремы 1, в силу линейной независимости векторов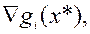

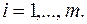
Числа 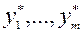в (6.2.3) называются множителями Лагранжа. Функция

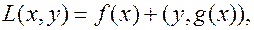
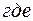
(6.2.4)

называется функцией Лагранжа (ФЛ). Правило множителей Лагранжа в терминах функции Лагранжа формулируется в виде:

(6.2.5)

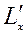где и 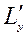– производные по соответствующим переменным. Здесь первое из условий (6.2.5) соответствует условию (6.2.3), а второе – это условия допустимост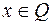и , или 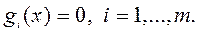Переменные 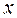называютпрямымипеременными, а 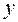– двойственными. Лишь при определенных условиях точка 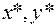является седловой точкой функции Лагранжа, т.е.

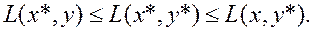(6.2.6)

Условия минимума второго порядка.

Теорема 10 (необходимое условие II порядка). Пусть 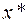– регулярная точка минимума в задаче (6.2.1), функции 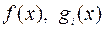дважды непрерывно дифференцируемы в окрестности 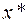, а 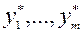– множители Лагранжа. Тогда

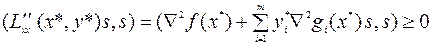(6.2.7)

для всех .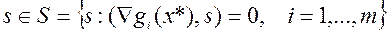

Можно сказать, матрица вторых производных функции Лагранжа в точке минимума 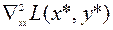неотрицательно определена на касательном подпространстве 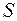, т.е. на подпространстве, смещения в котором не контролируются ограничениями. Поэтому вдоль этих направлений применяются условия безусловной минимизации.

Достаточные условия минимума для некоторой точки позволяют утверждать, что она является точкой минимума.

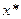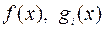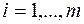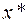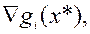
Теорема 11 (достаточное условие II порядка).Пусть – допустимая точка, функции , , дважды дифференцируемы в окрестности , 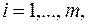линейно независимы, выполнено необходимое условие минимума (6.2.5) и

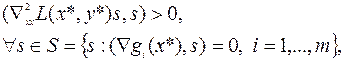(6.2.8)

Тогда 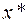– точка локального минимума в задаче (6.2.1).

Таким образом, матрица вторых производных функции Лагранжа в точке минимума 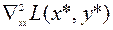строго положительно определена на касательном подпространстве 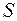, т.е. на подпространстве, смещения в котором не контролируются ограничениями. Поэтому вдоль этих направлений применяются условия безусловной минимизации.

Точку 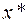, в которой выполняются условия теоремы 4, будем называть невырожденной точкой минимума (невырожденным минимумом).

Введем модифицированную функцию Лагранжа

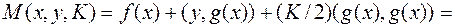
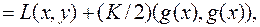(6.2.9)

где 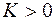– некоторый параметр. Необходимые условия экстремума (6.2.5) можно записать, используя функцию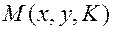

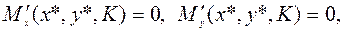(6.2.10)

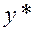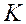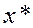где множители Лагранжа те же, что и в (6.2.5). Оказывается, при достаточно больших точка является точкой минимума функции 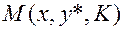при условиях теоремы 4. Для обычной функции Лагранжа последнее свойство не всегда выполняется, хотя точка 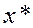является стационарной точкой.

Пример 1. Найти экстремумы функции 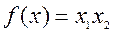, при ограничении .

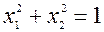Составим функцию Лагранжа

.

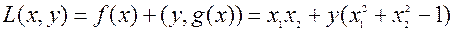Первое из условий (6.2.5) 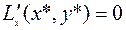дает систему

.

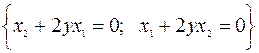Отсюда найдем 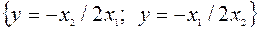. Отсюда следует взаимосвязь 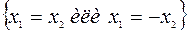. Используя полученные соотношения в ограничении, получим возможные решения для подозрительных точек 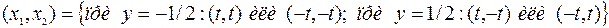, где .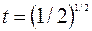

Исследуем матрицу вторых производных при различных значениях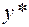

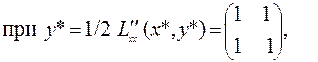
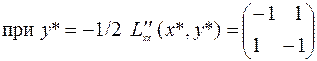(6.2.11)

При 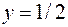направление 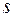, ортогональное градиентам в точках 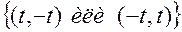будет 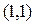. Согласно (6.2.11) для этого 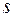будет выполнено (6.2.8). Поэтому точки 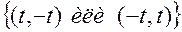будут точками минимума. При 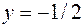для точек 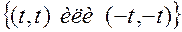получается , что соответствует условию максимума функции. Для проверки этого следует сменить знак функции и решить задачу заново. В результате для точек 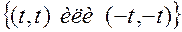будет выполнено условие минимума, что означает максимум исходной функции.

Пример 2. Решить задачу

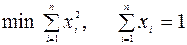. (6.2.12)

Составим функцию Лагранжа

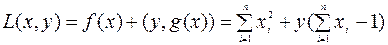(6.2.13)

Условие стационарности

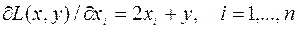. (6.2.14)

Отсюда и условия допустимости следует 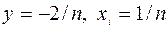. Поскольку матрица вторых производных функции Лагранжа положительно определена для всех 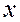, то 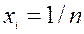является точкой минимума.