Уравнения параболического типа

1. Начальные и граничные условия.

Для тела линейного размера, например, для стержня, температура 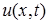в точке 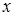в момент времени 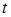удовлетворяет уравнению теплопроводности:

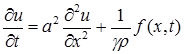(1)

Здесь ,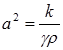

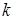– коэффициент внутренней теплопроводности,

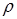– плотность вещества,

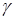– теплоёмкость вещества,

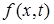– мощность внутренних источников тепла в стержне, рассчитанная на единицу массы.

Для однородного стержня 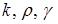постоянны.

Для выделения единственного решения уравнения теплопроводности необходимо к уравнению присоединить начальные и краевые условия.

Начальное условие (в отличие от уравнения гиперболического типа) состоит лишь в задании значений функции 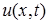в некоторый начальный момент времени, например, при . Иначе, в начальный момент времени распределение температуры вдоль стержня считается известным

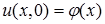(2)

Для стержня конечных размеров 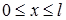задаются условия на его концах –граничные, или краевые условия, которые могут быть различны в зависимости от температурного режима на концах.

Рассматриваются три типа граничных условий.

Краевые условия первого типа. На концах стержня поддерживается заданная температура (задан тепловой режим) – условия налагаются на функцию :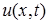

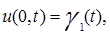
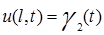(3)

В частности, эти условия могут быть однородными (на концах стержня все время поддерживается нулевая температура:

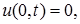
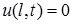
Краевые условия второго типа. На концах стержня заданы тепловые потоки 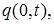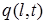, проходящие через торцевые сечения стержня и направленные из тела во внешнюю среду. Так как поток пропорционален нормальной производной 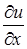, то можно задать

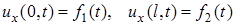(4)

Условия налагаются на производную .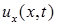

В частном случае, когда концы стержня теплоизолированы (тепловой поток отсутствует), граничные условия (4) становятся однородными:

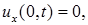
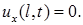
Краевые условия третьего типа. На концах стержня происходит теплообмен со средой по закону Ньютона.

Закон Ньютона.Величина теплового потока через границу тела пропорциональна разности температур тела на границе и внешней среды:

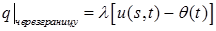
где 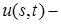температура тела на границе, 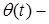температура среды.

В частности, для стержня граничные условия можно записать так:

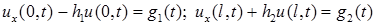(5)

На концах задано линейное соотношение между функцией 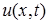и производной 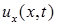. Здесь 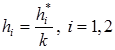, 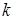– коэффициент теплопроводности стержня, 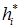– коэффициент теплообмена на правом ( 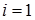) и левом ( 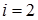) торце стержня.

Смешанные задачи.На разных концах стержня задаются условия различных типов.