Глава 2. элементы векторной алгебры
§ 1. ВЕКТОР. АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ С
ВЕКТОРАМИ.
Различают понятия величин, которые характеризуются од -ним числом - скалярные величины (например: масса, объём, длина, площадь и т.д.) и величин, для которых имеет значе -ние не только их численное значение, но и направление их действия - векторных величин (например: сила, скорость, ус - корение и т.д.).
Вектором называется направленный отрезок 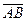 , где
, где 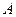 - начало вектора,
- начало вектора, 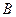 - конец вектора.
- конец вектора.
В физике важное значение имеет точка приложения вектора, т.е. начальная точка 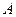 . Векторы в математике чаще всего не связывают с точкой приложения, поэтому часто геометрический вектор обозначается
. Векторы в математике чаще всего не связывают с точкой приложения, поэтому часто геометрический вектор обозначается 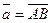 . Чтобы объяснить это, введём сначала несколько понятий. Длина вектора обозначается
. Чтобы объяснить это, введём сначала несколько понятий. Длина вектора обозначается 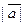 или
или 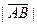 . Вектор, начало и конец которого совпадают, называется нулевым. Его длина равна нулю. Считается, что его направление совпадает с направлением любого вектора, и он обозначается
. Вектор, начало и конец которого совпадают, называется нулевым. Его длина равна нулю. Считается, что его направление совпадает с направлением любого вектора, и он обозначается 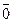 .
.
Векторы, лежащие на одной прямой, или на параллельных прямых, называются коллинеарными.
Векторы, лежащие в одной плоскости, или в параллельных плоскостях, называются компланарными.
Векторы называются равными, если они коллинеарны, име- ют одинаковую длину и одинаково направлены.
Из этого определения следует, что векторы равны, если их можно совместить с помощью параллельного переноса. Равен-ство векторов не зависит от их начальных точек (точек прило- жения); таким образом, начальную точку любого вектора с помощью параллельного переноса можно совместить с любой точкой плоскости или пространства. В этом смысле геометри- ческие векторы называются свободными.
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ


 1. Сложение векторов. Суммой двух векторов
1. Сложение векторов. Суммой двух векторов 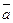 и
и  называется вектор
называется вектор 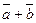 , идущий из начала вектора
, идущий из начала вектора 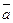 в конец вектора
в конец вектора  .
.
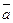

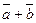
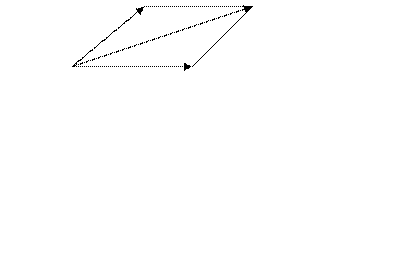
Это определение называется правилом треугольника сложе - ния векторов. Другое определение суммы векторов называется правилом параллелограмма: вектор суммы векторов направлен по диагонали параллелограмма, построенного на векторах 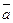 и
и  , т.е
, т.е
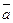
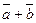

2. Умножение вектора на число. При умножении вектора 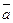 на число
на число 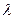 получаем вектор
получаем вектор 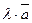 , коллинеарный данному вектору, длина которого изменяется в
, коллинеарный данному вектору, длина которого изменяется в 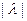 раз, причём на- правление вектора сохраняется, если
раз, причём на- правление вектора сохраняется, если 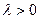 и меняется на противоположное, если
и меняется на противоположное, если 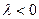 .
.
Из сказанного выше следует ещё одно определение кол – линеарности векторов.
ОПРЕДЕЛЕНИЕ 1. Вектора 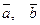 называются коллинеар- ными, если существует некоторое действительное число
называются коллинеар- ными, если существует некоторое действительное число 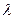 , такое, что
, такое, что 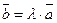 .
.
Операции сложения и умножения вектора на число обладают следующими свойствами:
1.  (коммутативность сложения);
(коммутативность сложения);
2. 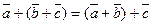 (ассоциативность сложения);
(ассоциативность сложения);
3. 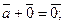
4. 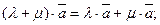
5. 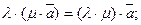
6. 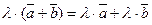 .
.
7. 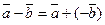 .
.
Вычитание векторов на картинке выглядит следующим обра- зом:



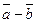

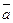
Вектор разности направлен в сторону вектора, из которого вычитается второй вектор.
Дальнейшее изучение векторов связано с понятием систе- мы координат
§ 2 СИСТЕМЫ КООРДИНАТ НА ПРЯМОЙ, НА ПЛОСКОС-
ТИ И В ПРОСТРАНСТВЕ.
1. Координата на прямой вводится следующим образом: на прямой стрелкой указывается направление положительного изменения, определяется начало отсчёта - точка О и опре –деляется масштабная единица




 1
1



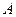
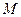
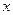
Координатой произвольной точки 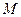 называют длину отрезка
называют длину отрезка 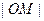 , вычисленную в масштабных единицах ( в данном случае, координата точки
, вычисленную в масштабных единицах ( в данном случае, координата точки 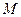 равна
равна 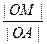 ), причём, если точка
), причём, если точка 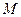 находится правее точки
находится правее точки 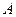 , то знак координаты по- ложительный, а если левее, то отрицательный. Если даны две точки на прямой
, то знак координаты по- ложительный, а если левее, то отрицательный. Если даны две точки на прямой 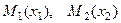 , то расстояние между ни -ми ищется по формуле:
, то расстояние между ни -ми ищется по формуле:
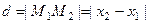 . (1)
. (1)
2. Декартова (прямоугольная) система координат на пло-скости задаётся двумя взаимно перпендикулярными осями. Точка их пересечения  - это начало координат, на каждой оси вводится масштабная единица.
- это начало координат, на каждой оси вводится масштабная единица.
 |
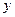


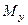
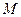

 1
1

 О 1
О 1 
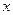
Ось 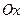 называется осью абсцисс, ось
называется осью абсцисс, ось  - осью ординат.
- осью ординат.
Координатами произвольной точки 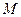 в данной системе ко- ординат называются числа
в данной системе ко- ординат называются числа 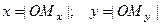 , вычис -ленные в масштабных единицах, причём эти координаты будут положительными, если точка
, вычис -ленные в масштабных единицах, причём эти координаты будут положительными, если точка 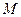 расположена правее (выше) соответствующей координатной оси. В данной системе коор –динат:
расположена правее (выше) соответствующей координатной оси. В данной системе коор –динат: 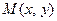 .
.
Расстояние между двумя точками 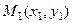 и
и  на плоскости вычисляется по формуле:
на плоскости вычисляется по формуле:
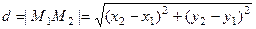 . (2)
. (2)
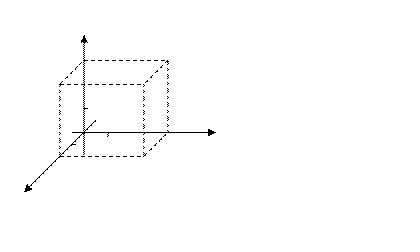 3. В пространстве декартова (прямоугольная) система ко -ординат определяется осями, которые лежат в пересечениях трёх взаимно перпендикулярных плоскостей, пересекающихся в одной точке. Сами эти плоскости называются координатными плоскостями
3. В пространстве декартова (прямоугольная) система ко -ординат определяется осями, которые лежат в пересечениях трёх взаимно перпендикулярных плоскостей, пересекающихся в одной точке. Сами эти плоскости называются координатными плоскостями 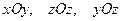 , соответственно. На каждой оси вводится масштабная единица
, соответственно. На каждой оси вводится масштабная единица
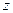
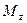
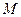
 1
1 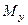
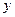

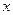
Ось 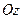 называется осью аппликат. Точка в пространстве имеет три координаты
называется осью аппликат. Точка в пространстве имеет три координаты  . Расстояние между двумя точками
. Расстояние между двумя точками 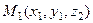 и
и 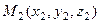 в пространстве опре- деляется по формуле, которая аналогична соответствующей формуле для плоскости:
в пространстве опре- деляется по формуле, которая аналогична соответствующей формуле для плоскости:
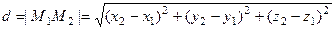 (3)
(3)
4. Чтобы установить связь между векторами и системой ко-
ординат, требуется ввести понятие проекции вектора на ось.
Пусть дана произвольная ось 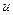 и некоторый вектор
и некоторый вектор 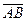 :
:
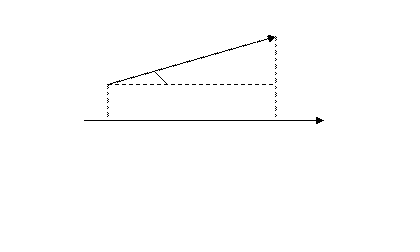
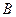
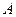
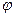
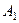
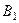
Величина направленного отрезка с соответствующим знаком 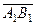 оси
оси 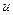 называется проекцией вектора
называется проекцией вектора 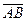 на ось
на ось 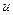 и обозначается
и обозначается  . Из рисунка видно, что:
. Из рисунка видно, что:
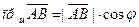 .
.
Если угол 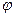 острый, то проекция положительна, если тупой, то проекция отрицательна. Проекции равных векторов на одну и ту же ось равны.
острый, то проекция положительна, если тупой, то проекция отрицательна. Проекции равных векторов на одну и ту же ось равны.
Проекции векторов имеют два основных свойства:
1. Проекция суммы векторов равна сумме их проекций. 
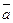

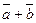
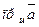

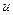
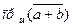
Из рисунка видим, что
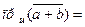

 .
.
2. При умножении вектора на число его проекция умно -
жается на то же число:
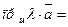
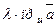 .
.
Рассмотрим произвольный вектор 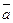 и его проекции на оси координат. Вектор однозначно определяется своими проекция -ми на оси координат. (Равные векторы можно совместить параллельным переносом и они имеют одинаковые проекции, и наоборот, векторы с одинаковыми проекциями равны.)
и его проекции на оси координат. Вектор однозначно определяется своими проекция -ми на оси координат. (Равные векторы можно совместить параллельным переносом и они имеют одинаковые проекции, и наоборот, векторы с одинаковыми проекциями равны.)
Считаем, что вектор 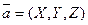 имеет проекции на оси координат равные, соответственно,
имеет проекции на оси координат равные, соответственно, 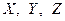 . Причём, если вектор
. Причём, если вектор 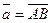 , где
, где 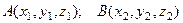 , то координа- ты вектора
, то координа- ты вектора 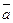 равны, соответственно,
равны, соответственно,

Таким образом, чтобы найти координаты вектора 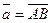 (т.е. его проекции на оси координат) необходимо из координат
(т.е. его проекции на оси координат) необходимо из координат 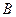 - конечной точки вектора вычесть соответствующие коорди- наты точки
- конечной точки вектора вычесть соответствующие коорди- наты точки 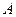 - начальной точки вектора.
- начальной точки вектора.
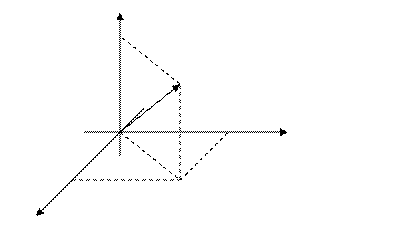
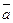

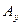
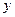
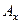
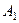
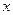
Вектор 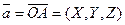 называется радиус – вектором точки
называется радиус – вектором точки 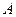 . Из треугольника
. Из треугольника 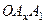 :
:
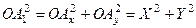 .
.
Тогда из треугольника  имеем:
имеем:
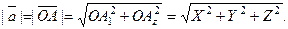
В частности, для вектора 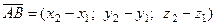 получаем:
получаем: 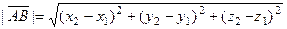 , т.е. длина вектора
, т.е. длина вектора 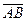 равна расстоянию между точками A и В.
равна расстоянию между точками A и В.
Если 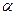 - угол между вектором
- угол между вектором 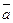 и осью
и осью 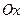 ,
, 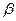 - угол между вектором
- угол между вектором 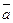 и осью
и осью  и
и 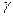 - угол между вектором
- угол между вектором 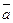 и осью
и осью 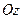 , то
, то 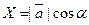 ,
, 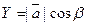 ,
, 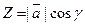 , то получаем понятия, так называемых направляющих косинусов вектора :
, то получаем понятия, так называемых направляющих косинусов вектора :
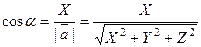 ;
; 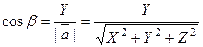 ;
;
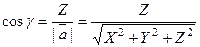 .
.
Основное свойство направляющих косинусов, которое легко проверяется непосредственно:
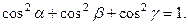 (!)
(!)
Рассмотрим пример: найти вектор 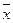 , длина которого
, длина которого 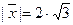 , который образует равные острые углы с осями координат.
, который образует равные острые углы с осями координат.
По условию: 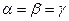 , поэтому, по свойству (!),
, поэтому, по свойству (!),
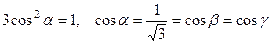 . (знак «+», так как углы острые), тогда
. (знак «+», так как углы острые), тогда  .
.
Таким образом, вектор 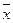 имеет координаты:
имеет координаты: 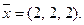
Рассмотрим задачу о делении отрезка в данном отноше -нии. Пусть даны две точки 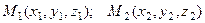 . Требуется найти координаты точки
. Требуется найти координаты точки 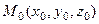 , которая делит отрезок
, которая делит отрезок 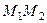 в отношении
в отношении 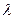 , т.е отношение длин отрезков
, т.е отношение длин отрезков
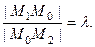
Рассмотрим случай проекций на ось 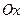 . ( Для остальных осей формулы получаются аналогичным образом).
. ( Для остальных осей формулы получаются аналогичным образом).
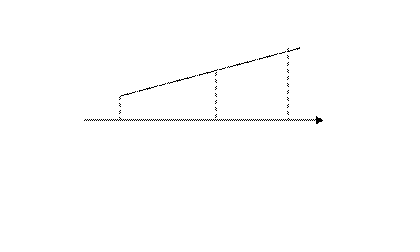
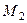
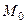

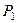


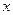
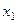
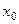
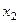
Так как параллельные прямые отсекают на сторонах угла пропорциональные отрезки, то
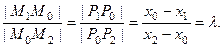
Тогда 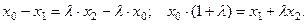 Таким образом,
Таким образом,

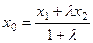 , аналогично,
, аналогично, 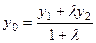 ;
; 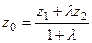 .
.
В частности, если 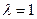 , т.е. отрезок делится пополам, получаем координаты середины отрезка:
, т.е. отрезок делится пополам, получаем координаты середины отрезка:
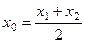 ;
;  ;
; 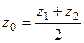 . (+) Таким образом, координаты середины отрезка равны полу -сумме координат концов отрезка.
. (+) Таким образом, координаты середины отрезка равны полу -сумме координат концов отрезка.
Пример. Найти координаты центра масс треугольника с 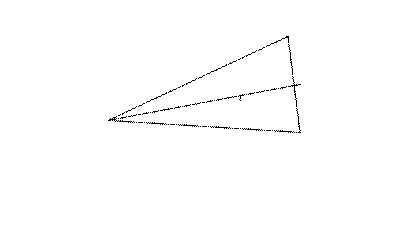 вершинами:
вершинами: 
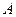
О 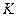
Центр масс треугольника всегда находится в точке пересече -ния медиан, а медиана треугольника делит сторону пополам, тогда, по формулам (+), точка 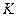 имеет координаты
имеет координаты
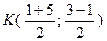 , или
, или 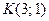 .
.
Другое свойство медиан треугольника: медианы в точке пере- сечения делятся в отношении 2 : 1, считая от вершины треу –гольника, поэтому точка 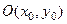 - центр масс (точка пере -сечения медиан) делит отрезок
- центр масс (точка пере -сечения медиан) делит отрезок  в отношении:
в отношении:
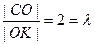 .
.
Тогда 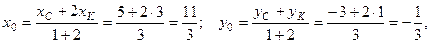
Таким образом 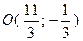 .
.
Вернёмся снова к линейным операциям над векторами.
Пусть даны два вектора  . Тогда, учитывая свойства проекции вектора на ось, получаем следующие правила:
. Тогда, учитывая свойства проекции вектора на ось, получаем следующие правила:
1) 
2) 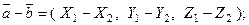
3) 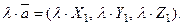
Из последней формулы, учитывая определение коллинеарнос- ти векторов, получаем следующее условие коллинеарности:
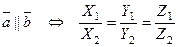 .
.
Рассмотрим пример: пусть даны два вектора
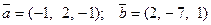 .
.
Проверить коллинеарность векторов  .
.
Найдём координаты векторов:
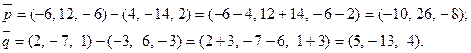 Проверим выполнение условия коллинеарности:
Проверим выполнение условия коллинеарности:

Координаты векторов пропорциональны, следовательно векторы коллинеарны, т.е. 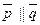 .
.
В заключение, придадим другой смысл проекциям вектора на координатные оси. С этой целью в заданной системе координат определим тройку векторов 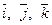 следующим образом:
следующим образом:
1) векторы 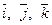 лежат на осях
лежат на осях 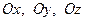 , соответст- вено, т.е. взаимно перпендикулярны. Их направления совпада- ют с положительными направлениями соответствующих коор -динатных осей;
, соответст- вено, т.е. взаимно перпендикулярны. Их направления совпада- ют с положительными направлениями соответствующих коор -динатных осей;
2) 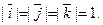
Единичные взаимно перпендикулярные векторы по другому называются ортами. В системе координат 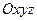 эти векторы имеют следующие координаты:
эти векторы имеют следующие координаты:
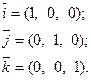
Тогда любой вектор 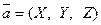 можно записать следу- ющим образом:
можно записать следу- ющим образом: 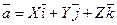 , т.е. любой вектор прост –ранства можно представить в виде линейной комбинации век- торов
, т.е. любой вектор прост –ранства можно представить в виде линейной комбинации век- торов 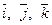 . Таким образом, векторы
. Таким образом, векторы 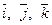 представляет собой естественный базис прямоугольной системы координат в пространстве.
представляет собой естественный базис прямоугольной системы координат в пространстве.
ЗАМЕЧАНИЕ. Любые три некомпланарных вектора прост –ранства образуют его базис , т.е. любой другой вектор прост- ранства можно представить в виде линейной комбинации этих векторов.
§ 3. НЕЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ.
Нелинейными операциями являются операции умножения векторов.
1. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
Скалярным произведением векторов 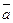 и
и  называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.
называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.
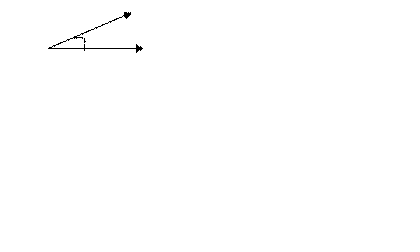
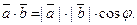 (1)
(1)
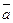
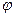

Так как 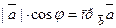 ,
, 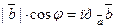 , то получаем:
, то получаем:
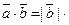
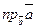 =
= 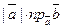 (2)
(2)
Отсюда получаем формулы для вычисления проекций:
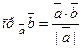 ;
; 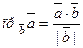 . (3)
. (3)
Также, учитывая формулу (1),
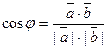 . (4)
. (4)
Скалярное произведение векторов имеет простой механи – ческий смысл : Скалярное произведение 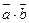 равно работе силы
равно работе силы 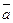 по перемещению материальной точки из начала в конец вектора
по перемещению материальной точки из начала в конец вектора  .
.
Легко доказать следующие свойства скалярного произ –ведения:
1. 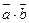 =
=  (коммутативность);
(коммутативность);
2. 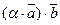 =
= 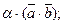
3. 
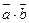
 (дистрибутивность);
(дистрибутивность);
4. 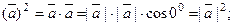 тогда
тогда 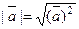 ;
;
5. Условие ортогональности векторов:
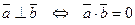 ,
,
так как 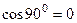 .
.
Эти свойства позволяют выполнить следующие задания:
1). Пусть 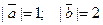 ; угол между этими векторами
; угол между этими векторами 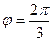 . Найти длину вектора
. Найти длину вектора 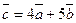 .
.
По свойству 4,
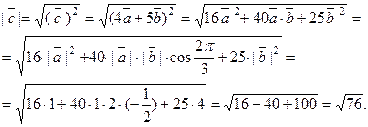
2). Пусть  ; угол между этими векторами
; угол между этими векторами 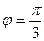 . Найти
. Найти 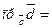
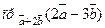 .
.
По формуле (3),  . В данных условиях,
. В данных условиях,
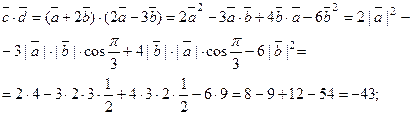
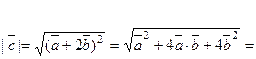
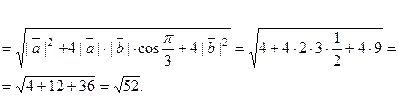
Тогда 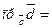
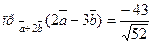 .
.
Пусть теперь векторы заданы своими координатами:
 в базисе
в базисе 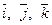 . При вы- числении скалярного произведения базисных векторов получим:
. При вы- числении скалярного произведения базисных векторов получим: 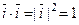 , по свойству 4. Аналогично
, по свойству 4. Аналогично 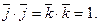 Так как векторы
Так как векторы 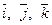 ортогональны, т.е. попарно перпендику –лярны, то, по свойству 5,
ортогональны, т.е. попарно перпендику –лярны, то, по свойству 5, 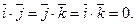 Тогда
Тогда 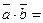
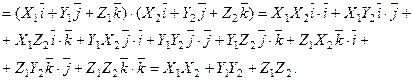
Таким образом, скалярное произведение векторов, заданных координатами, равно сумме произведений соответствующих координат:
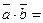
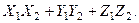 (5)
(5)
Тогда векторы ортогональны если
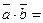

Угол между векторами 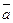 и
и  можно найти по формуле:
можно найти по формуле:
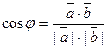 =
= 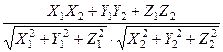 . (6)
. (6)
Рассмотрим ещё несколько примеров:
1. Даны векторы 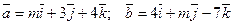 . При
. При
каком значении 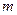 эти векторы перпендикулярны ?
эти векторы перпендикулярны ?
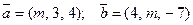 .
.  , так как векторы перпендикулярны. Тогда
, так как векторы перпендикулярны. Тогда 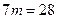 или
или 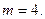
2. Треугольник задан своими вершинами: А(2, -1, 3),
В(1, 1, 1), С(0, 0, 5). Найти углы треугольника АВС.
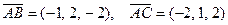 , тогда по формуле (6),
, тогда по формуле (6),
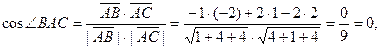
Следовательно  .
.
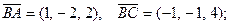 тогда по той же формуле,
тогда по той же формуле,

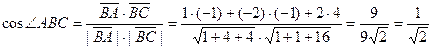 и угол
и угол 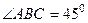 . Тогда
. Тогда 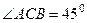 .
.
3. Проверить, что четырёхугольник с вершинами:  является квадратом.
является квадратом.
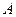
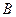
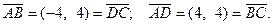
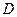
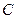
Следовательно, противоположные стороны параллельны и оп- ределяются одинаковыми векторами. Тогда данный четы- рёхугольник является параллелограммом. Найдём длины смеж- ных сторон: 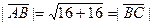 . Т.е. все стороны равны. Параллелограмм с равными сторонами является ромбом. Чтобы доказать, что ромб является квадратом, достаточно доказать перпендикулярность хотя бы двух смежных сторон. Найдём скалярное произведение:
. Т.е. все стороны равны. Параллелограмм с равными сторонами является ромбом. Чтобы доказать, что ромб является квадратом, достаточно доказать перпендикулярность хотя бы двух смежных сторон. Найдём скалярное произведение:
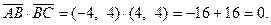
Выполнено условие ортогональности векторов 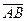 и
и 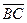 , сле- довательно
, сле- довательно 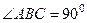 , и тогда рассматриваемый четы- рёхугольник является квадратом.
, и тогда рассматриваемый четы- рёхугольник является квадратом.
2. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
Векторным произведением вектора 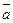 на вектор
на вектор 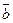 называ- ется вектор, обозначаемый
называ- ется вектор, обозначаемый 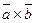 , или
, или 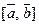 , который опреде- ляется тремя условиями:
, который опреде- ляется тремя условиями:
1) Вектор  перпендикулярен векторам
перпендикулярен векторам 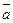 и
и 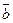 , т.е.
, т.е. 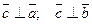 :
:
2) Длина вектора - 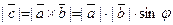 :
:
3) Векторы 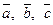 образуют «правую тройку».
образуют «правую тройку». 
 Векторы
Векторы 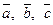 образуют правую
образуют правую
тройку, если они имеют общее на-
чало и из конца вектора 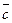 крат -
крат -
чайший поворот вектора 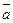 к век –
к век –
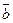 тору
тору 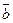 виден против часовой
виден против часовой
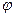 стрелки.
стрелки.
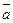
Механический смысл векторного произведения: вектор- ное произведение 
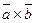 равно моменту силы
равно моменту силы 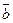 , при -ложенной к концу вектора
, при -ложенной к концу вектора 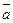 относительно начала век -тора
относительно начала век -тора 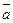 .
.
Свойства векторного произведения.
1. 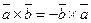 ;
;
Если поменяем местами векторы 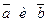 , то тройка
, то тройка
векторов 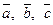 поменяет ориентацию (станет левой)
поменяет ориентацию (станет левой)
и вектор 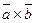 сменит направление на противополож-
сменит направление на противополож-
ное.
2. Если векторы 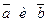 имеют одно и то же начало, то
имеют одно и то же начало, то
модуль (длина) векторного произведения численно ра –
вен площади параллелограмма, построенного на век –
торах  (произведение длин сторон на синус угла
(произведение длин сторон на синус угла
между ними). Таким образом: 
площадь параллелограмма 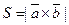 , а
, а
площадь треугольника 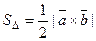
3. Если векторы 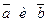 коллинеарны, то их векторное произведение равно 0, т.е.
коллинеарны, то их векторное произведение равно 0, т.е. 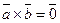 . Это ещё одно ус- ловие коллинеарности векторов. (если векторы колли –неарны, т.е. параллельны, то
. Это ещё одно ус- ловие коллинеарности векторов. (если векторы колли –неарны, т.е. параллельны, то 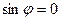 и, по условию 1) определения, вектор имеет нулевую длину).
и, по условию 1) определения, вектор имеет нулевую длину).
В частности, 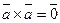 для любого вектора.
для любого вектора.
4.  (Постоянный множитель можно выносить за скобку).
(Постоянный множитель можно выносить за скобку).
5. 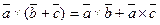 . (Можно раскрывать скобки.)
. (Можно раскрывать скобки.)
Рассмотрим пример: найти площадь параллелограмма, по -строенного на векторах 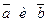 , которые заданы следующим образом:
, которые заданы следующим образом: 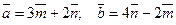 , если
, если 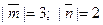 и угол между векторами
и угол между векторами 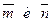 равен
равен 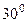 .
.
По свойству 2, 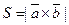 . Найдём:
. Найдём:
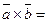

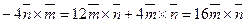 . Тогда
. Тогда
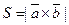
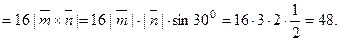
При решении примера мы использовали свойства вектор- ного произведения. По свойству 3, 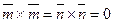 , по свой- ству 1,
, по свой- ству 1, 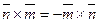 .
.
Пусть теперь векторы заданы своими координатами:
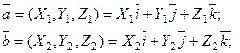 (7)
(7)
где базисные векторы 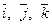 имеют единичную длину, вза -имно перпендикулярны и образуют правую тройку. Тогда для них выполняются следующие правила векторного умножения :
имеют единичную длину, вза -имно перпендикулярны и образуют правую тройку. Тогда для них выполняются следующие правила векторного умножения :

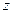
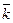
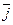
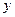
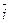 О
О
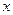
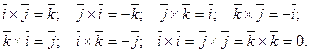
Найдём векторное произведение векторов 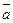 и
и 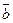 , используя эти правила, умножив векторы, заданные формулой (7), как скобку на скобку.
, используя эти правила, умножив векторы, заданные формулой (7), как скобку на скобку.
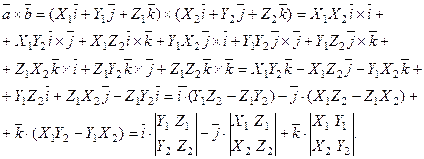
Но последнее выражение задаёт разложение по первой строке следующего определителя, т.е.
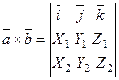 . (8)
. (8)
Пример. Найти площадь треугольника с вершинами 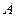 (1, 1, 1),
(1, 1, 1),
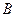 (2, 3, 4) и
(2, 3, 4) и 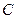 (4, 3, 2) и его высоту, опущенную из вершины
(4, 3, 2) и его высоту, опущенную из вершины 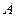 .
.

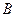
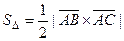
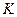
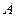
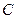
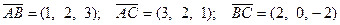 .
.
Найдём векторное произведение:
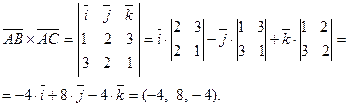
Тогда

Высоту треугольника можем найти следующим образом:

3. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
Для трёх векторов можно ввести смешанное произведение, при котором два вектора перемножаются векторно и получен- ный в результате вектор скалярно умножается на третий век- тор, в результате чего получается число.
Смешанное произведение векторов обозначается:
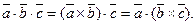
Любая циклическая перестановка не меняет смешанное произ- ведение: 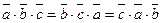 . Остальные перестановки меняют знак произведения на противоположный.
. Остальные перестановки меняют знак произведения на противоположный.
ТЕОРЕМА. Смешанное произведение векторов равно
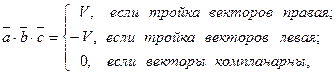
где 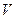 - объём параллелепипеда, построенного на векторах
- объём параллелепипеда, построенного на векторах 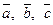 .
.
В самом деле, рассмотрим рисунок

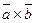
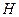
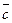
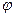
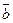
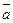
Тогда , если учесть, что 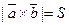 - площадь параллело- грамма, построенного на векторах
- площадь параллело- грамма, построенного на векторах 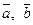 , а
, а 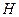 - высота, построенного параллелепипеда, то
- высота, построенного параллелепипеда, то
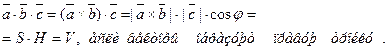
Если векторы образуют левую тройку, то вектор 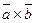 направлен в противоположную сторону, угол
направлен в противоположную сторону, угол 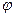 тупой и
тупой и 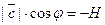 , и
, и 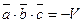 . Если векторы компла -нарны, то
. Если векторы компла -нарны, то 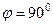 и смешанное произведение равно 0.
и смешанное произведение равно 0.
Условие компланарности векторов:
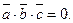 (9)
(9)
Если векторы не компланарны, т.е. 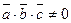 , то они образуют базис, т.е. любой вектор пространства можно представить в виде их линейной комбинации.
, то они образуют базис, т.е. любой вектор пространства можно представить в виде их линейной комбинации.
Если векторы заданы своими координатами:  , то, как в случае скалярного и векторного произведения, можно показать, что:
, то, как в случае скалярного и векторного произведения, можно показать, что:
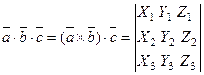 . (10)
. (10)
Учитывая теорему, можно найти объём параллелепипеда, построенного на векторах 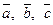 , по формуле:
, по формуле:

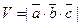 ,
,
а объём треугольной пирамиды, построенной на тех же векторах:
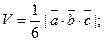 (11)
(11)
высоту параллелепипеда или пирамиды можно найти по фор- муле:
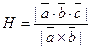 . (12)
. (12)
Рассмотрим примеры:
1. Найти объём треугольной пирамиды с вершинами
в точках 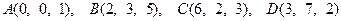
и найти её высоту, опущенную на грань 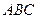 .
.
Найдём координаты трёх векторов, выходящих из одной точки, на которых строится пирамида: 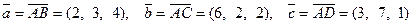 .
.
Тогда:
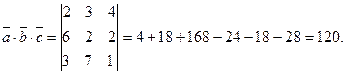
Таким образом, по формуле (11), объём пирамиды равен:
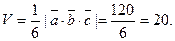
Чтобы найти высоту пирамиды, найдём векторное произве- дение:
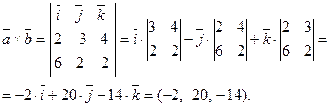
Отсюда 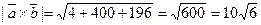 .
.
Тогда, по формуле (12)
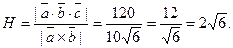
2. Проверить, что точки
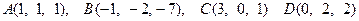 лежат в одной плоскости.
лежат в одной плоскости.
Если данные точки лежат в одной плоскости,

 С
С
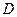
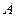
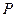
то векторы 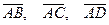 компланарны. Найдём координаты этих векторов:
компланарны. Найдём координаты этих векторов:
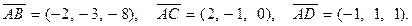
Векторы компланарны, если их смешанное произведение рав- но нулю, т.е. должно быть выполнено равенство:
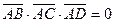 .
.
Найдём это смешанное произведение по формуле (10):
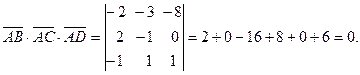
Смешанное произведение равно нулю. Следовательно, точки лежат в одной плоскости.
3. Поверить, что векторы 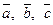 образуют базис и найти разложение вектора
образуют базис и найти разложение вектора  в этом базисе:
в этом базисе:
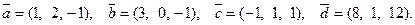
Если векторы образуют базис, то их смешанное произведе- ние 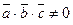 . В нашем случае:
. В нашем случае:
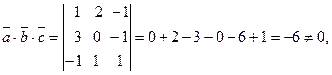
следовательно, векторы образуют базис
Тогда  представляет собой разложение вектора
представляет собой разложение вектора  в этом базисе. Найдём коэффициенты этого разло- жжения, для чего запишем соответствующее векторное равен -ство:
в этом базисе. Найдём коэффициенты этого разло- жжения, для чего запишем соответствующее векторное равен -ство:
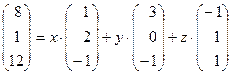 .
.
Учитывая правила действий с векторами, получим систему:
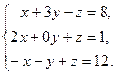
Решим данную систему линейных уравнений методом Гаусса. Запишем расширенную матрицу системы и получим нули ниже главной диагонали.

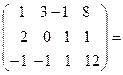
Умножим первую строку на (-2) и прибавим к второй строке и просто прибавим её к третьей строке. Получим:

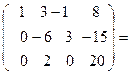
Умножим третью строку на ( 3) и прибавим к второй, после че- го разделим вторую строку на (3), а третью на (2) и поменя -ем их местами:


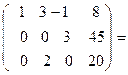
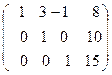 .
.
Получили систему:
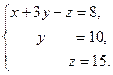
Таким образом:  Тогда
Тогда
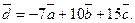
§ 4 ПОНЯТИЕ ЕВКЛИДОВА ПРОСТРАНСТВА
Изучая геометрические векторы, мы установили взаимно од- нозначное соответствие между направленными отрезками и упо- рядоченными наборами чисел (координатами векторов). При этом сложение векторов и умножение их на число производит- ся покоординатно. Обобщим вышесказанное следующим обра – зом: упорядоченная совокупность  чисел
чисел
