Кинематика поступательного движения
1.1. Материальная точка движется вдоль прямой так, что ее ускорение растет линейно и за первые 10с достигает значения 5 м/с2. Определить в конце десятой секунды: 1) Скорость точки, 2) Пройденный точкой путь. Ответ: V=25 м/с, S=83,3 м.
1.2. Точка движется по окружности радиусом 4 м по закону S=A + Bt2, где S – пройденный путь, А=8 м, В=2 м/с2, t- время. Определить, в какой момент времени нормальное ускорение равно 2 м/с2. Найти скорость, тангенциальное и полное ускорение точки в этот момент времени. Ответ: t=0,7с, at =4 м/с2, V=2,8 м/с, a=4,5 м/с2 .
1.3. Зависимость пройденного телом пути от времени задается уравнением S = A – Bt + Ct2 + Dt3, где А= 6 м, В=3м/с, С= 2 м/с2, D=1 м/с3. Определить для тела в интервале времени от t1=1с до t2= 4с: 1)Среднюю скорость движения, 2) Среднее ускорение. Ответ: V=28 м/с, а = 19 м/с2.
1.4. Движение точки задано уравнением х = Аt + Вt2, где А= 4 м/с, В = - 0,05 м/с2 . Построить графики зависимости пути, перемещения, скорости и ускорения точки в интервале времени от t1=0 до t2= 80 с.
1.5. При движении тела в плоскости xoy вектор скорости изменяется по закону V= 3ti – 4tj. Найти: 1) Перемещение тела за первые 4 с движения, 2) Ускорение, 3) Уравнение траектории, 4) Направление движения. Ответ: ∆r= 40 м, а= 5 м/с2, y = -1,33x, α = 530 .
1.6. Движение материальной точки задано уравнением r (t)= A(i∙cosωt + j∙sinωt) где r – радиус-вектор точки, А= 0,5 м, ω= 5 рад/с. Найти уравнение и начертить траекторию движения точки, определить модуль скорости и модуль нормального ускорения. Ответ: x2 + y2 = 0,25, V= 2,5 м/с, аn = 12,5 м/с2.
1. 7. Точка движется в плоскости XOY по закону: х=0,1∙sinωt, y=0,l∙(l+cos ωt). Найти путь, пройденный точкой за 10с, угол между векторами скорости V и ускорения а, уравнение траектории движения y=f(x).
Ответ: S(10)= ω; α=π /2; х2+(у-0,1)2=0,01.
1.8. Радиус-вектор частицы определяется выражениемr= 3t2i + 4t2j + 7k, где I, j, k- единичные вектора осей Х, Y, Z. Вычислить: 1) Путь S, пройденный частицей за первые 10с, 2) Модуль перемещения ∆r за тоже время, 3) Ускорение частицы. Ответ: S=500м, ∆r=500м, а=10 м/с2.
1.9.Точка движется в плоскости XOY по закону: x=2sin ωt; у =2cos ωt. Найти путь, пройденный телом за 2с; угол между векторами скорости V и ускорения а; траекторию движения y=f(x).
Ответ: S(2)=4ω; α=π/2; х2+у2=4.
1.10. Радиус-вектор, определяющий положение движущейся частицы, изменяется по закону: r = 2t√t∙i + 4t√t∙j. Найти для этой частицы скорость, путь и перемещение спустя 2 с после начала движения. Ответ: V=9,5 м/с, 12,6 м.
1.11. Точка движется так, что вектор её скорости V меняется со временем по закону V = 2 i + 2tj + 2t2k (м/с). Найти модуль перемещения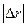 
за первые 4с её движения; модуль скорости в момент времени t=4c.
Ответ: 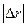= 46,3 м; V = 33 м/с.
1.12. Точка движется в плоскости XOY по закону: х = - 2t; у = 4t(l -t). Найти уравнение траектории у = f(x) и изобразить ее графически; вектор скоростиv и ускоренияа в зависимости от времени; момент времени t0, в который вектор ускоренияа составляет угол π/4 с вектором скорости v. Ответ: у = -х2-2х; V=-2i+4(1-2t)j, a=-8j, t0=0,75c.
1.13. Радиус-вектор частицы изменяется по законуr = t2i + 4tj - 2k (м). Найти вектор скорости v, вектор ускорения а; модуль вектора скорости v в момент времени t = 2с. Ответ: V = 2ti +4j, a=2i, 5,7 м/с.
1.14. Точка начинает двигаться по плоскости XOY из начала координат с ускорением а = 2i +3tj. Найти вектора скорости и ускорения в зависимости от времени и уравнение траектории Y(x). Ответ: V=2ti + 1,5t2j , r= t2i+ 05t3j, Y= 0,5x1,5.
1.15. В течение времени τ скорость тела задается уравнением V= A+ Bt + Ct2 (0 ≤ t ≤ τ). Определить среднюю скорость движения и среднее ускорение за промежуток времени от начала движения до τ. Ответ: V= А + Вτ/2 + Сτ2/3, а= В + Сτ.
1.16. Точка движется в плоскости XOY по закону: х = 2t; у = 4t(t - 1). Найти уравнение траектории у = f(x) и изобразить ее графически; вектор скорости v и ускорения а в зависимости от времени; момент времени t0, в который вектор ускорения а составляет угол π/6 с вектором скорости v. Ответ: у = х(х-2); V = 2i + (8t-4)j, a = 8j, t0=0,93c.
1.17. Точка движется в плоскости XOY по закону: x=10cos ωt; y=10(l-sin ωt). Найти путь, пройденный точкой за первые 10 с движения ; угол между векторами скорости V и ускорения а; уравнение траектории движения y=f(x).Ответ: S=100ω; α=π /2; х2+(10-у)2=100.
1.18. Точка движется так, что ее вектор скорости меняется со временем по закону V= 2 i + 4tj + 5t2k (м/с). Найти модуль перемещения точки за первые 2с её движения и модуль скорости в момент времени t=2c. Ответ: 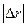= 16 м; V = 21,6 м/с.
1.19. Радиус-векторrчастицы меняется со временем по закону r= b∙t(1-αt), где α- постоянная, b-постоянный вектор. Найти: 1) Вектор скорости и ускорения частицы в зависимости от времени, 2) Промежуток времени ∆t, по истечение которого частица вернется в исходную точку, 3) Путь, который пройдет точка за время ∆t. Ответ: V= b(1-2αt), a= -2αb, ∆t=1/α, S= b/2α.
1.20. Точка движется в плоскости XOY по закону: х = t/2 ; у = t(l - t). Найти уравнение траектории у = f(x) и изобразить ее графически; вектор скорости v и ускорения а в зависимости от времени; момент времени t0, в который вектор ускорения а составляет угол π/3 с вектором скорости v. Ответ: у=2х-4х2; t0=0,64c.
1.21. Частица движется так, что ее радиус-вектор изменяется по закону: r = 7i + 4tj + 3t2k (м). По какому закону изменяется вектор скорости V и вектор ускорения а частицы? Найти модуль вектора скорости v в момент времени t = Зс и перемещение тела за первые 4с движения.
Ответ: V=18,4 м/с; ∆r = 50,6 м.
1.22. В плоскости xoy движется точка так, что скорость ее изменяется по закону V= 0,2t∙( 6i + 8j). Определить: 1) Ускорение точки, 2) Скорость через 5 с после начала движения, 3) Перемещение за 5 с движения. Ответ: а= 2 м/с, V=10 м/с, ∆r= 25 м.
1.23. Точка движется в плоскости XOY по закону: x=0,lcos ωt; y= l - 0,lsin ωt. Найти путь, пройденный телом за 10с; угол между векторами скорости V и ускорения а; траекторию движения y=f(x). Ответ: S =ω; α=π /2; х2+(1-у)2=0,01.
1.24. Точка движется в плоскости XOY по закону: х = 10t; у = 9t(l - 2t). Найти уравнение траектории у = f(x) и изобразить ее графически; вектор скорости v и ускорения а в зависимости от времени; момент времени t0, в который вектор ускорения а составляет угол π/3 с вектором скорости v. Ответ: у=0,9х(1-0,2х); t0=0,41c.
1.25. Частица движется по оси Х так, что ее скорость меняется по закону V=α√х, где α- постоянная. Имея в виду, что в момент времени t=0 частица находится в точке Х=0, найдите: 1) Зависимость от времени скорости и ускорения частицы, 2) Среднюю скорость частицы за время, в течение которого она пройдет первые S метров пути. Ответ: α2t/2, α2/2, Vср=α√S/2.
1. Кинематика поступательного движения
2. Кинематика вращательного движения
3. Динамика
4. Гармонические колебания
5. Затухающие колебания
6. Законы сохранения
7. Релятивистская механика
8. Статистические распределения
9. МКТ, идеальный газ
10. Явления переноса
11. Поверхностное натяжение
12. Первое начало термодинамики
13. Второе начало термодинамики