Переменной (формулировка)

1) ТЕОРЕМА: (о предельном переходе в неравенстве.).

Пусть при всех n выполняется неравенство 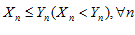,и переменные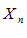 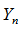и имеют пределы:

;

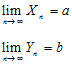Тогда: 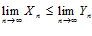, т. е. .

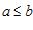Теорема означает, что в неравенстве можно переходить к пределам, сохраняя знак неравенства.

Доказательство:

Предположим, что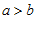

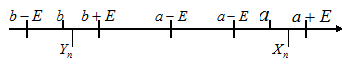
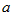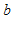Выделим вокруг точек и столь малые E– окрестности, чтобы они не пересекались.

По определению предела, начиная с некоторого номера n, переменные 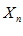и 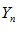попадут в свои E– окрестности предельных точек.

Это означает, что 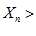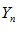, начиная с некоторого номераn,что противоречит условию. Противоречие доказывает теорему, ч. т. д.

Замечание:

Если при всех n выполняется 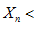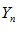(строго), то гарантировать строгого неравенства в пределе нельзя (в общем случае), гарантируется лишь нестрогое неравенство.

2) ТЕОРЕМА: (о сжатой переменной).

Пусть, начиная с некоторого 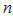, выполняются неравенства 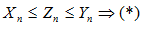, причем крайние переменные имеют одинаковый конечный предел 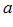, тогда переменная 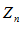также имеет предел, причем тот же самый.