Экспоненциальный закон надежности

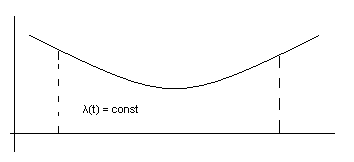
Часто надежность рассчитывается для периода нормальной эксплуатации, когда интенсивность отказов не зависит от времени λ(t) = const, тогда

p(t) = e- λt

(2.8)

Согласной этой формуле вероятность безотказной работы не зависит от того, сколько времени элемент проработал до рассматриваемого промежутка, а в формуле под временем t понимается продолжительность промежутка времени, для которого рассчитывается надёжность.

Определим вероятность безотказной работы в интервале (t, t+Δt) при этом предполагалось, что до времени t устройство проработало не отказав

p(t + Δt ) = e^{- λ(t + Δt)}= e^{- λt} e^{-λ Δt} = p (t) p(Δt/t)

где

p(t) - вероятность безотказной работы устройства для времени от 0 до t

p(Δt/t) - условная вероятность безотказной работы в интервале (t,t + Δt) при условии ,что элемент проработав время t не отказал

p(Δt/t) = e^{- λ Δt}

где

p(Δt/t) от времени t не зависит

Полученный экспоненциальный закон является частным случаем закона Пуассона

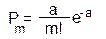
При m=0 , p = е, где m – число событий

По этому закону распределены редкие события законы (катастрофы)

Для систем содержащей К групп элементов с интенсивностями отказов λ1…..λ2… вероятность безотказной работы системы может быть записано

к P(t) = exp [ - ( N1λ1 + N2λ2 + ….+ Niλi+…+Nкλк )t ] = exp [ -t ∑ Niλi ]= i=1
к =∑ Niλi = λ0 i=1	(2.9)

Полученное выражение позволяет ориентировочно рассчитать значение вероятности безотказной работы системы за любой промежуток времени, если известны среднегрупповые значения интенсивности отказов элементов λi и число элементов в этих группах

Вероятность отказа стстемы

Q(t) = 1 –P(t) = 1 – e-Λ0t

(2.10)

Так как при экспоненциальном законе распределения времени исправной работы, среднее время безотказной работы

∞

Тср = То - ∫ p(t) dt

∞ Tcp = ∫ e-Λ0tdt = 1 /Λ0

(2.11)

Среднее время обратно пропорционально интенсивности отказов.

Так как в период нормальной эксплуатации надежность элемента не зависит от того, сколько времени он проработал, то замена элемента должна производиться только после отказов, т.к. вновь вводимые элементы вносят свой приработочные отказы.

Профилактическая замена элемента не только не повысит, но и понизит надежность, так как заменяемые элементы внесут свои приработанные отказы.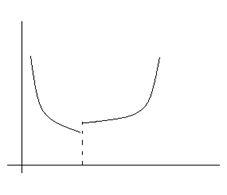

Только в конце срока эксплуатации, когда начинают сказываться износовые отказы, земена элементов может повысить надежность.