Підпослідовність числової послідовності

Нехай задана деяка послідовність . Розглянемо довільну зростаючу послідовність натуральних чисел . Виберемо з послідовності елементи з номерами , і розмістимо їх в тому самому порядкові, що і числа .

Одержана числова послідовність називається підпослідовністю послідовності . Можна встановити, що коли послідовність збіжна і має границею число 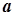, то будь-яка її підпослідовність також збіжна й має границею число .

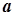3. Теорема Больцано-Вейєрштрасса

Теорема. Із будь-якої обмеженої послідовності можна виділити збіжну підпослідовність.

Доведення. Нехай послідовність обмежена, тобто існує такий відрізок 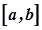, що для всіх 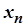виконується нерівність 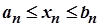. Поділимо відрізок 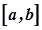пополам. Тоді принаймні в одній половині буде міститися нескінченна множина елементів послідовності . Позначимо цю половину 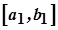. Поділимо тепер відрізок 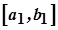на два рівних відрізки і знову виберемо той із них, у якому міститься нескінченна множина елементів послідовності . Позначимо його 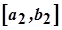. Продовжуючи цей процес, дістанемо послідовність укладених відрізків

,

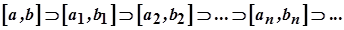у яких довжина 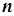-го відрізка 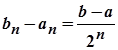прямує до нуля при 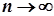. Отже, за теоремою про вкладені відрізки .

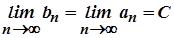Побудову підпослідовності 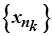послідовності виконаємо так: у значенні 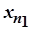виберемо довільний елемент із , який належить відрізку 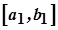, у значенні 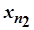- довільний елемент із , котрий належить відрізку 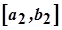і т. д. Оскільки для вибраних таким чином елементів виконується нерівність 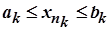, то за теоремою 2.7 .

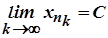4. Критерій Коші збіжності числової послідовності.

Означення границі числової послідовності не дає змоги встановлювати збіжність чи розбіжність числової послідовності, якщо не задано значення самої границі. Воно лише дає можливість перевіряти, чи є число 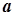границею даної послідовності, чи ні. Отже, виникає необхідність у наявності критерію збіжності числової послідовності, у якому б саме значення границі було відсутнє, тобто щоб цей критерій виявив "внутрішню" структуру збіжної послідовності. Такий критерій був установлений чеським математиком Больцано і французьким математиком Коші. Нині він має назву критерію Коші.

Теорема. Для того, щоб числова послідовність була збіжною, необхідно і достатньо, щоб для будь-якого числа 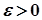існував номер 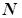такий, що нерівність

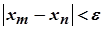(7)

виконувалася б для всіх 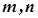, які одночасно задовольняють умову .

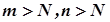Доведення. Необхідність. Нехай послідовність збіжна і 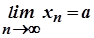. Задамо довільне число 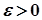. За означенням границі існує такий номер 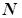, що

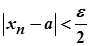(8)

для всіх 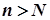. Зрозуміло, що коли 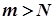, то для всіх таких 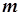нерівність (8) виконується. Отже, нехай 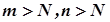. Тоді

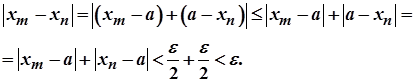
Необхідність доведено.

Достатність. Нехай для будь-якого 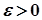існує номер 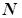, такий, що 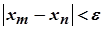для всіх 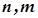, які одночасно задовольняють умову 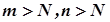. Доведемо, що при цьому послідовність збіжна. Нехай заданому 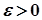відповідає номер 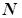, для якого виконується нерівність (7) для всіх 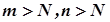. Зафіксуємо одне із значень 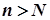. Тоді за умовою (7) виконуються нерівності

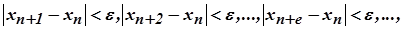
тобто всі члени послідовності, починаючи з 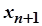, знаходяться в 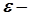околі фіксованої точки 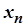. Звідси випливає, що послідовність обмежена. Отже, згідно з теоремою Больцано-Вейєрштрасса, із неї можна виділити збіжну підпослідовність 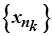. Нехай 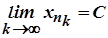. Тоді 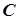є також границею послідовності . Дійсно, 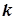можна вибрати настільки великим, щоб одночасно виконувались нерівності 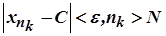. Тоді, поклавши 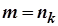, матимемо 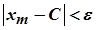і 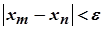. Звідси одержуємо

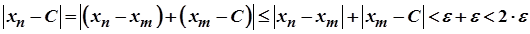
для всіх 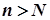. А це означає, що .

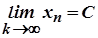Послідовність називається фундаментальною або послідовністю Коші, якщо для будь-якого числа 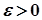існує номер 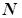такий, що для всіх 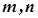, котрі одночасно задовольняють умову 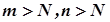, виконується нерівність .

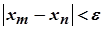ЛЕКЦІЯ 9

17. Поняття метричного простору.

18. Повні метричні простори. Теорема Бера.

19. Доповнення простору.

1. Поняття метричного простору

Означення метричного простору. Багато фундаментальних фактів математичного аналізу не пов'язані з алгебраїчною природою дійсних чисел, а спираються лише на поняття відстані.

Узагальненням уявлень про дійсні числа як про множину, в якій уведено відстань між елементами, є поняття метричного простору.

Метричним простором називається пара 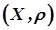, що складається з деякої множини 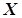елементів (точок) і відстані 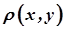– однозначної, невід'ємної функції, визначеної для будь-якої пари 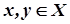, яка задовольняє наступні аксіоми:

1) 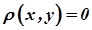тоді і тільки тоді, коли ;

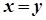2) 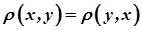(аксіома симетрії);

3) 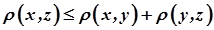(аксіома трикутника).

Сам метричний простір, як правило, позначається .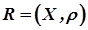

Множина дійсних чисел із відстанню

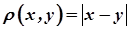
утворює метричний простір, що позначається .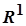

Виконання аксіом метричного простору для введеної таким чином відстані випливає із властивостей абсолютної величини дійсного числа.

Відкритою кулею 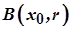у метричному просторі 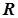називається сукупність точок 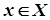, які задовольняють умову

.

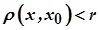Відкрита куля радіуса 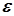з центром 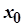називається 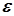-околом точки 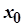і позначається .

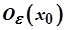У просторі 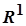відкритою кулею з центром 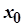є множина точок 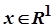, для яких виконується нерівність

,

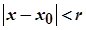а 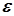− околом точки 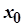є множина точок 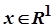, для яких

.

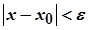Точка 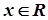називається точкою дотику множини 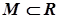, якщо будь-який її окіл містить хоча б одну точку з 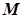. Сукупність усіх точок дотику множини 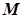позначається 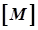і називається замиканням цієї множини.

Точка 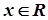називається граничною точкою множини 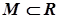, якщо будь-який її окіл містить нескінченно багато точок із .

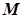Гранична точка може належати, а може і не належати .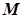

Точка 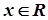називається ізольованою точкою множини 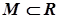, якщо вона належить 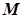і існує такий 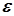-окіл точки 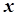, у якому немає точок із 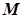, за винятком самої точки .

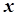Усяка точка дотику множини 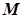є або гранична, або ізольована точка цієї множини.

Нехай 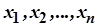– послідовність точок у метричному просторі 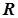. Говорять, що ця послідовність збігається в точці 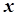, якщо 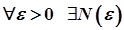таке, що .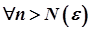

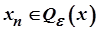Інакше це означення можна сформулювати так: послідовність збігається до 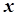, якщо .

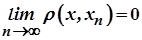Теорема. Щоб точка 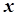була точкою дотику множини 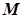, необхідно і достатньо, щоб існувала послідовність точок із 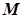, яка збігається до .

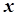Нехай 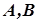– дві множини простору 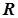. Множина 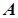називається щільною у 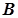, якщо 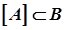. Зокрема, множина 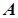називається скрізь щільною у просторі 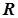, якщо .

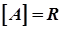Наприклад, множина раціональних чисел скрізь щільна на числовій прямій.

Множина 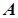називається ніде не щільною, якщо вона не щільна в жодній кулі, тобто в кожній кулі 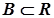існує інша куля 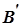, яка не має з 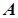жодної спільної точки.

Простори, в яких є злічена скрізь щільна множина, називаються сепарабельними.

Множина 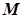метричного простору 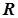називається замкнутою, якщо 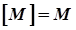, тобто якщо вона містить усі свої граничні точки.

Відрізок 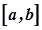числової прямої є замкнутою множиною.

Теорема. Переріз будь-якого скінченного числа замкнутих множин є замкнутою множиною. Сума будь-якого скінченного числа замкнутих множин є замкнутою множиною.

Точка 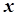називається внутрішньою точкою множини 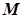, якщо існує окіл 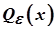цієї точки, який цілком міститься в .

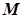Множина, всі точки якої − внутрішні, називається відкритою.

Інтервал 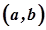числової прямої 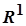є відкритою множиною.

Теорема. Щоб множина 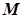була відкрита, необхідно і достатньо, щоб її доповнення 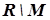до всього простору 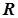було замкнутим.

Теорема. Об'єднання (скінченного або нескінченного) числа відкритих множин є відкритою множиною. Переріз (скінченного або нескінченного) числа відкритих множин є відкритою множиною.

Теорема 1.5. Усяка відкрита множина на числовій прямій є сумою (об'єднанням) скінченного або зчисленного числа інтервалів, які попарно не перетинаються (не мають спільних елементів).

Повні метричні простори.

Послідовність точок метричного простору називається фундаментальною, якщо вона задовольняє критерій Коші, тобто якщо 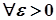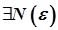таке, що

.

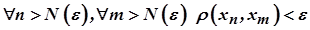Якщо в просторі 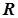будь-яка фундаментальна послідовність збігається, то цей простір називається повним.

Простір 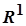дійсних чисел є повним.

Щоб метричний простір 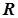був повним, необхідно і достатньо, щоб у ньому будь-яка послідовність укладених одна в одну замкнутих куль, радіуси котрих прямують до нуля, мала непорожній переріз.

Теорема Бера. Повний метричний простір не можна подати у вигляді об'єднання зліченного числа ніде не щільних множин.

Із теореми Бера зокрема випливає, що всякий повний метричний простір без ізольованих точок незліченний.

Доповнення простору.

Якщо простір 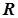не повний, то його завжди можна включити єдиним способом у повний простір.

Простір 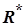називається доповненням метричного простору 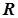, якщо:

1) 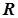є підпростором простору ;

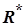2) 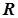скрізь щільний у 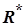, тобто .

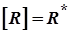Простір 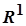усіх дійсних чисел є доповненням простору 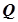раціональних чисел.

ТЕМА 3. ГРАНИЦЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ

ЛЕКЦІЯ 10

20. Границя функції. Означення границі функції в точці за Гейне й за Коші.

21. Односторонні границі.

22. Границя функції на нескінченності.

23. Теореми про границі функцій.