Инерциясыз (күшейткіш) буын

Инерциясыз деп, шығыс шамасы кіріс шаманы еш бөгетсіз және кешіктімей көрсететін буынды айтамыз

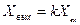(3.1)

мұндағы ­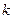- үзбенің күшею коэффициенті (беріліс коэффициенті)

Күшейткіш буынды кейде қатаң байланыс деп атайды. Өтпелі процесс күшею үзбесінде болмайды.

Күшейткіш буынның мысалдары: қатты рычак, инерциясыз электронды күшейткіш, электр машинасының бөлшектерінің механикалық мүшеленуі. (3.1) өрнегінен күшейткіш үзбенің беріліс функциясы

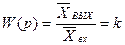(3.2)

Амплитудалы –фазалы сипаттаманың теңдеуі

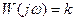(3-3)

Бұл жағдайда өсьтің оңбағытымен сәйкес келетін вектор (3-1. сурет, )

Айғақты және жорамал жиіліктік сипаттамалардың теңдеулері:

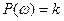-жиілік өсіне параллель сызық;

- жиілік өсіне сәйкес келетін сызық; (3.1. сурет, в)

Амплитудалы жиілік сипаттама

.

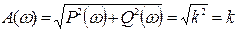Логарифмдік амплитудалы жиілік сипаттама

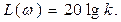
Логарифмдік фазалы жиілік сипаттама (3.1. сурет, в)

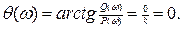
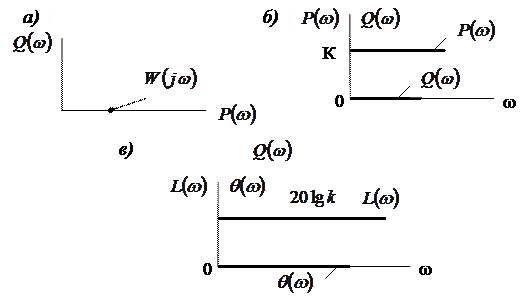
3.1. Сурет. Инерциясыз буынның жиілік сипаттамалары

Инерциялы буын

Инерциялы деп бірінші ретті буынды айтамыз, кірісіне сатылы әсерді берген кезде шама апериодты түрде ( экспоненциялы заң бойынша) жаңа орнатылған мәнге ұмтылады. Мұндай үзбені сонымен қатар инерциялы, статикалық , релаксациялы, бір сиымдылықты деп аталады.

Апериодты буындарға сиымдылық пен активті кедергіден тұратын электр тізбегі (сиымдылықсыз), массасы мен үйкеліс күші бар (серіппесіз) немесе серіппе мен үйкеліс күшінен (массасыз) тұратын механикалық құрылғылар және энергияның кез- келген түрі жинақтала алатын және оны тарата алатын басқа да ұқсас құрылығылар жатады.

Тербелмелі буын

Тербелістік деп (екі сиымдылықты) екінші ретті буын аталады, оның кірісіне сатылы әсерді алған кезде шығыс шама өшіп- жанатын тербеліс жасай отырып, жаңа орнатылған мәнге ұмтылады.

Тербелмелі буындарға екі энергетикалық сиымдылықтар арасындағы энергиямен алмасып, өтпелі режимдер ағып өтетін құрылығылар кіреді, мысалы, индукивтілік, сиымдылық және активті кедргіден құралған электр тізбегі массасы, серікпесі және үйкеліс күші бар механикалық құрығы; кинетикалық энергияны якорда және электрмагнитті энергияны магнитті тізбекте жинақтай алатын тәуелсіз әсерлі тұрақты токтың элекр қозғалтқышы, оның кіріс шамасы якорға қосылған кернеу, ал шығыс- якорьдың айналу жылдамдығы болып табылады (3.6. сурет, б)

Момент теңдеуімен жазылатын өтпелі процестегі қозғалтқышың іс-әрекетін қорастырайық

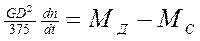(3.25)

және якорь тізбегіндегі Э.Қ.К-ң теңәсерлік теңдеуін қарастырамыз

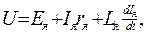; (3.26)

мұндағы 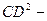якорьдың маховой моменті, н^*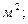

М_д-қозғалтқыштың айналу моменті,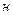

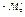
М_с –қозғалтқыш білігіндегі статикалық момент (кедергі моменті), ;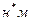

якорьдың айналу жылдамдығы об/мин;

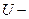якорға қосылған кернеу, в;

Е_я- якорьдың қарама-қарсы Э.Қ.К.

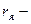якорь тізбегінің кедергісі (кернеудің қоректену кедегісін қосқанда), ал;

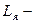якорь тізбегінің индуктивтілігі (кернеудің индуктивтігін қосқанда ),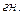

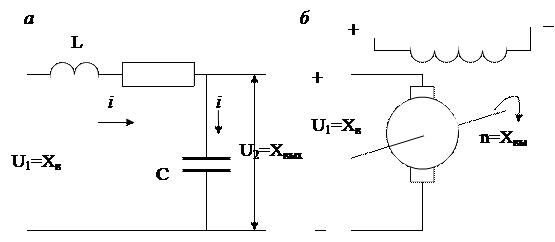
3.6. Сурет. Тербелістік буын мысалары:

активті кедергісі, индуктивтілігі және сиымдылығы бар тізбек;

б- тәуелсіз әсерлі тұрақты ток қозғалтқышы.

Қозғалтқыштың әсері тәуелсіз тұрақты болғандықтан, және сәйкесінше ағыны да тұрақты болса, онда Е_я қарама-қарсы Э.Қ.К-і айналу жылдамдығына пропорционалды.

Е_я=С_е^*n,

мұндағы С_е – конструктивті тұрақты, в *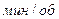

Е_я –(3.26) теңдеуін қоямыз.

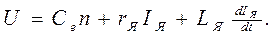(3.27)

Қозғалтқыштың айналу моменті мына өрнектен анықталады

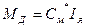(3.28)

мұндағы 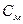-конструктивті тұрақты,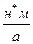

Кедергі момент шартты түрде кедергі моментке сәйкес 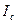-тогы арқылы көрсетуге болады.

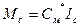(3.29)

(3.28) бен (3.29)-ды (3.25) қойып, мынаны аламыз.

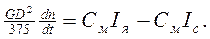(3.30)

Бұл теңдеуден якорь тогы мен оның туындысының мәнін табамыз

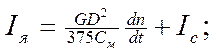
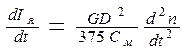
сөйтіп оларды (3.27)- теңдеуге қойып шығарамыз

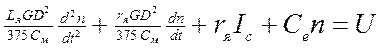(3.31)

(3.31) теңдеуді 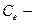ға бөліп, ал 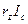мүшені теңдеудің оң жақ бөлігіне ауытыра және 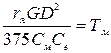- қозғалтқыштың электрмеханикалық уақыт тұрақтысын белгілей отырып, теңдеудің сол өлігіндегі бірінші мүшесін С_е –ге көбейтеміз және 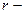ға бөлеміз.

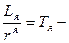қозғалтқыштың якорының тізбегінің уақыт тұрақтысы, сек

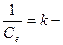қозғалтқыштың күшею коэффициенті (беріліс коэффициенті), 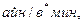мынаны аламыз

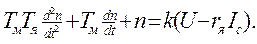(3.32)

Егер қозғалтқыш бос жұмыс істесе, онда

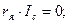
Қозғалтқыш теңдеуі операторлық түрдегі түрі

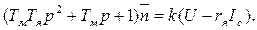(3.33)

Жалпылық үшін алмастырамыз

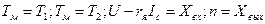
Тербелістік үзбе теңдеуінің жалпы түрде аламыз.

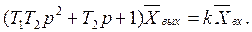(3.34)

(3.6), a- суретте келтірілген электр тізбегіндегі өтпелі прцестің теңдеуі де осындай боалды.

Бұл теңдеудің шешеімі:

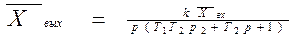
егер алымы мен бөлімін T₁, T₂-ге бөлгеннен кейін

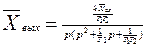(3.35)

Сипаттамалық теңдеудің түрін анықтаймыз

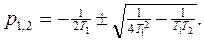(3.36)

Егер

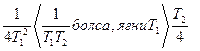
якорь тізбегінің үлкен электр магнитті инерциясына сәйкес келсе, онда түбірлері комплексті болады да,

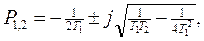
ал өтпелі процесі өшіп-жанатын тербелістермен орнатылған мәнге келетін тербелісті болып келеді. Өтпелі процестің уақыт бойынша теңдеуін алу үшін бейнесінің оригиналын тауып аламыз (3.35).

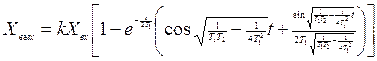
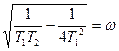деп алмастырып, мынаны аламыз.

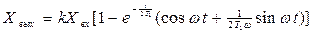
мұндағы өшіп қалған тербелістердің жиілігі

Өтпелі функцияның теңдеуін X_вх=1 деп қабылдап аламыз.

(3.37)

Бұл формуланы қолдану үшін барлық түрлендіруді жасау қажет емес. Сипаттамалық теңдеулердің түрін тапқан жөн, олардың комплексті екеніне көз жеткізе отырып, оригинал формуласына дифференциялды теңдеулерге уақыт тұрақтысының мәндерін қойған жөн. (3.37) теңдеуі бойынша құрылған үзбенің өтпелі функциясының графигі 3.7, а- суретте көрсетілген.

Осы үзбенің 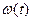салмақтық функциясын алу үшін (3.37) өрнегінің туындысын аламыз. Салмақтық функцияның графигі 3.7, в-суретте бейнеленген.

Енді сипаттамалық теңдеулердің түбірлері айқын және әртүрлі болатын шарттардағы (3.35) өрнегінің оригиналын табамыз

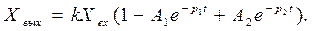
X_вх=1 деп қабылдап, өтпелі функция теңдеуін аламыз.

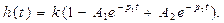(3.38)

Бұл екі экспоненттің қосындысымен берілетін опериодты процестің теңдеуі. Мұндай үзбені екінші ретті апериодты үзбе деп атаймыз және ол тербелісті үзбеден айырмашылығы, тізбектей қосылған бірінші ретті екі апериодты үзбеге бөліне алады. (3-38) түрдегі теңдеу бойынша құрылған өтпелі функцияның графигі 3-7, б-суретте бейнеленген. Бұл үзбенің салмақтық функциясын (3-38),өрнегінің туындысы ретінде аламыз.

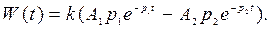
Негізгі әдебиет: 1 [65-105]

Қосымша әдебиет: 1 [92-122]; 2 [135-164]

Бақылау сұрақтар:

1. АБЖ қандай тәсілдермен жеке бөлшектерге бөлуге болады?
2. Инерциясыз буын (ПФ, ЧХ, ПП).
3. Инерциялы буын (ПФ, ЧХ, ПП).
4. Тербелмелі буын (ПФ, ЧХ, ПП).
5. Параметрлерінің әртүрлі қатынастары кезінде тербелмелі буынның өтпелі процесі қандай түрге ие болуы мүмкін?

№ 3 – Дәрістің конспектісі

Дәрістің тақырыбы: АРЖ–ң типтік үзбелері, беріліс функциялары мен жиіліктік сипаттамалары. (жүйе элементрерін типтік динамикалық үзбелерге жіктеу әдісі. Типтік үзбелер – инерциясыз, І ретті инерциялы және тербелістік, интегралдаушы, дифференциалдаушы және кешігу үзбелерінің беріліс функциясын және жиілік сипаттамасының аналитикалық өрнегін анықтау).

Интегралдаушы буын

Интегралдаушы деп шығыс шаманың өзгеру жылдамдығы кіріс шамаға пропорционал, немесе шығыс шамасы, сол шаманың, уақыт бойынша интегралына пропорционал болатын үзбені айтамыз. Мұндай үзбені сонымен қатар астатикалық немесе бейтарапты буын айтады.

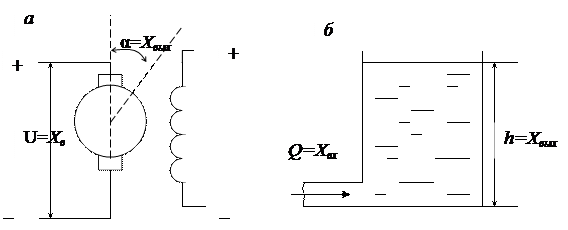
3.10. Сурет. Интегралдаушы үзбе мысалдары

Тамаша және айқын интегралдаушы үзбелер деп ажыратылады. Тамаша интегралдаушы үзбеге мысал болып тәуелсіз әсердегі тұрақты токтың электрлі қозғалтқышы бола алады, егер кіріс шама ретінде 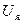якордың кернеуін, ал шығыс деп – якордың бұрылу бұрышын есептеуге болады, бұл кезде электромеханикалық және электромагнитті уақыт тұрақтылары қатысы аз және оларды елемеуге болады (3.1. сурет, а).

Басқа мысал болып сұйық келіп түсетін резервуар болып табылады, егер қоректену құбырдағы сұйықтың жылдамдығы, лезде орнықты мәнге жеткен кезде кіріс шама деп Q сұйық ағынын, ал шығысын – резервуардағы сұйықтың деңгейін санағанда (3.1. сурет, б).

Көбінесе тәжірибелік есептеулердің жиілікті дәлдігімен айқын интегралдаушы үзбелердің орнына тамаша үзбелерді қабылдауға болады, сондықтан осы екі түрін де қарастырамыз.

Тамаша интегралдаушы үзбе ретінде тұрақты ток, қозғалтқышын қарастырамыз (3.1. сурет, а). Қозғалтқыштың айналу жылдамдығы мына өрнектен анықталуы мүмкін:

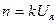(3.1)

мұндағы k–беріліс коэффициенті.

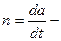ны (3–1) – өрнегіне қойып, мынаны аламыз:

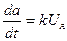(3.2)

мұндағы – қозғалтқыш білігінің бұрылу бұрышы.

Бұл өрнекті интегралдаймыз:

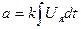(3.3)

(3.2) және (3.3) өрнектерг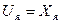е және 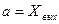–деп алмастырып, (3.2) және (3.30) мынаны аламыз:

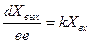
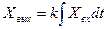(3.4)

Бастапқы нөльдік шарттардағы операторлы түрдегі (3.40) теңдеуі мына түрге келеді:

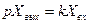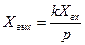және (3.5)

Бейнесінен оригиналға өтіп, 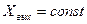кездегі шығыс шаманың уақыт бойынша өзгеру заңдылығын анықтаймыз

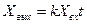(3.6)

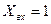деп қойып, өтпелі функцияның теңдеуін аламыз 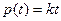. Бұл теңдеу 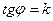бұрыштық коэффициентті анықтаймыз

Интегралдаушы үзбенің беріліс функциясын (3.5) өрнегінен аламыз:

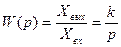(3.7)

Амплитудалы – фазалы сипаттма теңдеуі:

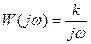(3.8)

Бұл жорамал саннан құтылып, айғақ және жорамал жиілікті сипаттамалардың теңдеулерін табамыз:

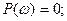(3.9)

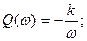(3.10)

бұл сипаттамалар осы теңдеулер бойынша тұрғызылған (3.3. сурет, б).

Амплитудалы және фазалы жиіліктік сипаттама теңдеулері:

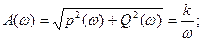(3.11).

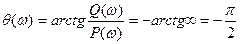(3.12)

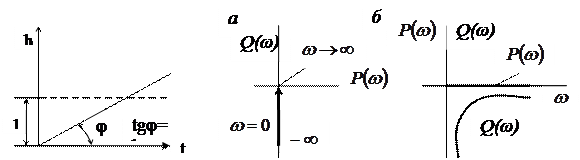
3.2. Сурет. Идеалды интегралдаушы 3.3. Сурет. Идеалды интегралдаушы үзбенің

үзбенің өтпелі функциясының графигі жиіліктік сипаттамалары

Логарифмдік амплитудалы жиіліктік сипаттаманы (3.11) өрнегін логарифмдей отырып аламыз:

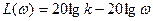(3.13)

Жиіліктің барлық диапазонында бұл сипаттама 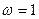абсцисалы және 20 lg k ординаталы және –20 дб/дек еңгіштігі бар нүкте арқылы өтетін түзуді береді (сурет. 3-4).

Логарифмді фазалы жиіліктік сипаттама абсцисса өсіне паралель және одан 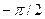қашықтықта қалып қойған түзумен бейнеленеді.

Дифференциалдаушы буын

Дифференциялдаушы деп шығыс шама кіріс шаманың өзгеру жылдамдығына пропорционал, яғни оның туындысына пропорционал буынды айтамыз.

Дифференциалдаушы буындарға мысалдар болып мыналар бола алады: серіппелі гидравликалық тыныштандырғыш (сурет. 3–7, а) трансформато (сурет. 3–7, б); активті кедергісі мен сиымдылығы бар тізбек (сурет. 3–7,в); активті кедергі мен индуктивті тізбек (сурет. 3–7, ).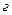

Тамаша дифференциялдаушы үзбелер деп жоғарыда қарастырылған барлық құрылғыларды санауға болады, егер онда активті электрлі кедергілер мен үйкеліс күштерімен елемеуге болса (в механикалық құрылғыларда).

Тамаша дифференциялдаушы үзбенің дифференциялдық теңдеуі мына анықтамаға сәйкес.

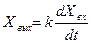
Немесе операторлық түрде

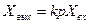(3.22)

Кірісіне сатылы әсерді берген кезде шығыс шаманың өзгерісі мен өтпелі функциясы келесі түсініктер ден анықталуы мүмкін. Сатылы кіріс функция, үзіліс сияқты, дифференциялданбайды, бірақ кіріс шаманы сатыдағы өзгеріс жылыдамдығы шексіздікке тең, өйткені кіріс шаманың соңғы өзгеруі нольге ұмтылатын уақыт шегінде жүреді. Ал дифференциялдаушы үзбенің шығыс шамасы кірістің өзгеру жылдамдығына пропорционал болғандықтан, тамаша үзбедегі кірісіне сатылы әсер берген кезде шығыс шамасы нольге тең уақыт моментінде шексіздікке дейін шолп– шолп береді, ал содан кейін нольге айналады, өйткені кіріс шаманың өзгеру жылдамдығы барлық тізбекті моменттерде нольге тең болады (сурет. 3–8).

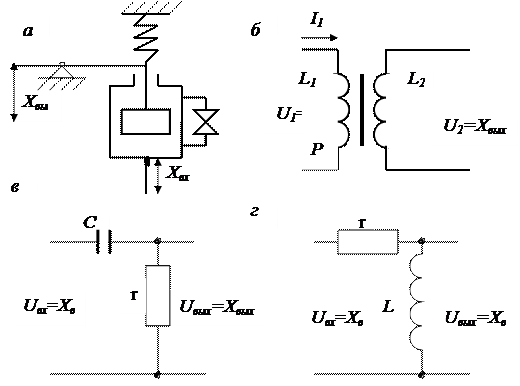
3.7. Сурет. Дифференциялдық үзбенің мысалдары

Тамаша дифференциялдаушы үзбенің (3.22) өрнектен алынған беріліс функциясы.

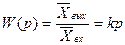(3–23)

Амплитудалы – фазалық сипаттаманың теңдеуі

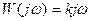(3.24)

ал сипаттаманың өзі жорамал өсьтің оң бағытымен сәйкес келетін түзумен беріледі ( 3.9. а. сурет).

(3.24)–тен тікелей айғақты және жорамал жиіліктік сипаттмалар теңдеулерін тауып аламыз

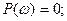
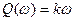. (3.25)

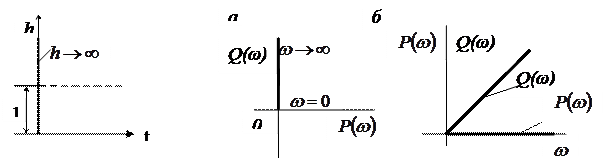
3.8. Сурет. Идеалды дифференциялды 3.9. Сурет. Идеалды дифференциялдаушы

буынның өтпелі процесінің графигі буынның жиілікті сипаттамалары

Бұл сипаттаманың графиктері 3–9, б–суретте келтірілген.

Амплитудалы және фазалы жиіліктік сипаттамалар теңдеуі

; (3.26)

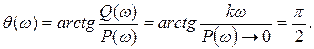(3.27)

Логарифмді амплитудалы жиіліктік сипаттама теңдеуін (3.26) өрнегін логарифмдеп аламыз.

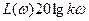(3.28)

Бұл абсциссасы 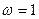және ординатасы 20 lg k нүктесі арқылы өтетін 20 дб/дек еңгіштіктегі түзу логарифмді масштабта. (3–10. сурет) Логарифмді фазалы жиіліктік сипаттама (3.27) өрнегіне сәйкес, жиілік өсіне параллель және одан 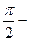ге қалып қоятын түзуді береді (3.10. сурет).

Екінші орамның магниттеу әсері мен кернеудің ондағы активті түрде төмендеуімен шааырауын елемей трансформатордағы қтпелі процесті қарастырамыз. Бұл трансформато бос жүріс режимге жақын режимде жұмыс істеген кезде мүмкін болады.

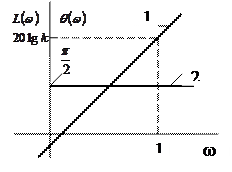
3.10. Сурет. Тамаша дифференциалдаушы үзбенің логарифмдік жиіліктік сипатттамалары:

1– амплитудалы; 2– фазалы.

Негізгі әдебиеті: 1[65-104]; 2[170-197].

Қосымша әдебиеті: 1[92-122]; 2[135-164]

Бақылау сұрақтар:

1. Интегралдайтын буын (ДТ, БФ, ЖС, ӨП).
2. Дифференциалдайтын буын (нақты, идеалды және олардың ДТ, БФ, ЖС, ӨП).
3. Кешігу буыны (буын теңдеуі, БФ, ЖС).
4. ТДБ ЖС аналитикалық өрнектерін және олардың БФ анықтау.
5. АФЖС құру тәсілдері.

№ 4 Дәрістің конспектісі

Дәрістің тақырыбы: Типтік динамикалық буындардың қосылуы. Жүйенің операторлық өрнегі. Жүйенің сипаттамалық теңдеуі.

Автоматты ретту жүйесін зерттеу және есептеу кезінде ондағы өтетін физикалық процестің математикалық бейнесінен шығады. Әдетте бұл өрнек айнымалы шамалар мен олардың туындысы арасындағы байланысты беретін дифференциялды теңдеулер жүйесі түрінде беріледі. Мұндай тәсіл, теңдеу зерттелетін жүйенің толық әрекетін бейнелегенде, математикалық жақтан аса жалпы болып табылады және барлық жағдайларда қолданылады.

Онымен қатар, автоматты басқару жүйесінің үлкен класы үшін (сызықтық жүйе) басқа тәсіл де қолданылады, ол операторлық әдісті пайдаланумен байланысты. Бұл тәсіл кезде зерттелетін жүйе сигналды тек бір бағытта: кірістен шығысқа беру қасиеті бар бағытталған әрекеттегі үзбелі бөліктерге бөлінеді. Бұл үзбелердің жиынтығы олардың арасындағы байланыс желілерімен біріккен, ол байланыс олардың өзара әрекетін сипаттайтын басқару жүйесінің құрылымдық схемасын құрайды.

Функционалды мен құрылымдық схемалар арасында нақты жалпылығы бар – сол және басқалары ақпараттарды басқыру жүйесінің тұйықталған контурында беру мен өңдеу процесін береді. Дегенмен олардың арасында анық ерекшелікте бар: функционалды схемалар жүйені оған кіретін элементтердің құрамы бойынша сипаттайды, ол олардың қойылымдары бойынша, яғни олармен орындайтын функциялары бойынша қарастырылады; бағытталған әрекеттегі үзбелерден тұратын құрылымдық схемалар жүйенің математикалы түрдегі динамикалық қасиеттерін бейнелеп береді. Жүйенің құрылымы мен оған кіретін функционалды элементтердің түрінен жүйені бағытталған әрекеттегі үзбелерге, сол үзбенің әр қайсысы үшін беріліс функциясын үзбенің шығыс шамасының операторлық бейнесінің кіріске қатынасы ретінде анықтау өте оңай болуы мүмкін және жеке үзбелерді бір – бірімен байланыс желісімен қосуға болатындай етіп бөлуге болады.

Бағытталған әрекеттегі әрбір үзбенің беріліс функциясы операторлы түрде жазылған және берілген үзбенің дифференциялды теңдеудегі шығыс шаманың бейнесіне қатысты рұқсат етілген түрде болып келеді. Осылай, автоматты басқару жүйесінің дифференциялдық теңдеуін толық құру есебі жеке үзбелердің теңдеуін құруға алып келеді. Осы кезде алынған ұтыс еңбек өнімділігі жағынан аса шын анық бола бастайды, өйткені тәжірибеде көп жағдайларды автоматты басқару жүйесінің құрылымдық схемасы бағытталған әрекеттегі типтік үзбелері деп аталатын әртүрлі комбинацияларды береді, оның беріліс функциялары мен қасиеттері бір және мәңгілікке жасалуы мүмкін.

Құрылымдық схеманың аса маңызды ерекшелігі олардың физикалық көрнектілігі болып табылады, ол зерттелетін жүйеде жүретін процестер жөніндегі дифференциялды теңдеуінің жалпы түрде жазылуымен салыстырғанда аса нақты болжамдар береді.

Айтылғандардан автоматты басқа жүйесін бағытталған әрекеттегі үзбелерге бөлу мен басқару жүйесінің принциптік пен функцияналды схемаларға негізделе отырып жалпы түрде құрылымдық схемаларды құру қажет екені түсінікті.

Құрылымдық схема салынғаннан және оларға кіретін үзбелердің беріліс функциясын алғаннан кейін барлық жүйенің беріліс функциясын анықтау қажет. Бұл кезде, егер юасқару жүйесін бағытталған әрекеттегі үзбелерге бөлу үшін қандай да бір бірыңғай рецеп беруге болмайды, ол әр кез жалпы тәртіп пен интуиция ұғымдарын едәуір мөлшерде басқарушылық ету қажет, ұғымдар тәжірибе жинау мен арнайы тапсырмаларды орындау процесінде алынған, онда жүйенің беріліс функциясын оның құрылымдық схемасы бойынша анықтау үшін құрылымдық схеманы түрлендірудің арнайы ережелерін пайдалануға болады, төменде негізгілері келтірілген.

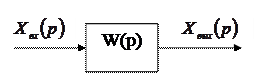
4.1. Сурет. Бағытталған әсер жүйесі

Бағытталған әрекет ететін қасиеті бар ажыраған жүйені қарастырамыз (4.1. сурет). Бұл бір үзбе сияқты, олардың кез – келген комбинациясы бола алады.

Беріліс функциясын анықтау бойынша

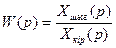(4.1)

осыдан бағытталған жүйенің негізгі қасиеті шығады

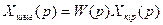(4.2)

яғни шығыс шаманың операторлық бейнесі кіріс шаманың бейнесіне көбейтілген жүйенің беріліс функциясына тең болады.

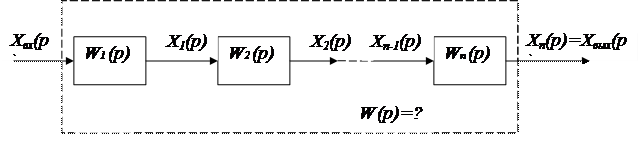
4.2. Сурет. Бағытталып әрекет ететін буынның тізбектей қосылуы

Бағытталған әрекетті буындарды қосудың негізгі жағдайларын қарастырайық.

1.Тізбекьеп қосылу (бірконтурлы ажыратылған жүйе). Құрылымдық схемасы 4.1 – ші суретте келтірілген.

(4.2) формула негізінде ң әрқайсысы үшін былай жазуға болады.

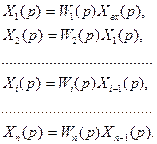
Барлық аралық шамаларды жоя отырып, яғни алдыңғыларды келесіге қоя отырып, соңғы мүше үшін өрнегін аламыз: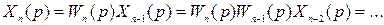

Соңғы ші үзбенің шығысы бір уақытта жүйенің шығыс шамасы болып табылады, яғни:

;

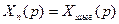аламыз

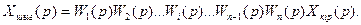
Анықталуы бойынша

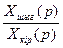
қатынасы 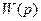жүйесінің беріліс функциясы болғандақтан, соңында алатынымыз

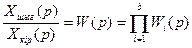(4.3)

Сонымен, бағытталған әрекеттегі тізбектей есептелген үзбелердің беріліс функциясы жеке үзбенің функцияларының туындысына тең болады.

2.Паралельді келісілген қосылу. Бағытталған әрекеттегі үзбелердің паралельді келісілген қосылуы деп жүйенің кіріс шамасы барлық үзбелер кірісіне параллельді берілетін, ал олардың шығыс шамасы жүйе шығысында алгебралы түрде қосылады.

2.3. Сурет. Бағытталған әрекеттегі үш үзбелердің параллельді қосылуының жеке жағдайы берілген.

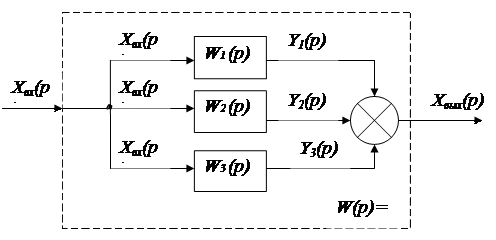
4.3. Сурет. Бағытталатын әрекеттегі үзбелердің параллельді келісілген қосылу

(4.2) формула негізінде параллельді қосылған үзбелердің әрқайсысы үшін былай болады:

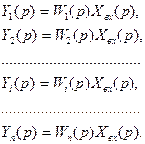
Жазылған теңдіктерді қосып, оларды ескере отырып, бағытталған әрекеттегі параллель келісілген қосылуды анықтау бойынша сол жақ бөлігінің соммасы жүйенің шығыс шамасы болып табылады, сонда аламыз

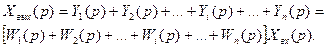
(4.1) беріліс функцияны анықтауға сәйкес (2.1) соңғы өрнектен мынаны аламыз

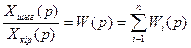(4.4)

Осылай, бағытталған ірекеттегі келіспіп паралельді қосылған үзбелердің беріліс функциясы жеке үзбелердің беріліс функциясының алгебралық соммасына тең.

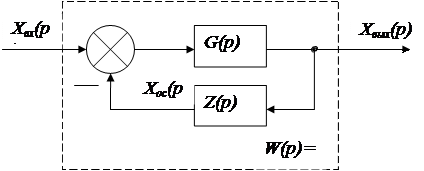
4.4. Сурет Бағытталған әсерлі қарсы параллельді қосылған буындар (кері байланыс)

3.Параллельді қарама – қарсы қосылу (кері байланыс). Алдымен негізгі жағдайды – теріс кері байланысты қарастырамыз.

G(p) мен Z(p) беріліс функциялары бағытталған әрекеттегі қарапайым үзбелерге де, және олардың кез – келген комбинацияларына да сәйкес болуы мүмкін.

Сурет. 2.4. Бейнеленген схема үшін,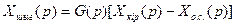

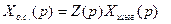
Олардың X_о.с. аралық шамасын алып тастап тұйықталған жүйенің беріліс функциясын аламыз

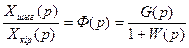(2.5)

мұндағы

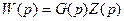
бұл ажыратылған жүйенің беріліс функциясы. Соңғы айтылғанның мәні түсінікті, егер ойымызша ажыратылған басқару контуры кез келген орында және, оны “түзетіп”, ажырау орнына берілген сигналдың өтуін қарастыру, ол тізбектеліп қосылған үзбелердің тізбегі бойынша қосылған.

Сонымен, автоматты тұйықталған басқару жүйесінің беріліс функциясы бірге жоғарлаған тіке тізбектің беріліс функциясының ажыраған жүйенің беріліс функциясына қатынасына тең болады.

Бұл нәтиже (4.5) формуласы сияқты тең айта кеткен жөн, ол сыртқы әсер басқару жүйесінің кірісіне келіп түскен 4.4– суретте берілген жағдайда ғана әділетті сондықтан 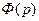–ны кейде тұйықталған жүйенің кіріс әсері бойынша беріліс функциясы деп атайды.

Шындығында, басқарушы кіріс әсерден бөлек нақты жүйе әртүрлі қоздырушы әсерлерге душар болады (жүктеменің тербелуі, элементтің сипаттамаларының тұрақсыздығы, бөгеттер және т.б.), олар жүйеге кез – келген жерде келіп түсе алады.

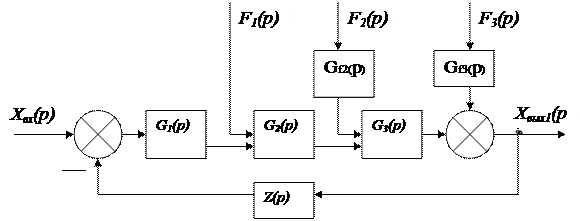
4.5. Сурет. Жүйенің құрылымдық схемасы

4.5. суретте берілген автоматты басқару жүйесінің құрылымдық схемасын қарастырайық. Жүйенің тіке тізбегі берілсін G1(p), G2(p), G3(p) функциялары бар бағыттағы әрекеттегі тізбектеп қосылған үзбелерден тұрады. Соңғы екі үзбенің кірістеріне алдыңғы үзбелердің шығыс шамаларына сәйкес қосылатын F1 (p) және F2 (p) қоздырушы әсерлер келіп түседі. Одан бөлек, F3 (p) әсері тікелей жүйенің шығыс шамасына әсер етеді, ол схемада арнайы соммалау элементімен бейнеленген. Осыдан F3 (p) әсерін қосу орны кері байланыспен қамтылғаны аса маңызды, яғни беріліс функциясы Z(p) үзбеге жүйенің шығыс шамасы ендігі F3(p) әсерін ескеріп келіп түседі. Кері жағдайда ешқандай реттеу әсері болмас еді, өйткені қоздырушы әрекеттің әсерінен тозған жүйенің басқару шамасы кері байланыспен түзетілмеген болар еді.

Құрылымдық схемадан (4.5. сурет) F2(p), F3(p) қоздырушы әсерлер жүйенің тіке түзбекті үзбелер кірісіне тікелей емес, ал беріліс функциялары Gf2 (p), Gf3 (p) бар қосымша үзбелер арқылы келіп түседі, олар жүйенің берілген шамасының нақты қоздырушы әсерден тәуелдену сипатын береді.

Қарастырылып жатқан басқару жүйесінің сызықтық күшіне басылу принципі қолданылады, ол жүйенің жалпы реакциясын сыртқы әсердің әрқайсынан жеке реакция соммасы ретінде анықтауға мүмкіндік береді.

X_кір (p) = 0; F2 (p) = 0, F3 (p) = 0 деп қойсақ және X_шыг (p) – ң тәуелділігін анықтаймыз.

G2 (p) үзбенің кірісіне G2(p), G3(p) үзбелері арқылы өте отырып F₁ (p)+ G₁ (p) 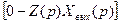, сигналдар сомасы әсер етеді, шығысқа береді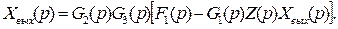

X_шыг(p)–ға қатысты соңғы теңдікті шешіп, аламыз 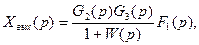(4.7)

мұндағы W(p)=G₁(p) G₂(p) G₃(p)Z(p) – ажыратылған жүйенің беріліс функциясы.

Алынған нәтижені келесі ереже түрінде қорытуға болады: жүйенің шығыс шамасының операторлы бейнеленуі алымы қосылу әсерінің нүктесі мен жүйе шығысы арасында тізбектеліп қосылған үзбелердің беріліс функцияларына берілетін сыртқы әсер бейнесінің туындысы болып, ал бөлімі – ажыратылған жүйенің бірге үлкейтілген беріліс функциясы болып табылатын бөлгішке тең болады.

Ұқсас түрде басқа да сыртқы әсерлер үшін де өрнекті аламыз:

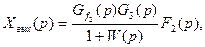(4.8)

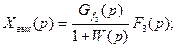(4.9)

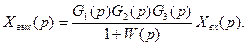(4.10)

Барлық әсерлердің бір уақытта әсер еткен кезіндегі тәтижелеуші X_шыг (p) мәні алынған мәндердің соммасы ретінде анықталады, ол келесі түрде жазылуы мүмкін:

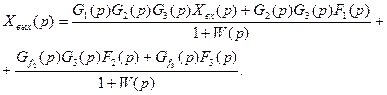(4.11)

(4.5) өрнегін қадағалау жүйесі үшін сипатты формулаларын (жеке жағдай сияқты) алуға болады. § 1.1 – де айтылғандай, соңғыларының ерекшелігі 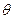_шыг шығыс шамасының салыстыру элементіне берілуі болып табылады, яғни жүйенің кірісіне бірге тең беріліс коэффициентімен. Одан бөлек, қадағалау жүйелеріндегі сыртқы әсерлердің негізгі түрі әдетте кейбір қатесі бар (келісіп) жүйемен өңделетін 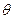_кір кіріс (басқарушы) әсер деп санайды. Θ = Θвх - Θвых .

Айтылғандарды ескере отырып, (4.6)–ға Z(p)=1–ді қойсақ, аламыз

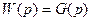(2.8)

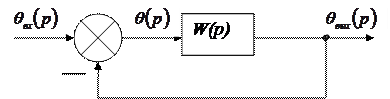
1.6. Сурет. Қадағалау жүйесінің құрылымдық схемасы

содан кейін (4.5)–гі кіріс пен шығыс шамаларды алмастырып аламыз

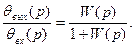(2.12)

Қадағалау жүйесінің сәйкес схемасы 2.6– суретте көрсетілген.

Лаплас түрлендірудің сызықтық күшінде, кіріс пен шығыс шамалардың операторлық қателесу бейнесі бір – бірімен оригиналы секілді байланысқан, яғни

Θ(р)= Θ_вх(р)- Θ_вых(р). (4.13)

(4.13)–тегі 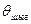(p) – ты анықтап алып, (4.12) – ге қойып шықсақ, күрделі емес түрлендіруден кейінгіні аламыз. 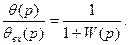(4.14)

(4.12) мен (4.14) өрнектері қадағалау жүйесінің шығыс шамасы мен қатесі бойынша сәйкес беріліс функциялары деп аталады.

Барлық қарастырылған жағдайлардағы тұйықталған басқару жүйесінің беріліс функциялары ажыратылған жүйенің беріліс функциясы W(p) арқылы анықталған. Соңғысы әдетте мына түрде берілуі мүмкін. 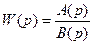(4.15)

мұндағы A(p), B(p) p – ден алынған полиномдар

(2.15) –ді (2.12) және (2.14) – не қойып шығып қадағалау жүйесінің есептеулері әшін пайдалы формулалар алуға болады:

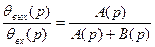(4.16)

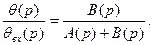(4.17)

Жоғарыда теріс таңбалы кері байланыс қарастырылған болатын. Оқушыларға жаттығулар ретінде мынаған көз жеткізуге болады, оң таңбалы кері байланыс жағдайында (2.5), (2.12), (2.14) формулалар алымындағы W(p) – ң алдындағы плюс таңбасы минусқа өзгеретінін көруге болады.

Мысал. Автоматты басқару жүйесінің құрылымдық схемасын (4.7, а сурет) түрлендіру және тұйықталған жүйенің беріліс функциясын жалпы түрде анықтау.

Құрылымдық схемасы қиылысқан параллель байланыстарға ие, осы түрлендіру бойынша беріліс функциясын құруға қолайлы түрге байланыстырады қайта қосу тәсілінің көмегімен түрлендіретін боламыз.

Z1 үзбесі арқылы W4 үзбесінің кірісіне келіп түсетін жергілікті кері байланысты W3 үзбесінің кірісіне ауыстырамыз. Нәтиже өзгермеуі үшін осы байланыс тізбегіне 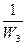тізбекті үзбе қосамыз. Z2 үзбесінің кірісіне W4 үзбесінің шығысынан берілетін бірге тең беріліс функциясы бар кері байланысты W5 үзбенің шығысынан беріліс функциясы бар кері байланысты W5 үзбесінің шығысынан 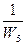беріліс функциялы байланысқа алмастырамыз.

1 және W2 беріліс функциялы параллельді келісіп қосылған үзбелерді бір үзбемен 1+W2 алмастырамыз. Осыдан кейін құрылымдық схема 4.7, б суретте көрсетілгендей түрге келеді.

Келесі қадам кері байланыс тізбегіндегі Z3 және 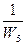екі параллель келісіп қосылған үзбелерді

Z₃ + 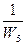беріліс функциялы эквивалентті үзбеге алмастыру болады. Енді бізде кері байланыстың екі параллель тізбегі бар (4.7, б. сурет) оларды мына беріліс функциялы эквивалентті үзбеге алмастыруға болады.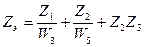

Жергілікті Z_э кері байланыспен қамтылған жүйенің тіке тізбегінің аймағын эквивалентті үзбемен алмастыра отырып, оның беріліс функциясы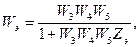

соңғы бір контурлы құрылымдық схеманы (2.13, г. сурет) аламыз, ажыратылған жүйенің беріліс функциясы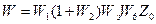

Тұйықталған жүйеніңберіліс функциясы

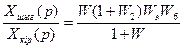
Соңғы өрнектің алдында алынған 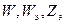мәндерін қойып шығып, соңғы өрнекті аламыз .

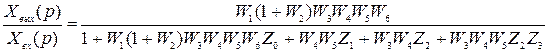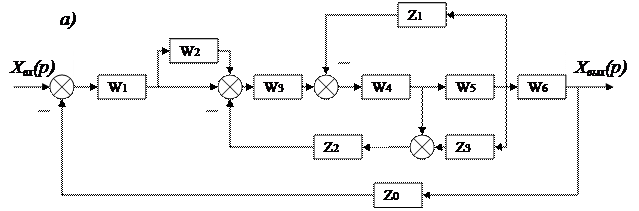
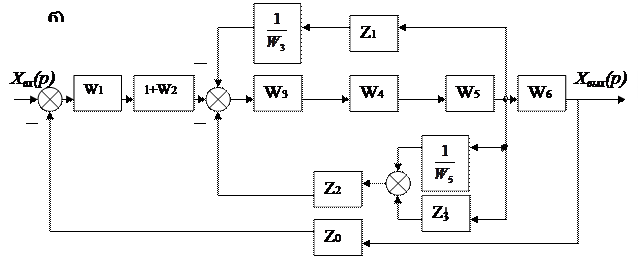
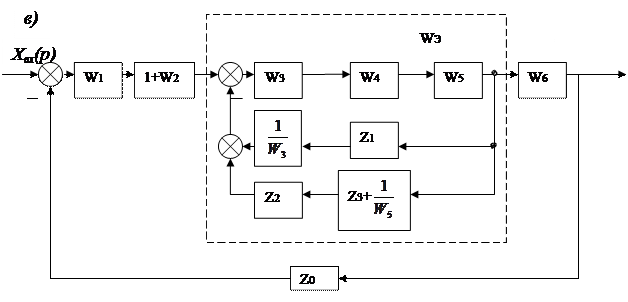
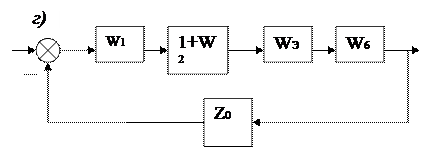
1.7. Сурет. Автоматты реттеу жүйесінің құрылымдық схемасының түрленуі

Негізгі әдебиет:1[106-123];

Қосымша әдебиет:1[129-137]; 2[31-39]

Бақылау сұрақтары:

1. Тізбектеп қосылған ТДБ анықтау және олардың БФ шығару.
2. Параллель-келісіп қосылған ТДБ анықтау және олардың БФ шығару.
3. Қарсы параллель қосылған ТДБ анықтау және олардың БФ шығару.
4. Методика получения операторного выражения системы, её характеристического уравнения.
5. Методика получения аналитических выражении ЧХ САУ (ВЧХ, МЧХ, АЧХ, ФЧХ, АФЧХ).

№ 5 Дәрістің конспектісі

Дәрістің тақырыбы: Сызықты жүйе төзімділігін зерттеу. (Сызықты жүйе төзімділігінің түсініктемесі мен жалпы шарты. Гурвиц және Раусс–тың алгебралық төзімділік критериялары. Михайлов пен Найквисттің жиіліктік тұрақтылық критериялары. Михайлов пен Найквисттің жиіліктік тұрақтылық критериясының жиіліктік жағдайлары. Вишнеградский критериясы, логарифмдік тұрақтылық критериясы. Тұрақтылық аймағын көрсету D – бөлу әдісі. Сипаттамалық басқару түбірлер мен оны тұрақтандырудың жүйе параметрлерінің әсері).

Автоматты реттеу жүйесі жұмысының процесінде жүйесі жұмысының процесінде әртүрлі қоздыру әсерлеріне душар болады, ол жүйені орнатылған режимінен, тең әсерлі күйден шығарып жібереді және реттелетін шаманы берілген мәннен келтіруге ұмтылады. Жүйе массасы, сиымдылық және басқада бар болуының салдарынан бір күйден басқа күйге лезде өтуі мүмкін. Қоздырушы әсер мен одан кейінгі жүйедегі реттегіштің қалпына келтіруші әсерлердің нәтижесінде өтпелі процестер пайда болады.

Осыдан үш түрлі процестер орын алады:

1. Реттелетін шама, ол қоздырушы әсер нәтижесінде берілген мәннен ауытқиды, реттегіштің әсерінен уақыт аралығында реттегіштің статикалық қателігіне жауап беретін дәлдікпен берілген мәнге қайта оралады. Мұндай өтпелі процесс үйлесімді деп, ал реттеу жүйесі – тұрақты деп аталады.

2. Реттелетін шама, қоздырушы әсердің нәтижесінде берілген мәннен ауытқыған, уақыт аралығында реттегіштің әсерінен ол мәнге жақындамай, берілген мәнге апериодты түрде немесе тербеліспен теориялы түрде шексіз оқшауланады, оның амплитудасы үздіксіз өседі. Мұндай өтпелі процесс тармақталған ал реттеу жүйесі – тұрақсыз деп аталады.

Шексіз өсетін амплитудан тербелу мүмкін болмаған сияқты қандай да бір физикалық параметрдің берілген мәннен шексіз ауытқуы болуы нақты жағдайда мүмкін емес екенін (айта кеткен) ескерген жөн.

Ауытқулар элементтердің қасиеттерімен шектеледі: электр машиналардың қанығуы, поршеньнің максималды жүрісі, қозғалтқыштың шектелген қуаты және т.бт дегенмен реттелетін шаманың бақыланбайтын ауытқуы немесе пайда болған тербелістер жабдықтардың бұзылмауы, қауіпсіздік және басқа түсініктемелер бойынша жіберілмейді.

3. Реттелетін шама, қоздыру әсерінен берілген мәннен ауытқыған, уақыт ішінде, реттегіш әсерінен орнатылған мәнге қайтып оралмай, бастапқы шартқа тәуелді амплитудамен өшпейтін тербеліс жасайды. Мұндай өтпелі процесс тербелістік, ал сызықты реттеу жүйесі – тұрақтылық шекарасында орналасқан деп аталады.

Бейсызықты жүйелерде амплитудасы тұрақты төзімді тербелісті тудыру мүмкін, оның шамасы кез – келген қоздырушы әсерді алғаннан кейін жүйе қайта оралатын бастапқы шартқа тәуелді. Мұндай жүйелерді орнықты тербелістер ретінде қарастырылады. (10. тарауды қара).

Орнықсыз автоматты реттеу жүйелері іс жүзінде жарамсыз болып табылады және сондықтан міндетті түрде жүйенің орнықтылығын (тұрақтылығын) зерттеу қажет.

Кез –келген статикалық жүйенің тепе – теңдігі орнықты ма екенін анықтау үшін осы жүйенің тепе – теңдік күйінен шамалы ауытқуы кезіндегі әрекетін білу қажет.

5.1. Сурет. Тепе – теңдіктің әртүрлі түрлері

Мысалы, шардың А күйіндегі тұрақтылығын (5.1. сурет) анықтау үшін оған кішкене ауытқу беріп, осы кезде пайда болған күшті қарастыру керек. Шардың А күйінен кез – келген шамалы ауытқуы кезде оны бастапқы күйге қайтып әкелетін күш пайда болады, және сәйкесінше бұл тепе – теңдік күйден шамалы ауытқыған кезде осы жағдайда тұрақсыз болып табылатын тепе – теңдік күйден ауытқуын жалғастыратын күштер пайда болады.

Көлденең жазықтықтағы С нүктесінде орналасқан шар бейтарап тепе – теңдікте орналасады, өйткені оның С нүктесінен ауытқыған кезде қосымша күштер пайда болмайды. D нүктесінде орналасқан шар жартылай тұрақты тепе – теңдікте орналасқан.

Шексіз аз ауытқулар кезіндегі жүйе орнықтылығын аз орнықты деп аталады. Көбінесе аз ғана тұрақты жүйелер соңғы жеткілікті .лкен ауытқуларда да тұрақты болып шығады, яғни жүйе үлкен орныққан болып табылады. Аз ғана орнықты, бірақ үлкен орнықсыз жүйелерді де кездестіруге болады.

5.1 –гі сурет. А нүктесінде орналасқан шар ауытқу В нүктесінде өткенге шейін тұрақтылығын жоғалтпайды. Жүйе аз ғана тұрақты, бірақ тек шектелген аймақта ғана жоғары орнықты.

Автоматты реттеу жүйелерді зерттеген кезде орнықтылығы (тұрақтылығы) аз жүйені қарастырады, яғни реттелетін шаманың орнатылған мәннен шамалы ауытқыған кездегі әрекетін.

Орнықтылығы аз сызықты жүйелерде үлкен орнықтылықты қамтамасыз етеді.

Бейсызықты жүйенің орнықтылығы аз, үлкен орнықсыз болып шығуы да мүмкін және сондықтан бейсызықты жүйенің орнықтылығын зерттеу әдістері.

Сызықты жіне сызықтандырылған жүйелерді қарастырамыз. Орыс ғалымы А.М. Ляпунов аз орнықтылықты сызықтандырылған теңдіктің көмегімен зерттеу есептің дәл шешімін беретінін көрсетті.

Тепе – теңдік күйден аз ңана ауытқумен алынған сызықты автоматты реттеу жүйесінің бос қозғалысы тұйықталған жүйенің дифференциалдық тейдеуімен жазылады (4–28).

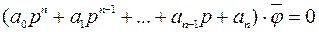(5.1)

Осындай теңдеумен бейнеленетін реттеу жүйесі, егер сипаттамалық теңдеудің барлық түбірлерінде нақты теріс бөлігі болған жағдайда ғана тұрақты болады.

Бұл тұжырымның дұрыс екенін келесі пікірлердің негізінде көз жеткізуге болады, (5.10) дифференциялдық теңдеуге сәйкес сипаттамалық теңдеулердің барлық түбірлері нақты және әртүрлі, мәндері p₁, p₂, p₃, …p_n деп жорамалдайық.

Сонда (5.1) теңдеудің шешімі мынадай болады:

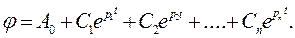(5.2)

Егер барлық түбірлері теріс болса, онда уақыт аралығында 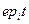көбейткішінен тұратын (5.2) өрнегінің барлық мүшелері нөльге ұмтылады, ал 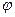реттелетін шаманың ауытқуы тұрақты А₀ мәнге немесе нөльге ұмтылады. Жүйе орнықты.

Егер түбірлердің ең болмағанда біреуі, мысалы p₁ оң болса, онда сәйкес С₁e^p₁^t мүшесі уақыт бойынша шексіз өседі және 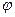реттелетін шамасының ауытқуы да өседі. Жүйе орнықсыз.

Комплексті түрде қосылған түбірлер теріс таңбалы нақты бөлігіндегі реттелетін шаманың ауытқуы өшіп қалған гармониялық тербеліспен орнатылған мәнге келеді. Жүйе орнықты.

Ең болмағанда түбірлердің бір жұбының нақты бөлігінің оң мәніндегі реттелетін шаманың ауытқуы амплитудасы шексіз өсстен тербеліс жасайды. Жүйе орнықсыз.

Егер сызықтандырылған жүйенің сипаттамалы теңдеуінде оң таңбалы түбірі болмай, ең болмағанда бір нөльдік түбірі немесе екі таза жорамал қосылған түбірлері бар болса, онда нақты жүйенің әрекеті оның сызықтандырылған теңдеуімен анықтала алмайды. Ондай жағдайда теңдеуді сызықтандыру кезде жойылған екі және жоғары туындысы бар мүшелері жүйенің орнықтылығына едәуір әсер етеді.