Идеальный проводник в электрическом поле

При помещении проводника в электрическое поле, свободные заряды приходят в движение. В результате на противоположных краях проводника возникают заряды противоположного знака (индуцированные заряды).

Поле индуцированных зарядов компенсирует внешнее поле и внутри поле равно нулю:

1) Заряды располагаются на поверхности.

2) Е _{внутреннее} = 0 (это используется для электростатической защиты.

3) Потенциал всего проводника одинаков и равно константе.

4) Напряженность поля у поверхности перпендикулярно к ней.

11. Электроёмкость уединенного проводника.

Конденсаторы.

Если проводнику сообщить заряды q₁, q₂, … q_n то его потенциал будет φ₁, φ₂, … φ_n. Из опыта следует что отношение C = q/φ для данного проводника остаётся постоянным, т.е. С=q₁/ φ₁, q₂/ φ₂, … q_n/ φ_n .

Величина равная 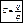— называется электроёмкостью (или электроемкостью проводника).

[C] = Кл/В = Ф (фарад)

В частности для шара радиусом R потенциал равен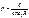

тогда ёмкость шара:

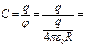
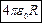— ёмкость шара

Если к заряженному проводнику провести другой, то на нём возникают индуцированные заряды, которые будут ослаблять электрическое поле первого проводника, т.е. уменьшать его потенциал и увеличивать его ёмкость.

Следовательно ёмкость двух проводников всегда больше емкости удельного проводника.

Для накопления больших зарядов служат

конденсаторы — системы из двух проводников разделенных диэлектриком.

Чтобы на ёмкость конденсатора не влияли окружающие проводники, всё поле должно быть сосредоточено внутри конденсатора.

Этому условию удовлетворяют: плоский, сферический и цилиндрический конденсаторы.

Ёмкость конденсатора равна: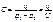

q — заряд одного из проводников.

U — разность потенциалов.

Электроемкость конденсаторов

Различной геометрической конфигурации.

Плоский конденсатор

Две параллельные пластины разделенные диэлектриком.

Напряженность внутри конденсатора: Е = G/ε₀

Разность потенциалов: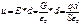

Следовательно: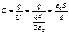

Если между пластинами нет вакуума,

а диэлектрик то: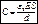

Сферический конденсатор

Две сферы заключенные одна в одну.

Разность потенциалов двух сфер: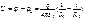

Ёмкость: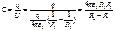

Цилиндрический конденсатор

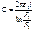
Соединение конденсаторов:

При параллельном соединении напряжение на параллельных конденсаторах одинаково (q₁= C₁*U; q₂= C₂*U; q₃= C₃*U) общий заряд: q_общ = q₁+ q₂+ q₃ = C₁U+C₂U+C₃U = (C₁+C₂+C₃)U.

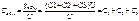
При параллельном соединении заряд на конденсаторах одинаков. Напряжение на конденсаторах: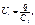

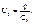
Общее напряжение: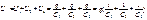

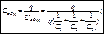
При параллельном соединении ёмкость складывается, а при последовательном вычитается.

Энергия заряженного конденсатора.