Динамика материальной точки и тела, движущегося поступательно 3 страница

Пример 13.Материальная точка массой m=10 г совершает гармонические колебания частотой n = 0,2 Гц. Амплитуда колебаний равна 5 см. Определить: а) максимальную силу, действующую на точку; б) полную энергию колеблющейся точки.

Решение. Уравнение гармонического колебания: х= A cos (ω₀t+ φ).

Тогда скорость и ускорение колеблющейся точки находятся так :

;

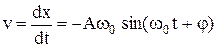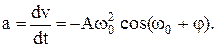
Согласно второму закону Ньютона сила, действующая на точку, –

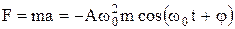при .

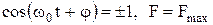Поэтому искомое максимальное значение силы (с учетом того, что ω₀= 2πn) будет равно

.

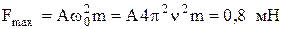Полная энергия колеблющейся точки –

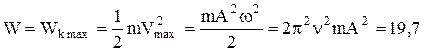мкДж.

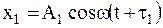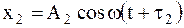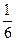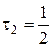Пример 14. Складываются два колебания одинакового направления, выражаемые уравнениями и , где А₁=1см, А₂=2см, τ₁= с, с, .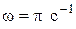

Определить начальные фазы φ₀₁, φ₀₂ составляющих колебаний и амплитуду результирующего колебания.

Решение. Уравнение гармонического колебания имеет вид

x = Acos(ωt+φ).

x₁=A₁cos(ωt+ωτ₁), x₂ =A₂cos(ωt+ ωτ₂).

Тогда:

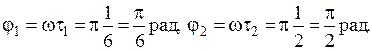
Для определения амплитуды результирующего колебания представим векторную диаграмму, см. рисунок.

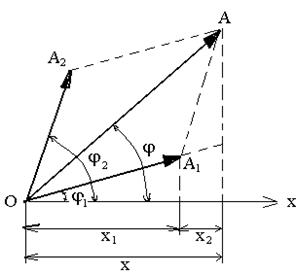
Согласно теореме косинусов, получим:

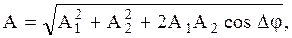
где 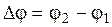– разность фаз составляющих колебаний.

Подставив найденные значения φ₂ и φ₁, получим, что 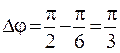(рад), 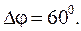Подставив значения А₁, А₂, и Δφ, найдем, что

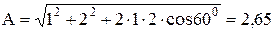см.

Пример 15.Точка участвует одновременно в двух гармонических колебаниях во взаимно перпендикулярных направлениях. Колебания описываются уравнениями x= cos πt и y = cos 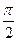t. Определить траекторию движения точки.

Решение. По условию задачи

x= cos πt ; y = cos 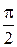t. (1)

Для определения траектории точки из выражений (1) исключаем понятие времени. Искомые уравнения имеют вид x= 2y²-1, или 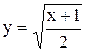, и представляют собой параболу.

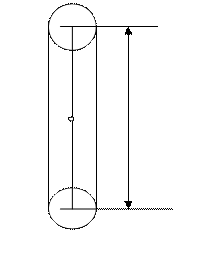
Пример 16.На концах тонкого стержня длиной 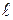=1 м и массой m=400 г укреплены шарики малых размеров массами m₁=200 г и m₂=300 г. Стержень колеблется вокруг горизонтальной оси, перпендикулярной ему и проходящей через его середину (точка О, см. рисунок). Определить период Т колебаний, совершаемых стержнем.

m₁ Решение. Период колебаний физического маятника,

примером которого является стержень с шариками,

определяется по формуле

О 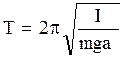, (1)

m₂

где I – момент инерции маятника относительно оси колебаний; m – его масса; a – расстояние от центра масс маятника до оси.

Момент инерции данного маятника равен сумме моментов инерции шариков I₁, I₂ и стержня I₃:

I= I₁+ I₂+ I_3. (2)

Приняв шарики за материальные точки, выразим моменты их инерций:

.

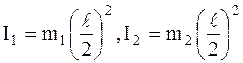Момент инерции стержня относительно оси, проходящей через его середину, равен I₃= 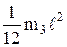. Подставив полученные выражения I₁, I₂, I₃ в формулу (2), найдем момент инерции физического маятника:

= .

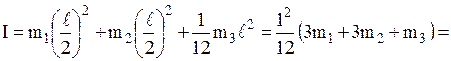
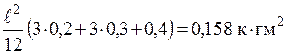Масса маятника состоит из масс шариков и стержня:

m = m₁ + m₂ + m₃ = 0,2 + 0,3 + 0,4 = 0,9 кг.

Если ось x направить вдоль стержня и начало координат совместить с точкой О, см. рисунок, то искомое расстояние «а» равно координате центра масс маятника, т.е.

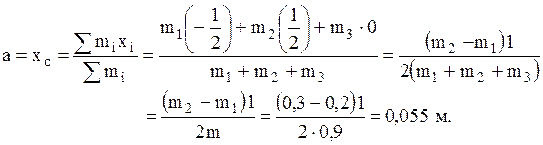
Произведя расчет по формуле (1), найдем период колебаний физического маятника:

.

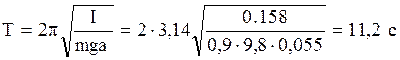Пример 17.Один конец медной проволоки длиной 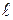=0,8 м, сечением 8 мм закреплен в подвесном устройстве, а к другому прикреплен груз массой m=400г. Вытянутую проволоку с грузом, отклонив до высоты подвеса, отпускают. Считая проволоку невесомой, определить ее удлинение в нижней точке траектории движения груза. Модуль Юнга для меди равен Е=118 ГПа.

Решение. Из закона Гука продольного растяжения

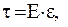
где 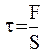– напряжение при упругой деформации; Е – модуль Юнга; 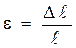– относительное продольное растяжение, получим

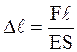, (1)

где F – сила, растягивающая проволоку в нижней точке траектории груза, численно равная сумме величин силы тяжести груза и центростремительной силы, действующей на него,

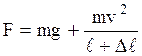, (2)

где v – скорость груза.

Согласно закону сохранения механической энергии

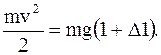
Подставив найденное отсюда выражение mv² в формулу (2), получим, что F=3mg. Тогда из выражения (1) следует, что искомое удлинение проволоки составляет

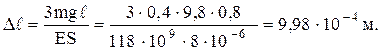
1.3. ЗАДАНИЯ

Вариант 1

1. Тело движется по прямой согласно уравнению S = 0,5t⁴ + 0,2t² +2. Найти скорость и ускорение тела в момент времени 4с. Каковы средние значения скорости и ускорения за первые 4 с движения ?

2. На токарном станке протачивается вал диаметром 60 мм. Скорость продольной подачи резца равна 0,5 мм за один оборот. Какова скорость резания, если за интервал времени 1 мин протачивается участок вала длиною 12 см?

3. Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами М. Одновременно на каждый из грузов кладут по перегрузку: справа – массой 3m; слева массой – m. Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы.

4. Тело брошено со скоростью 14 м/с под углом 30⁰ к горизонту. Найти нормальное и тангенциальное ускорение через 15 с после начала движения. Сопротивлением воздуха пренебречь.

5. Два небольших тела массой 2 кг и 1 кг связаны невесомой и нерастяжимой нитью и расположены на горизонтальной плоскости. К первому телу приложена сила 10 Н, направленная под углом 30⁰ к горизонту (вверх). Определить ускорение системы, если коэффициент трения тел о плоскость одинаков и равен 0,1.

6. Падающий вертикально шарик массой 0,2 кг ударился об пол и подпрыгнул на высоту 0,4 м. Найти среднюю силу, действующую со стороны пола на шарик, если длительность удара 0,01 с; к моменту удара об пол скорость шарика равна 5 м/с.

7. На полый тонкостенный цилиндр намотана нить, свободный конец которой прикреплен к потолку. Цилиндр сматывается с нити под действием собственного веса. Найти ускорение цилиндра и силу натяжения нити, если массой и толщиною нити можно пренебречь. Начальная длина нити намного больше радиуса цилиндра.

8. Кинетическая энергия вращающегося маховика равна 1000 Дж. Под действием постоянного тормозящего момента маховик начал вращаться равнозамедленно и, сделав 30 оборотов, остановился. Определить момент силы торможения.

9. Круглая платформа радиусом 1 м, момент инерции которой 130 кг×м², вращается по инерции вокруг вертикальной оси, делая 1 оборот в секунду. На краю платформы стоит человек, масса которого 60 кг. Сколько оборотов в секунду будет совершать платформа, если человек перейдет в ее центр? Момент инерции человека рассчитывать как для материальной точки.

10. К катящемуся шару массой 1 кг приложили силу в 1 Н, под действием которой шар остановился, пройдя путь 1 м. Определить скорость, с которой двигался шар до начала торможения.

11. Написать уравнение гармонических колебаний, совершающихся по закону косинуса. За время 1 мин совершается 60 колебаний, амплитуда которых 8 см, а начальная фаза равна 3/2p рад. Построить график зависимости смещения от времени.

12. Тонкий обруч радиусом 50 см подвешен на вбитый в стену гвоздь и колеблется в плоскости, параллельной стене. Найти период колебаний обруча.

13. Точка участвует в двух взаимно перпендикулярных колебаниях, выраженных уравнениями x=2cosωt и у=3sin0,5wt. Найти уравнение траектории точки и построить ее на чертеже.

14. Спираль обладает жесткостью К=25 Н/м. Определить массу тела, подвешенного к пружине, (тело за 1 мин совершает 25 колебаний).

15. Движение тела массой 2 кг описывается законом x=0,8sin(πt + π/₂). Определить энергию колеблющегося тела и максимальную силу, действующую на него.

Вариант 2

1. Уравнение движения материальной точки вдоль оси имеет вид x=A+Bt+Ct², где A=2 м; B=1 м/с; C=-0,5 м/с². Найти координату скорости и ускорения точки в момент времени t=2 с.

2. Колесо при вращении имеет начальную частоту 5 с^-1, после торможения его частота уменьшилась до 3 с^-1. Найти угловое ускорение колеса и число оборотов, сделанных им за это время.

3. Две гири массой 1 кг и 2 кг соединены невесомой нерастяжимой нитью, перекинутою через невесомый блок, подвешенный к динамометру. Какое значение покажет динамометр во время движения грузов? Трения в оси блока нет.

4. Пуля пробивает последовательно два вертикальных листа бумаги, расположенных на расстоянии 30 м друг от друга. При этом пробоина во втором листе находится на 2 мм ниже, чем в первом. С какой скоростью пуля подлетела к первому листу, если она подлетела к нему горизонтально?

5. Тело массой 990 г лежит на горизонтальной поверхности. В него попадает пуля массой 10 г и застревает в нем. Скорость пули равна 700 м/с и направлена горизонтально. Какой путь пройдет тело до остановки? Коэффициент трения между телом и поверхностью равен 0,05.

6. Камень массой 0,5 кг бросили под углом к горизонту с некоторой начальной скоростью. Его начальная кинетическая энергия равна 25 Дж. На высоте 2 м скорость камня равна v. Определить начальную скорость камня, скорость камня на высоте 2 м и угол, под которым бросили камень.

7. На сплошной цилиндрический вал радиусом 0,5 м намотан шнур, к концу которого привязан груз массой 10 кг. Найти момент инерции вала и его массу, если груз при разматывании шнура, опускается с ускорением 2 м/с².

8. Найти момент инерции тонкого стержня длиной 50 см и массой 0,36 кг относительно оси, перпендикулярной стержню и проходящей через: 1) конец стержня; 2) точку, отстоящую от стержня на 1/6 его длины.

9. Маховик в виде сплошного диска, момент инерции которого равен 150 кг×м², вращается с частотой 240 об/мин. Через минуту он остановился. Определить момент сил торможения, угловое ускорение, число оборотов маховика со времени начала торможения до полной остановки.

10. Полый тонкостенный цилиндр массой 500 г, катящийся без скольжения, ударяется о стенку и отскакивает от нее. Скорость цилиндра до удара о стенку равна 1,4 м/с, после удара 1 м/с. Определить выделившееся при ударе количество теплоты.

11. Уравнение движения материальной точки задано в виде x=2sin(π/₂t +π/₄) м. Определить период колебаний точки и максимальные значения ее скорости и ускорения.

12. Математический маятник, отведенный на натянутой нити на угол α от вертикали, проходит положение равновесия со скоростью v. Считая колебания гармоническими, найти частоту ω₀ собственных колебаний маятника.

13. Сигналы, подаваемые на горизонтальный и вертикальный входы осциллографа, определяются уравнениями x=Acos(wt+j), y=Acosωt. Найти траекторию движения для следующих случаев: а) j =0; б) j = 90⁰; в) j = 180⁰.

14. Вынужденные колебания описываются дифференциальным уравнениeм 0,1 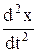+0,12 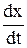+0,4x = 0,4sin1,5t. При какой частоте внешней силы будет наблюдаться резонанс?

15. Точка участвует одновременно в двух колебаниях одного направления, происходящих согласно уравнениям x₁=2sinωt и x₂=2sin(ωt+π/₂). Записать уравнение результирующего колебания и представить векторную диаграмму сложения амплитуд. Определить скорость и ускорение результирующего колебания.

Вариант 3.

1. Движение двух материальных точек выражаются следующими уравнениями: x₁=A₁+B₁t+C₁t², x₂=A₂+B₂t+C₂t² , где A₁=20 м; A₂ =2 м; B₂=B₁=2 м/с; C₁=-4м/с; C₂=0,5 м/c². В какой момент времени скорости этих точек будут одинаковыми? Определить скорости и ускорения точек в этот момент.

2. Диск радиусом 20 см вращается с угловым ускорением 3,14 рад/с². Найти для точек, находящихся на краю диска, к концу второй секунды после начала движения: а) угловую скорость; б) линейную скорость; в) тангенциальное, нормальное и полное ускорения.

3. Тело брошено с начальной скоростью 20 м/с под углом 60⁰ к горизонту. Найти радиус кривизны траектории в точке наивысшего подъема тела над поверхностью земли.

4. На наклонной плоскости укреплен блок, через который перекинута нить. К одному концу нити привязан груз массой 1 кг, лежащий на наклонной плоскости. На другом конце нити висит груз массой 3 кг. Наклонная плоскость образует с горизонтом угол в 30⁰. Коэффициент трения между грузом и наклонной плоскостью равен 0,1. Определить ускорение грузов.

5. Молекула летит со скоростью 500 м/с и упруго ударяется о поршень, движущийся навстречу ей. Скорость молекулы составляет угол в 60⁰ с нормалью поршня. Определить величину и направление скорости молекулы после удара. Скорость поршня равна 20 м/с.

6. Брусок скользящий по гладкой горизонтальной поверхности, со скоростью 5 м/с наезжает на шероховатую поверхность с коэффициентом трения, равным 0,8. При какой длине бруска его задняя грань остановится на границе гладкой и шероховатой поверхностей?

7. К ободу колеса, имеющему форму диска, радиус которого равен 0,5 м, а масса 50 кг, приложена касательная сила, равная 100 Н. Найти: а) угловое ускорение колеса; б) через какое время после начала действия силы колесо будет иметь частоту вращения 100 об/с.

8. На краю горизонтальной платформы, имеющей форму диска радиусом 2 м и массой 4 кг, стоит человек, масса которого равна 80 кг. Платформа может свободно вращаться вокруг вертикальной оси, проходящей через ее центр. С какой угловой скоростью будет вращаться платформа, если человек идет вдоль ее края со скоростью 2 м/с относительно платформы?

9. Определить момент инерции однородного диска радиусом 20 см и массой 1 кг относительно оси, перпендикулярной плоскости диска и проходящей через: а) центр диска; б) середину одного из радиусов диска.

10. Кинетическая энергия вала, вращающегося с постоянной частотой 6 об/с, равна 60 Дж. Найти момент импульса этого вала.

11. Материальная точка совершает гармонические колебания с частотой 0,5 Гц. Амплитуда колебания равна 3 см. Определить скорость точки в момент времени, когда смещение равно 1,5 см.

12. Как относятся длины математических маятников, если за одно и то же время один совершил 10, а другой 30 колебаний?

13. Однородный стержень совершает малые колебания в вертикальной плоскости вокруг горизонтальной оси, проходящей через его верхний конец. Длина стержня 0,5 м. Найти период колебаний стержня.

14. Дифференциальное уравнение колебаний математического маятника имеет вид 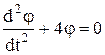. Определить период колебания маятника.

15. Складываются два гармоничеcких колебания одного направления, описываемые уравнениями x=3cos(2πt+π) см и x=3cos(2πt+π/₂) см. Записать уравнение результирующего колебания и представить векторную диаграмму сложения амплитуд. Построить график колебаний x₁, x₂ и результирующего колебания.

Вариант 4

1. Материальная точка массой 0,05 кг совершает гармонические колебания, уравнение которых имеет вид х=0,1sin5t. Найти силу, действующую на точку: а) в момент, когда фаза колебаний j=30⁰; б) при наибольшем отклонении точки.

2. Диск радиусом r = 20 см вращается согласно уравнению j = A +Bt+Ct³ , где A=3 рад; B= – 1 рад/с; C=0,1 рад/с³. Определить тангенциальное, нормальное и полное ускорения точек на окружности диска для момента времени, равного 10 с.

3. Снаряд, выпущенный из орудия под углом 30⁰ к горизонту, дважды был на одной и той же высоте h: спустя 10 с и 50 с после выстрела. Определить начальную скорость и высоту h.

4. Через вращающийся вокруг горизонтальной оси блок перекинута невесомая нерастяжимая нить, к концам которой привязаны грузы массой 0,5 кг и 0,6 кг. Найти силу давления блока на ось при движении грузов. Массой блока и трением в оси можно пренебречь.

5. Снаряд, летевший горизонтально со скоростью 100 м/с, разрывается на две равные части на высоте 40 м. Одна часть падает через 1 с на землю точно под местом взрыва. Определить величину и направление скорости движения второй части снаряда сразу после взрыва.

6. Тело, брошенное с высоты 5 м вертикально вниз со скоростью 20 м/с, погрузилось в грунт на глубину 20 см. Найти работу силы сопротивления грунта, если масса тела равна 2 кг. Сопротивлением воздуха пренебречь.

7. Маховое колесо, имеющее момент инерции 245 кг×м², вращается, делая 20 оборотов в секунду. Через 1 мин после того как на колесо перестал действовать вращающий момент, оно остановилось. Найти: а) момент сил трения; б) число оборотов, которое сделало колесо до полной остановки (после прекращения действия сил).

8. Летчик давит на сиденье кресла самолета в нижней точке петли Нестерова с силой в 7200 Н. Масса летчика 80 кг, радиус петли 250 м. Определить скорость самолета.

9. Платформа в виде диска вращается по инерции вокруг вертикальной оси с частотой 15 об/мин. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота возросла до 25 об/мин. Масса человека 70 кг. Определить массу платформы. Момент инерции человека рассчитывать как для материальной точки.

10. К ободу покоящегося диска массой 5 кг приложена постоянная касательная сила в 20 Н. Какую кинетическую энергию будет иметь диск через 5 с после начала действия силы? Диск может свободно вращаться относительно оси, проходящей через центр диска и перпендикулярной его плоскости.

11. Полная энергия тела, совершающего гармонические колебания по синусоидальному закону, равна 30 мкДж; максимальная сила, действующая на тело, составляет 1,5 мН. Написать закон движения этого тела, если период колебания равен 2 с и начальная фаза равна π/₃.

12. Определить период колебаний груза массой 2,5 кг, подвешенного к пружине, если пружина под действием силы в 30 Н растягивается на 9 см.

13. Точка одновременно участвует в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x=3cosωt и x=4cosωt. Определить уравнение траектории точки.

14. К пружине подвешен груз. Максимальная кинетическая энергия колебаний груза 1 Дж. Амплитуда колебаний равна 5 см. Найти жесткость пружины.

15. Два гармонических колебания одного направления, описываются такими уравнениями: x₁=2sin(2πt+π/₄) и x₂ =2sin(2πt+ 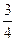π). Записать уравнение результирующего колебания и представить векторную диаграмму сложения амплитуд. Построить графики колебаний x₁, x₂ и результирующего колебания.

Вариант 5

1. Точка движется по прямой согласно уравнению S=6t+1/8t ³ (длина в метрах, время в секундах). Определить среднюю скорость и ускорение точки за интервал времени от 2 с до 6 с.

2. Тело вращается вокруг неподвижной оси по закону j=A+Bt+Ct², где A = 10 рад; В = 20 рад/c; С = -2 рад/с². Найти полное ускорение точки, находящейся на расстоянии 0,1 м от оси вращения, для момента времени, рав-ного 4 с.

3. В вагоне, движущемся горизонтально с ускорением 2 м/с², на шнуре висит груз массой 200 г. Найти силу натяжения шнура и угол его отклонения от вертикального положения.

4. Найти работу подъема груза по наклонной плоскости, если масса груза 100 кг, длина наклонной плоскости 2 м, угол наклона 30⁰, коэффициент трения 0,1, а груз движется с ускорением 1 м/с².

5. Два конькобежца массами 80 и 50 кг, держась за концы натянутого длинного шнура, неподвижно стоят на льду один против другого. Один из них начинает укорачивать шнур, выбирая его со скоростью 1 м/с. С какими скоростями будут двигаться по льду конькобежцы? Трением пренебречь.

6. Тело массой 10 кг брошено с высоты 100 м вертикально вниз со скоростью 14 м/с. Определить среднюю силу сопротивления грунта, если тело углубилось в него на 0,2 м. Сопротивление воздуха не учитывать.

7. Два маленьких шарика одинаковой массы (10 г) соединены стержнем, длина которого равна 20 см, а масса ничтожно мала. Определить момент инерции системы относительно оси, перпендикулярной стержню и проходящей через центр масс системы.

8. Через неподвижный блок перекинута нить, к концам которой привязаны грузы массой 100 г и 110 г. С каким ускорением они будут двигаться, если масса блока равна 400 г? Трением в блоке пренебречь.

9. Диск массой 2 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Найти кинетическую энергию диска.

10. Платформа в виде диска радиусом 1 м и массой 200 кг вращается вокруг вертикальной оси, делая 1 оборот в минуту. На краю нее стоит человек массой 50 кг. Сколько оборотов в секунду будет делать платформа, если человек перейдет на полметра ближе к центру. Считать платформу однородным диском, а человека – точечной массой.

11. Точка совершает гармонические колебания с частотой 10 Гц. В момент, принятый за начальный, точка имела максимальное смещение 1 мм. Написать уравнение колебаний точки и начертить их график.

12. Скорость материальной точки, совершающей гармонические колебания, задается уравнением V(t)=–6sin2πt. Записать зависимость смещения этой точки от времени.

13. Найти отношение длин двух математических маятников, если отношение периодов их колебаний равно 1,5.

14. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x=3cos2ωt см и y=4cos(2ωt +π) см. Записать уравнение траектории движения точки и построить график колебания.

15. Точка совершает одновременно два гармонических колебания, происходящих вдоль оси x и описываемых уравнениями x₁ = 3 cos (ωt + π/4) см и x₂ = cos (ωt - 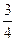π) см. Записать уравнение результирующего колебания и представить векторную диаграмму сложения амплитуд. Найти максимальную скорость колебания, построить графики колебаний x₁ и x₂ и скорости результирующего колебания.

Вариант 6

1. Уравнения прямолинейного движения точек заданы в виде S₁ = 4t² + t и S₂ = 5t³ + t² (расстояние – в метрах, время – в секундах). В какой момент времени скорости точек будут равны? Определить ускорение в этот момент времени.

2. Угол поворота диска радиусом 10 см изменяется со временем по закону j=4+2t-t³. Определить угловую скорость, угловое ускорение и линейную скорость на ободе диска в момент времени, равный 0,5 с.

3. Тело брошено со скоростью 10 м/с под углом 45⁰ к горизонту. Найти радиусы кривизны траектории тела спустя 0,5 с после начала движения и в точке наивысшего подъема тела над поверхностью земли.

4. Определить работу, совершаемую при подъеме груза массой 50 кг по наклонной плоскости с углом наклона 30⁰ к горизонту на высоту 4 м, если время подъема – 2 с, а коэффициент трения равен 0,06.

5. Из пушки, стоящей на гладкой горизонтальной площадке, стреляют под углом 30⁰ к горизонту. Масса снаряда 20 кг, его начальная скорость 200 м/с. Какую скорость приобретет пушка при выстреле, если ее масса 500 кг?

6. Брошенное вертикально вверх тело массой 200 г упало на землю спустя 1,44 с. Найти кинетическую энергию тела в момент падения на землю и потенциальную энергию в верхней точке траектории.

7. На краю горизонтально вращающейся платформы радиусом 1 м лежит груз. В какой момент времени после начала вращения платформы груз соскользнет с нее, если ее вращение – равноускоренное, а в момент времени, равный 2 мин, она имеет угловую скорость 1,4 рад/с? Коэффициент трения между грузом и платформой равен 0,05

8. Диск массой 0,6 кг и диаметром 40 см вращается с угловой скоростью 157 рад/с. При торможении он останавливается в течение 10 с. Найти среднюю величину тормозящего момента.

9. Прыгун в воду может уменьшить свой момент инерции примерно в 3,5 раза, если согнется. Если в согнутом состоянии он совершает 2 оборота за 15 с, какова его угловая скорость, когда он находится в распрямленном состоянии?

10. Обруч и диск имеют одинаковую массу и катятся без проскальзывания с одинаковой скоростью. Кинетическая энергия обруча равна 40 Дж. Найти кинетическую энергию диска.

11. Период гармонических колебаний составляет 4 с. Определить время t₁, за которое тело, совершающее эти колебания, пройдет путь, равный половине амплитуды, если в начальный момент времени тело проходило положение равновесия; s₂ – путь, равный амплитуде; s₃ – путь, равный 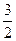амплитуды.

12. Полная энергия гармонически колеблющейся точки равна 10 мк×Дж, а максимальная сила, действующая на точку, равна 0,5 мН. Написать уравнение движения этой точки, если период колебаний составляет 4 с, а начальная фаза π/6.