Изучение колебаний связанных маятников

Цель лабораторной работы

Изучение гармонических (нормальных) колебаний связанной системы двух маятников. Изучение биений как результата сложения нормальных колебаний связанной системы двух маятников.

Экспериментальное оборудование, приборы ипринадлежности

Лабораторная установка показана на рис. 1.

Рис. 1

На основании 1 установлен вертикальный стенд 2 с системой подвеса маятников 3 и 4, которые соединены пружинами 5, 6. Пружины закрепляются на фиксаторах, которые свободно перемещаются по резьбе верхних и нижних стержней маятников. Частота свободных колебаний маятников регулируется перемещением грузов 7. Начальные условия колебания маятников задаются с помощью секторов, размещенных на штанге стартового устройства 11. Сектора 9. 10 служат для запуска антифазных колебаний. Сектора стартового

устройства приводится в движение поворотом штанги одной из рукояток 12. На маятниках укреплены датчики угловой скорости 13, 14. Передача данных в компьютер осуществляется с помощью двух USB-кабелей 15 и 16.

К приборам и принадлежностям относится компьютер с программным обеспечением для регистрации и обработки данных.

Теоретическая часть

3.1. Связанная колебательная система.

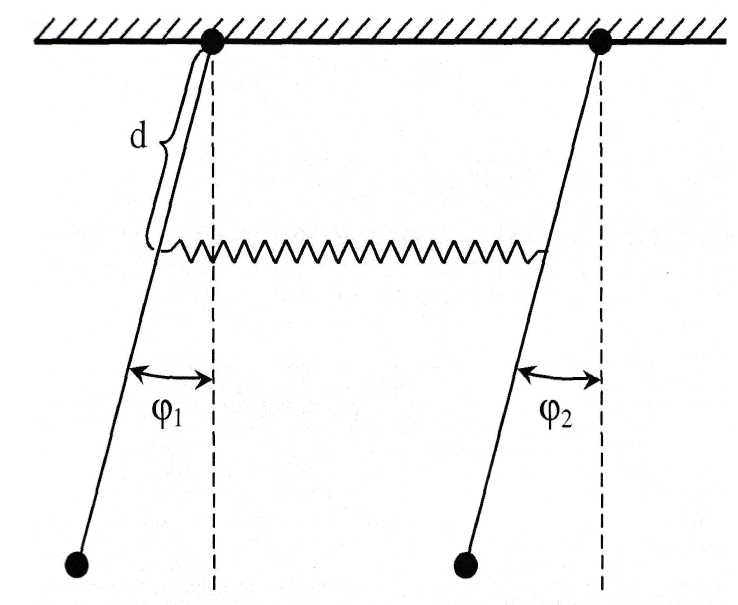
Рис. 2.

Связанная колебательная система- это совокупность двух или нескольких маятников (парциальных систем),каким-либо образом связанных между собой. В качестве примера рассмотрим систему, изображенную на рис. 2. Она состоит из двух математических маятников массой т и длиной l, связанных невесомой пружиной с коэффициентом жесткости k. При движении маятников в одной вертикальной плоскости состояние такой системы полностью описывается двумя независимыми параметрами - углами φ₁иφ₂отклонения маятников от вертикали, т.е. система имеет две степени свободы.

Уравнение движения для каждого маятника можно получить из общего уравнения динамики вращательного движения вокруг неподвижной оси:

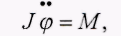(1)

где J - момент инерции тела относительно оси вращения; М - момент действующих на тело сил относительно той же оси.

Применительно к каждому маятнику уравнение (1) для малых колебаний имеет вид:

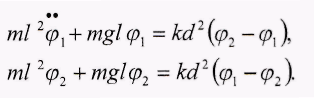
(2)

Здесь учтено, что при малых φ₁и φ₂удлинение пружины равно d(φ₁- φ₂)и, следовательно, момент М упругой силы равен kd²(φ₁- φ₂), поскольку плечо этой силы равно d. Предполагается, что момент сил трения, действующих на маятники, много меньше Ми затуханием можно пренебречь. Общее решение системы (2) имеет вид

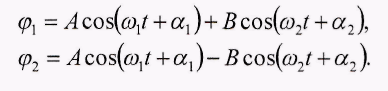(3)

где постоянные А, В, α₁и α₂определяются из начальных условий, а частоты ω₁.,ω₂.даются формулами:

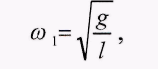
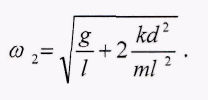(4)

Из соотношений (3) следует, что в общем случае каждый маятник осуществляет сложное колебание, которое не является гармоническим, поскольку складывается из двух независимых колебаний с частотами ω₁.иω₂

Нормальные колебания

Специальным подбором начальных условий можно добиться возбуждения колебаний системы только с одной частотой. Такие колебания, при которых оба маятника колеблются с одной и той же частотой, называются нормальными колебаниями. Частоты таких колебаний называются нормальными частотами. Число нормальных колебаний равно числу степеней свободы системы.

В рассматриваемом случае двух связанных маятников нормальные колебания могут быть возбуждены следующими двумя способами.

Синфазные колебания- это колебания маятников, происходящие в одной фазе с меньшей из нормальных частот ω₁. Они описываются выражениями (3) при В = 0, что соответствует начальным условиям

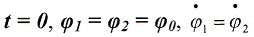(5)

Это означает, что в начальный момент времени оба маятника отклонены на один и тот же угол и имеют одинаковые скорости (например, нулевые). Роль связи при таких колебаниях исчезает.

Антифазные колебания- это колебания маятников, происходящие в противофазе с большей из нормальных частот ω₂. Они описываются соотношениями (3) при А = 0, что приводит к начальным условиям

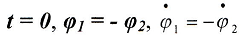(6)

Отсюда следует, что в начальный момент времени маятники отклоняются на противоположный угол и имеют противоположные угловые скорости.

В общем случае произвольных начальных условий будут одновременно совершаться оба нормальных колебания. При этом возникают биения -периодическое возрастание и убывание амплитуды колебаний каждого из маятников.

Биения удобно наблюдать при начальных условиях

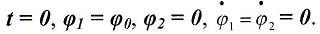(7)

При этом постоянные системы (3) имеют значения

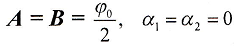(8)

После подстановки выражений (8) в уравнения (3) получим

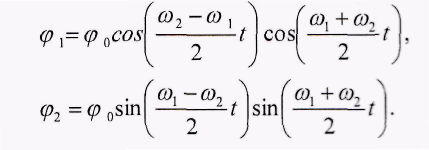(9)

Предположим, что связь между маятниками является слабой, т.е.

ω₂- ω ₁<<ω₁а значит, как следует из соотношений (4).

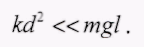(10)

Из уравнений (9) вытекает, что в этом случае движение маятников можно считать колебаниями, происходящими с

частотой 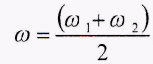, и амплитудами, медленно меняющимися во времени. Период этих медленных изменений амплитуд определяется выражением

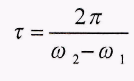(11)

и называется периодом биений. При этом фазы колебаний маятников отличаются на π/2. Уменьшение амплитуды одного из маятников приводит к увеличению амплитуды второго. Общая энергия системы (без учета потерь) остается постоянной, но «перекачивается» от одного маятника к другому.

Отметим, что если связанная система состоит из трех парциальных систем например, трех математических маятников, соединенных пружинами, она обладает тремя системами свободы и тремя нормальными частотами. Если же число парциальных систем равно n, то связанная система обладает n степенями свободы и имеет n нормальных частот.

Явление резонанса.

Для получения незатухающих (вынужденных) колебаний на систему воздействуют периодической внешней силой. Тогда всякий раз, когда частота внешнего воздействия ω становится равной нормальной частоте ω₁ или ω₂ наступает резонанс. Резонанс - явление резкого возрастания амплитуды колебаний при приближении частоты внешнего воздействия к собственной (нормальной) частоте колебательной системы.

Когда частота внешнего воздействия равна одной из мод, оба маятника движутся так, как если бы их колебания принадлежали этой моде (при свободных колебаниях). Так, при ω= ω₁будем наблюдать синфазные колебания (моду 1), а при ω = ω₂- антифазные колебания (моду 2). Таким образом, резонансная кривая системы двух связанных маятников имеет два максимума.