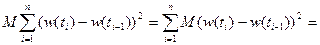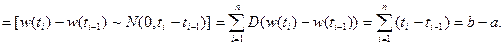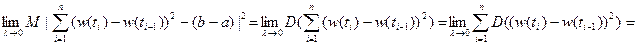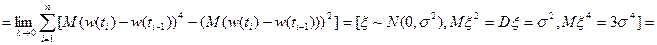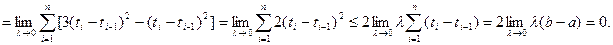Броуновское движение. Винеровский процесс

Винеровский процесс, или процесс броуновского движения, имел большое значение при разработке теории случайных процессов. Многие распределения, используемые в теории управления, можно моделировать процессами, порождаемыми винеровскими процессами.

В 1827 г. английский ботаник Р. Броун заметил, что маленькие частицы диаметром около микрона, погруженные в жидкость, находятся в постоянном хаотическом движении. В 1905 г. А. Эйнштейн объяснил это движение как результат столкновения частиц с молекулами жидкости. Он разработал математическую модель броуновского движения. Строгий математический анализ броуновского движения дал Н. Винер в 1923 г.

Рассмотрим движение частицы на координатной прямой. Зафиксируем координату x броуновской частицы на числовой прямой и будем считать, что изменение положения частицы происходит в моменты времени, кратные 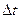, влево и вправо на 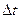с равной вероятностью.

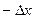
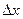
x

Пусть случайный процесс 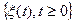задаёт положение частицы в момент времени 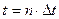. Предположим, что

1) .

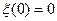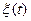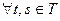
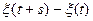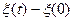2) -- процесс с независимыми приращениями, т.е. и -- независимые случайные величины.

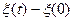
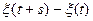
0 t t+s

3) Приращения на промежутках одинаковой длины 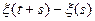и 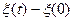одинаково распределены.

Т.к. отдельное смещение мало (за время 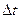), естественно считать, что положение частицы в момент времени t определяется как сумма малых смещений, к которой применима центральная предельная теорема.

Определение. Броуновским движением называется случайный процесс 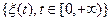, для которого выполняются следующие условия:

1) ;

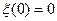2) 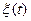-- процесс с независимыми приращениями;

3) приращения 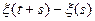имеет нормальное распределение с параметрами 0 и 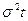, т.е. .

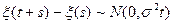В силу независимости приращений 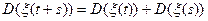, тогда , .

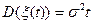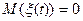Если 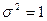, то броуновское движение называется винеровским процессом и обозначается 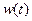или .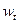

Определение. Винеровским процессом 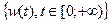называется процесс, для которого:

1. ;
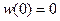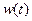2. -- процесс с независимыми приращениями;
3. .

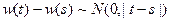Обозначим через ,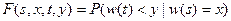

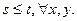
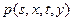-- переходная плотность винеровского процесса:

.

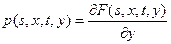Найдем функцию :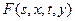

.

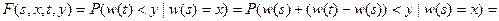
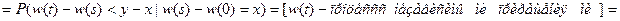
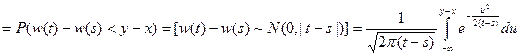Тогда переходная плотность .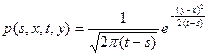

Можно показать, что эта плотность удовлетворяет уравнению Фоккера-Планка-Колмогорова:

.

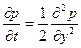Некоторые свойства Винеровского процесса:

1. У Винеровского процесса существует модификация с непрерывными траекториями (с вероятностью 1 траектории Винеровского процесса являются непрерывными).

2. С вероятностью 1 траектории Винеровского процесса не имеют производные ни в одной точке.

3. С вероятностью 1 траектории Винеровского процесса имеют неограниченную вариацию на любом конечном интервале.

4. Сумма квадратов приращений Винеровского процесса, соответствующих их разбиению на 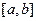, сходится к длине этого отрезка в среднем квадратическом смысле при мелкости разбиения, стремящейся к нулю, т.е.

,

.

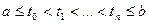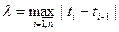
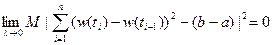Доказательство. Рассмотрим