Функции индивидуального спроса.
Потребителя.
4.1. Постройте бюджетные ограничения и запишите их уравнения, если:
а) Семья тратит на фрукты 30рублей, приобретая только яблоки и бананы. Цена яблок 3 рубля, цена бананов 6рублей. Что произойдет при изменении цен и суммы, запланированной на расходы?
б) Продовольственные талоны выдаются на сумму F, I – доход, p – средняя цена единицы продовольственных товаров, х – количество потребляемого продовольствия.
в) Авиакомпания предоставляет премию постоянному клиенту. Пусть I – доход клиента, p – цена 1000км перелета, Qm – минимальное расстояние, за которое предоставляется премия, Q0 – величина натуральной премии. (Подсказка: считать, что премия может быть предоставлена только 1 раз; рассмотрите случаи, когда доход клиента больше или меньше суммы, необходимой для осуществления перелета на расстояние Qm)
г) Бедным семьям предоставляется частичная скидка на оплату жилья. Размер льготной жилой площади 50 кв. метров, pS – субсидируемая цена за квадратный метр, pM – рыночная цена за квадратный метр, I – доход семьи в месяц.
4.2. Нарисуйте кривые безразличия и определите функции полезности:
а) Дошкольника Васи, который абсолютно равнодушен к овсяной каше (x) и всегда норовит отдать ее сестре, но зато готов съесть сколько угодно картофельных оладий (y).
б) Домохозяйки Марии, которая терпеть не может тараканов; испорченное настроение от каждого замеченного таракана (x) может быть поправлено только при помощи шоколадной конфеты (y).
в) Студента Валерия, считающего, что 1 гамбургер (x) прекрасно заменяют 2 пирожка с капустой (y).
г) Пенсионерки Матильды Петровны, которая по утрам пьет чай (x) исключительно с молоком (y), причем в равных пропорциях.
д) Мистера Бонда, который круглосуточно предпочитает «очень сухой мартини»: 2 части джина (x) на 1 часть вермута (y).
е) Сторонница раздельного питания Оксаны, которая употребляет либо мясо (x), либо рыбу (y), но не любит их смешивать – старается не употреблять мясные, и рыбные продукты в течение одного дня.
4.3. Определите MRSxy и нарисуйте кривые безразличия для функций полезности:
а) 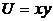 ,
, 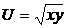 ,
,  ;
;
б) 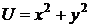 ,
, 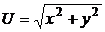 ;
;
в) 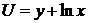 ,
, 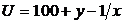 ;
;
г) 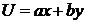 с различными коэффициентами
с различными коэффициентами 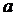 и
и 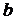 .
.
4.4. Как изменится бюджетное ограничение (в случае 2-х товаров), если на первый товар накладывается количественный (потоварный) налог t, на второй - потоварная субсидия w, и потребитель платит паушальный (подоходный) налог T? Покажите изменения графически.
4.5.
Тема 5. Оптимальный выбор потребителя.
Тема 6. Сравнительная статика спроса.
Эффекты дохода и замещения.
3.
4.
5.
6.
6.1. Функция полезности потребителя 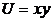 . Первоначальное бюджетное ограничение
. Первоначальное бюджетное ограничение 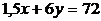 . В результате снижения цены Ру, бюджетное ограничение приобрело вид:
. В результате снижения цены Ру, бюджетное ограничение приобрело вид: 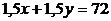 . Найдите эффекты дохода и замещения на товары для декомпозиции изменения спроса по Хиксу и Слуцкому.
. Найдите эффекты дохода и замещения на товары для декомпозиции изменения спроса по Хиксу и Слуцкому.
6.2. Функция полезности потребителя 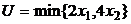 . Известны цены и доход:
. Известны цены и доход: 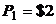 ,
, 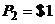 ,
, 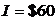 . Цена на первое благо повышается до
. Цена на первое благо повышается до 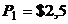 . Найдите эффекты дохода и замещения по Хиксу и Слуцкому.
. Найдите эффекты дохода и замещения по Хиксу и Слуцкому.
6.3. Известна функция полезности потребителя 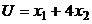 . Первоначальное бюджетное ограничение
. Первоначальное бюджетное ограничение 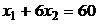 . В результате роста цен бюджетное ограничение приняло вид:
. В результате роста цен бюджетное ограничение приняло вид: 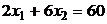 . Найдите эффекты дохода и замещения по Хиксу и Слуцкому.
. Найдите эффекты дохода и замещения по Хиксу и Слуцкому.
6.4. Покажите графически эффекты дохода и замещения по Хиксу и Слуцкому при понижении цены товара x, если:
а) x – нормальное благо;
б) x – инфериорное благо;
в) x –благо Гиффена.
6.5. Покажите графически эффекты дохода и замещения по Хиксу и Слуцкому при повышении цены товара y, если:
а) y – нормальное благо;
б) y– инфериорное благо;
в) y –благо Гиффена.
6.6. Потребитель имеет функцию полезности U = xy + z.
а) Найдите спрос на каждый товар. (Известно, что доход 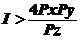 .)
.)
б) Используя уравнение Слуцкого, определите перекрестный эффект замещения для товара x при изменении цены товара y.
в) Как функция спроса на z может быть использована для оценки выгоды от снижения цены Pz ?
6.7. Доли расходов на три товара равны соответственно 20%, 50% и 30%. Известно, что эластичность спроса по доходу на первое благо равна (–1), а на второе благо равна 2. Определите эластичность спроса по доходу на третье благо.
6.8. Когда[2] цена товара х возрастает на 1%, то величина спроса на него сокращается на 2%. Эластичность спроса по доходу на товар х равна 0.5. Доля товара х в общих расходах потребителя: 10%. Определите:
а) эластичность компенсированного спроса на товар х;
б) верно ли, что компенсированный спрос всегда менее эластичен, чем некомпенсированный?
6.9. Пусть потребитель покупает 2 товара: x и y. Доля расходов на y равна 0.8. Эластичность спроса на y по доходу: 1.05. Перекрестная эластичность спроса на у по цене товара х равна 0.5. Определите:
а) эластичность некомпенсированного спроса на х по своей цене( 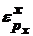 );
);
б) эластичность компенсированного спроса на товар х по своей цене ( 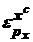 );
);
в) перекрестную эластичность замещения для товара y по цене pX ( 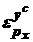 );
);
г) верно ли, что товары x и y являются общими субститутами, но чистыми комплементами?
6.10. Охарактеризуйте2 товары x и y, если при изменении цены товара y перекрестный эффект дохода действует в направлении, противоположном перекрестному эффекту замещения и превышает его по абсолютной величине.
6.11. Охарактеризуйте2 товары x и y, если при изменении цены товара y перекрестный эффект дохода действует в том же направлении, что и перекрестный эффект замещения и превышает его по абсолютной величине.
Индексы стоимости жизни.
5.
6.
7.
8.
8.1. Результаты двух наблюдений за поведением потребителей A и B:
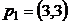 ,
, 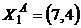 ,
, 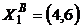 ,
,
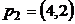 ,
, 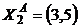 ,
, 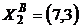 ,
,
где 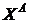 ,
, 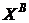 – наборы товаров, предпочитаемых потребителями,
– наборы товаров, предпочитаемых потребителями, 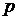 – вектор цен. Удовлетворяет ли требованиям слабой (сильной) аксиомы выявленных предпочтений поведение: а) потребителя A; б) потребителя B; в) семьи (A +B)?
– вектор цен. Удовлетворяет ли требованиям слабой (сильной) аксиомы выявленных предпочтений поведение: а) потребителя A; б) потребителя B; в) семьи (A +B)?
8.2. Результаты трех наблюдений за потребителем:
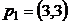 ,
, 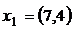 ,
,
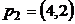 ,
, 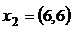 ,
,
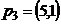 ,
, 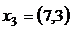 ,
,
где 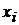 – набор товаров для
– набор товаров для 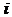 ситуации,
ситуации, 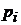 – вектор цен. Удовлетворяет ли такое поведение требованиям слабой (сильной) аксиомы выявленных предпочтений?
– вектор цен. Удовлетворяет ли такое поведение требованиям слабой (сильной) аксиомы выявленных предпочтений?
8.3. Максимизирует ли потребитель полезность в следующих случаях:
а) 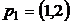 ,
, 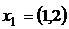 ,в)
,в) 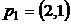 ,
, 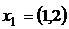 ,
,
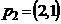 ,
, 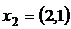 ;
; 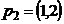 ,
, 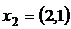 ;
;
б) 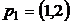 ,
, 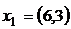 ,г)
,г) 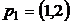 ,
, 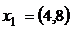 ,
,
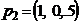 ,
, 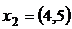 ;
; 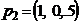 ,
, 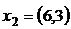 ;
;
где 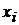 – набор товаров для
– набор товаров для 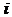 ситуации,
ситуации, 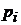 - вектор цен.
- вектор цен.
8.4. Результаты наблюдений поведения потребителя:
| х1 | х2 | х3 | р1 | р2 | р3 | |
| Ситуация 1 | ||||||
| Ситуация 2 | ||||||
| Ситуация 3 |
где (х1, х2, х3) - набор товаров в i-й ситуации, (р1, р2, р3) - вектор цен. Рационально ли поведение потребителя?
8.5. Совершено ограбление поезда. Из показаний официанта полиция знает некоторые особенности потребления преступника:
| Пиво | Сосиски | |||
| х1 | р1 | х2 | р2 | |
| Преступник |
В совершении преступления подозреваются граждане А, В и С. Можно ли определить, кто преступник, по следующим наблюдениям?
| Пиво | Сосиски | |||
| х1 | р1 | х2 | р2 | |
| А | ||||
| В | ||||
| С | 1,5 |
8.6. Определите:
а) На сколько вырастут индексы цен Пааше и Ласпейреса, если цены в 2006 году увеличатся на 20 % по сравнению с 2005 годом?
б)На сколько вырастают количественные индексы Пааше и Ласпейреса, если цены в 1996 году увеличились на 100 % по сравнению с 1994 годом. Известно, что общие расходы каждого потребителя выросли на 200 %?.
8.7. Москвичка Лариса тратит 100рублей ежемесячно на мороженое и конфеты. В Москве она покупает 10порций мороженого по 4рубля и 3кг конфет по 20рублей за 1 кг. Лето Лариса проводит у бабушки в Нижнем Новгороде, где конфеты стоят 25руб., а мороженое 2,5 руб. порция. Повышается или снижается благосостояние Ларисы в летние месяцы?
8.8. Потребитель расходует весь свой доход на приобретение трех товаров. В таблице приводятся данные о ценах и объемах потребления:
| Год | Объем потребления товаров | Цены | ||||||
| X | Y | Z | Px | Py | Pz | |||
Как изменилось благосостояние потребителя по сравнению с 2001 годом:
а) в 2002 году, б) в 2003 году.
8.9. Номинальный доход потребителя вырос на 10%, а цены продуктов питания выросли на 20%. Выросло, снизилось или не изменилось благосостояние потребителя, если до повышения цен он тратил на продукты питания ровно половину своего дохода?
8.10. До изменений в налогообложении потребитель 20% дохода тратил на основные продукты питания. Правительство отменяет налог НДС на эти продукты, в результате чего их розничная цена снижается на 10%. Одновременно повышается подоходный налог, в результате чего располагаемый доход потребителя снижается на 2%.
а) Выросло, снизилось или не изменилось благосостояние потребителя?
б) Как изменился бы ответ, если бы рост подоходного налога сократил располагаемый доход потребителя на 3%?
в) Предположим теперь, что правительство повышает НДС и снижает подоходный налог. В результате цены основных продуктов питания вырастают на 10%, а располагаемый доход возрастает на 2%. Каков будет ответ на вопрос пункта а)?
Потребителя.
4.1. Постройте бюджетные ограничения и запишите их уравнения, если:
а) Семья тратит на фрукты 30рублей, приобретая только яблоки и бананы. Цена яблок 3 рубля, цена бананов 6рублей. Что произойдет при изменении цен и суммы, запланированной на расходы?
б) Продовольственные талоны выдаются на сумму F, I – доход, p – средняя цена единицы продовольственных товаров, х – количество потребляемого продовольствия.
в) Авиакомпания предоставляет премию постоянному клиенту. Пусть I – доход клиента, p – цена 1000км перелета, Qm – минимальное расстояние, за которое предоставляется премия, Q0 – величина натуральной премии. (Подсказка: считать, что премия может быть предоставлена только 1 раз; рассмотрите случаи, когда доход клиента больше или меньше суммы, необходимой для осуществления перелета на расстояние Qm)
г) Бедным семьям предоставляется частичная скидка на оплату жилья. Размер льготной жилой площади 50 кв. метров, pS – субсидируемая цена за квадратный метр, pM – рыночная цена за квадратный метр, I – доход семьи в месяц.
4.2. Нарисуйте кривые безразличия и определите функции полезности:
а) Дошкольника Васи, который абсолютно равнодушен к овсяной каше (x) и всегда норовит отдать ее сестре, но зато готов съесть сколько угодно картофельных оладий (y).
б) Домохозяйки Марии, которая терпеть не может тараканов; испорченное настроение от каждого замеченного таракана (x) может быть поправлено только при помощи шоколадной конфеты (y).
в) Студента Валерия, считающего, что 1 гамбургер (x) прекрасно заменяют 2 пирожка с капустой (y).
г) Пенсионерки Матильды Петровны, которая по утрам пьет чай (x) исключительно с молоком (y), причем в равных пропорциях.
д) Мистера Бонда, который круглосуточно предпочитает «очень сухой мартини»: 2 части джина (x) на 1 часть вермута (y).
е) Сторонница раздельного питания Оксаны, которая употребляет либо мясо (x), либо рыбу (y), но не любит их смешивать – старается не употреблять мясные, и рыбные продукты в течение одного дня.
4.3. Определите MRSxy и нарисуйте кривые безразличия для функций полезности:
а) 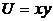 ,
, 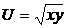 ,
,  ;
;
б) 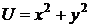 ,
, 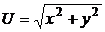 ;
;
в) 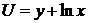 ,
, 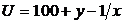 ;
;
г) 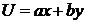 с различными коэффициентами
с различными коэффициентами 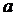 и
и 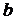 .
.
4.4. Как изменится бюджетное ограничение (в случае 2-х товаров), если на первый товар накладывается количественный (потоварный) налог t, на второй - потоварная субсидия w, и потребитель платит паушальный (подоходный) налог T? Покажите изменения графически.
4.5.
Тема 5. Оптимальный выбор потребителя.
Функции индивидуального спроса.
2.
3.
4.
5.
5.1. Определите функции спроса для ситуаций с двумя товарами и заданным доходом, если рассматриваются:
а) функция полезности Кобба-Дугласа;
б) квазилинейная функция полезности 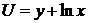 ;
;
в) абсолютно комплементарные блага;
г) совершенные заменители.
5.2. Маша имеет $240, которые она решает потратить на блага 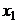 и
и 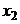 . Первый товар стоит $4 за единицу. Второй товар стоит $6 за единицу. Функция полезности:
. Первый товар стоит $4 за единицу. Второй товар стоит $6 за единицу. Функция полезности: 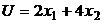 . Какой набор выберет Маша?
. Какой набор выберет Маша?
5.3. Билл[1] считает масло и маргарин абсолютно взаимозаменяемыми товарами. Его бюджет $20, цена пачки масла $2,цена пачки маргарина $1. Определите:
а) вид кривых предпочтения и функцию полезности Билла;
б) являются ли предпочтения выпуклыми;
в) оптимальный выбор Билла.
5.4. Функция полезности 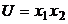 , доход потребителя $100. Цена второго блага
, доход потребителя $100. Цена второго блага 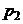 = $4. Первые 15единиц первого блага стоят по $4 за единицу, каждая дополнительная единица стоит $2. Какой набор предпочтет потребитель?
= $4. Первые 15единиц первого блага стоят по $4 за единицу, каждая дополнительная единица стоит $2. Какой набор предпочтет потребитель?
5.5. Конни1 покупает в супермаркете картофель (x) и мясо (y). Ее бюджет $200, цена мяса $4за фунт. Функция полезности: U = x + 3y. Нарисуйте бюджетное ограничение и определите оптимальный выбор Конни, если:
а) цена картофеля $2за фунт;
б) супермаркет проводит рекламную кампанию – если Конни покупает 20 фунтов картофеля, то получает еще 10 фунтов бесплатно (это правило распространяется только на первые 20 фунтов, остальной картофель продается по обычной цене $2 за фунт);
в) из-за угрозы вспышки картофельной гнили супермаркет вынужден прекратить рекламу и снизить цену на весь картофель до $1 за фунт.
5.6. Известна функция полезности 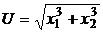 . Найдите оптимальный спрос на блага при ценах
. Найдите оптимальный спрос на блага при ценах 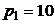 ,
, 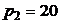 и доходе
и доходе 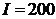 .
.
5.7. Студент изучает микроэкономику в 1 и 2 семестрах. Итоговая оценка за курс выставляется как минимальная из двух, полученных в каждом семестре. Студент имеет всего 20часов на подготовку к экзаменам в обоих семестрах. Каждые 10минут подготовки к первому экзамену дают 1балл. Каждые 20минут подготовки ко второму экзамену дают также 1балл. Как оптимально распределить время на подготовку к экзаменам? Как изменится ответ, если оценка за курс выставляется как максимальная из двух, полученных в каждом семестре?
5.8. Функция полезности 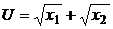 . Для заданных цен и дохода найдите оптимальный спрос на благо
. Для заданных цен и дохода найдите оптимальный спрос на благо 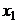 .
.
5.9. Найдите функции некомпенсированного спроса, косвенную функцию полезности, функции компенсированного спроса и функцию расходов для следующих функций полезности:
а) 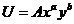 ; в)
; в) 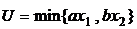 ; д)
; д) 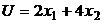 ;
;
б) 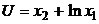 ; г)
; г) 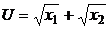 ; е)
; е) 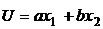 .
.
5.10. Исходя из косвенной функции полезности, найдите некомпенсированный спрос на блага, функцию расходов, функции компенсированного спроса, прямую функцию полезности в следующих случаях:
а) 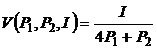 ; в)
; в) 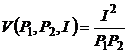 ;
;
б) 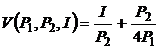 г)
г) 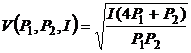 .
.
5.11. Исходя из функции расходов, найдите косвенную функцию полезности, функции некомпенсированного и компенсированного спроса, прямую функцию полезности в следующих случаях:
а) 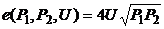 ; в)
; в) 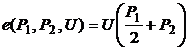 ;
;
б) 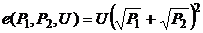 ; г)
; г) 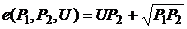 .
.
5.12. Функция полезности потребителя 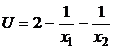 . Даны цены товаров р1, р2, а также доход I. Определите функции некомпенсированного и компенсированного спроса на блага, косвенную функцию полезности, функцию расходов. Покажите, что функции спроса однородны по ценам р1, р2 и доходу I с показателем однородности нулевой степени.
. Даны цены товаров р1, р2, а также доход I. Определите функции некомпенсированного и компенсированного спроса на блага, косвенную функцию полезности, функцию расходов. Покажите, что функции спроса однородны по ценам р1, р2 и доходу I с показателем однородности нулевой степени.
