Мир потребительских предпочтений: закономерности развития

Кривая безразличия

Попытки измерения субъективной полезнос­ти с помощью абсолютной шкалы не увен­чались успехом, поэтому ряд ученых предложили заменить абсо­лютную шкалу относительной и описать поведение потребителя с помощью предпочтения или ранжирования. Такие попытки пред­принимались в течение полувека, начиная с 80-х гг. XIX в.

Наибольший вклад в разработку ординалистской (порядковой) полезности внесли Ф. Эджуорт, В. Парето, Е. Слуцкий, Р. Аллен и Дж. Хикс. Эти ученые предложили измерять субъективную полез­ность с помощью не абсолютной (кардиналистская теория), а отно­сительной шкалы, показывающей предпочтение потребителя или ранг потребляемого блага (ординалистская, или порядковая, тео­рия полезности). При этом потребителю необходимо лишь сделать выбор между двумя наборами потребительских благ. Предпочте­ние потребителя касается всех благ, однако в целях упрощения мы рассмотрим лишь два блага (рис. 4—5).

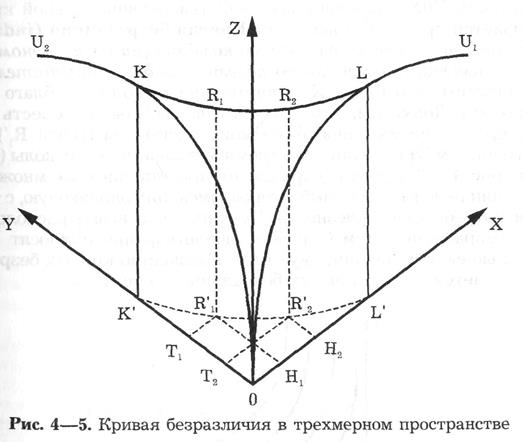
Поскольку величина полезности зависит от количества благ, то функция полезности блага X представлена кривой U₁ блага Y – U₂ Общая полезность двух благ в трехмерном пространстве может быть отложена на оси Z. Для любой точки L кривой U₁ может быть найдена такая точка К кривой U₂, обозначающая одинаковую с ней полезность для потребителя. Соединив все точки на поверхности мы получим кривую KR₁R₂L — геометрическое место точек, каждая из которых представляет одинаковые по полезности по­требительские наборы двух благ. Проекция К’R₁‘R₂‘L’ кривой KR₁R₂L на плоскость Y0Х сохраняет все свойства первоначальной кривой и называется кривой безразличия. Кривая безразличия(indifference curve)показывает различные комбинации двух экономичес­ких благ, имеющих одинаковую полезность для потребителя.

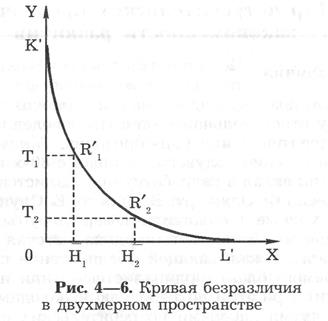
Допустим, что благо X является пепси-колой, а благо V — гамбургером. Допустим, что потребителю все равно, съесть ли 3 гамбургера, запив их одной бутылкой пепси-колы (точка R₁’), или съесть один гамбургер, запив его тремя бутылками пепси-колы (точка R₂') (см. рис. 4—6). Кривая безразличия представляет все множество комбинаций пепси-колы и гамбургеров, имеющих одинаковую, с точки зрения потребителя, полезность. Чем правее и выше расположена кривая безразличия, тем большее удовлетворение приносят пред­ставленные ею комбинации двух благ. Множество кривых безразли­чия называется картой кривых безразличия (рис. 4—7).

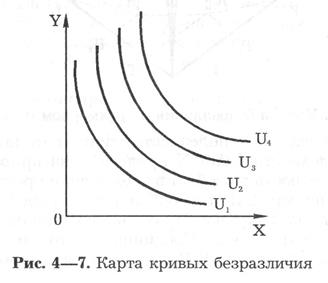
Кривые безразличия имеют отрицательный наклон, выпуклы относительно начала координат и никогда не пересекаются друг с другом. Поэтому через любую точку можно провести лишь одну кривую безразличия. Аппарат кривых безразличия имеет важное значение в теории поведения потребителя.

Зона замещения

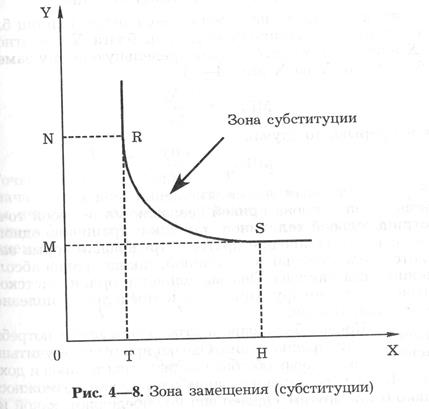
Зона замещения (субституции)- участок кривой безразличия, в котором возможна эффек­тивная замена одного блага другим.

Рассмотрим кривую безразличия RS (рис. 4—8). Количество блага X, равное 0Т, представляет минимально необходимую ве­личину потребления блага X, от которого потребитель не может отказаться, как бы ни было велико предлагаемое взамен благо Y. Аналогично 0М есть минимально необходимая величина потребления блага У. Взаимная замена благ X и Y имеет смысл только в пределах отрезка RS. Вне его замена исключается и два блага выступают как независимые друг от друга.

Предельная норма

Предельная норма замещения (marginal rate of substitution – MRS) — количество, на которое потребление одного из двух благ должно быть увеличено (или уменьшено), чтобы полностью компенси­ровать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную (предельную) единицу.

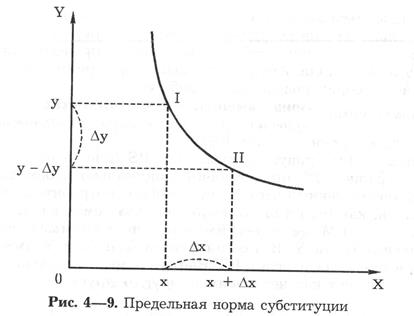
Если на оси абсцисс мы отложим количество единиц блага X, а на оси ординат — количество единиц блага Y, то отношение — ΔY/ΔХ или dу/dх характеризует предельную норму замещения (или субституции) Y на X (рис. 4—9):

(4.4)

MRS_xy = ,

(4.5)

или для непрерывного случая

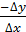MRS_xy = -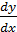

где МКS_хy — предельная норма замещения у на х.

Тангенс угла наклона кривой безразличия в любой точке яв­ляется отрицательной величиной, так как сокращению одного бла­га сооответствует увеличение другого. Предельная норма замеще­ния является положительной величиной, так как равна абсолютно­му значению угла наклона. Она выполняет в ординалистской тео­рии полезности те же функции, что и предельная полезность в кардиналистской теории.

Бюджетное ограничение

Кривые безразличия позволяют выявить потребительские предпочтения. Однако при этом не учитываются два важных обстоятельства: цены товаров и доход по­требителей. Кривые безразличия лишь показывают возможность за­мены одного блага другим. Однако они не определяют, какой именно набор товаров потребитель считает для себя наиболее выгодным. Эту информацию дает нам бюджетное ограничение(линия цен, прямая расходов — budget constraint). Оно показывает, какие потребитель­ские наборы можно приобрести за данную сумму денег. Если I — доход потребителя, Р_х — цена блага X, Р_y — цена блага Y, а X и Y составляют соответственно купленные количества благ, то уравне­ние бюджетного ограничения можно записать следующим образом:

I = P_xX + P_yY

или в более привычном виде:

(4.6)

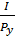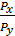Y = - X,

где –Р_x/Р_y — угловой коэффициент прямой расходов, который из­меряет наклон этой прямой к оси абсцисс.

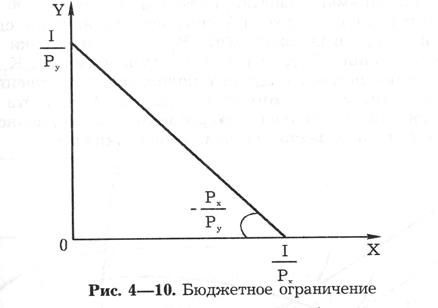
При Х=0, Y=I/Р_y, то есть весь доход потребителя расходуется на благо Y. Его количество легко подсчитать, разделив доход на цену этого блага. При Y=0 , Х=I/Р_х, то есть мы находим количество блага X, которое потребитель может купить по цене Р_x (рис. 4—10).

Точка касания кривой безразличия с бюджетным ограничени­ем означает положение равновесия потребителя. На рис. 4—11 по­казаны несколько кривых безразличия — U₁, U₂, U₃. Кривая U₁ пересекает бюджетную линию и поэтому является неоптимальным решением для потребителя.

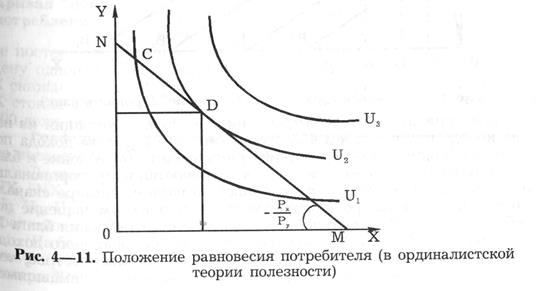
Двигаясь вдоль бюджетного ограничения, мы можем найти
такую точку D, которая принадлежит кривой безразличия U₂
более высокого порядка и в которой максимизируется благосостоянии
потребителя при данном бюджете. Кривая U₃ является кривой более,
лее высокого порядка, чем U₂, однако она выходит за пределы
нашего бюджета и поэтому пока для нас недостижима.