Решение задач и искусственный интеллект

Литература по решению задач в рамках ИИ возможно более обширна, чем по любому другому психологическому процессу. Одна из причин, почему многие специалисты по ИИ интересуются решением задач, состоит в том, что этот термин, грубо говоря, синонимичен мышлению, которое в его сложном виде является исключительно человеческим атрибутом. Этот факт, а также то, что машины с ИИ вообще способны выполнять процедуры решения задач, привело к широкому развитию методов и теории в этой области.

Вычисления были одним из первых примеров использования машин для решения задач. В 1642 году Паскаль (тогда ему было 19) продемонст­рировал, что при помощи изобретенного им механического вычислителя некоторые математические задачи можно решать точнее и быстрее, чем люди делают вручную. В контексте современного ИИ решение задач озна­чает гораздо больше, чем математические вычисления; оно охватывает широкий диапазон от решения сложных головоломок до доказательства теорем, заучивания успешных операций и различных игр.

В основе многих работ в сфере ИИ лежит важное различение между двумя методами решения задач. Один метод называется алгоритмическим, а другой — эвристическим. Алгоритмы обычно определяются как проце­дуры, гарантирующие решение задач данного типа; эвристика есть набор эмпирических правил или стратегий, которые в итоге действуют подобно правилу большого пальца. Различие между этими методами можно проил­люстрировать на примере шахматной задачи. Шахматы для компьюте­ра — это игра, в которой во всякий данный момент существует ограничен­ное количество ходов для каждого игрока. И на каждый из возможных ходов противник может ответить также ограниченным набором ходов. Для практических целей количество этих перестановок конечно — т.е. игра должна закончиться выигрышем (поражением) или вничью. На Рис. 15.12 показана часть еще более разветвленного дерева ходов, возможных в шах­матной партии. Конечно, нельзя изобразить возможные ходы для всей партии, ибо такая диаграмма содержит около 10¹²⁰ различных путей. Что­бы представить себе это огромное число возможных ходов в шахматной игре, вообразите пространство, необходимое для отображения всех этих перестановок. Если все возможные пути закодировать в виде мельчайших точек, они бы многократно заполнили все библиотеки мира! Тем не менее, алгоритмический поиск, при котором исследуются все варианты, неизбеж­но привел бы к ряду вариантов игры с выигрышем, проигрышем или ничь­ей. Не только люди, но даже и самые сложные компьютеры из всех, кото­рые только можно вообразить, неспособны воспользоваться этим мето-

Искусственный интеллект 527

дом Вместо него и люди, и компьютеры используют эвристические мето­ды поиска, при которых становится важной стратегия игры — например, атака на ферзя, контроль за центром доски, блокирование главных фигур противника, обмен с получением преимущества в позиции или фигурах и т д К обсуждению алгоритмического и эвристического поиска мы вернем­ся при рассмотрении универсального решателя задач, но сначала пого­ворим еще о компьютерных шахматах

Компьютер-ные шахма­ты

Выше мы описывали, как при помощи оптимального сканера, работающе­го с компьютером, можно было бы разобрать смысл простого паттерна методом сравнения матриц (с 506) Обсуждая анализ паттернов, мы выяс­нили, что паттерны сложны и что модель распознавания паттернов чело­веком, основанная только на сопоставлении матриц, не способна имитиро­вать разнообразие, сложность и экономичность, характерные для челове­ческой способности к распознаванию паттернов при кратком предъявле­нии

Если бы для распознавания каждого из разнообразных паттернов, встре­чающихся в повседневной жизни, нужно было иметь по отдельной матри­це, они переполнили бы емкость хранения даже самого большого компью­тера Но давайте выберем для сопоставления матриц умеренно простой паттерн — что-нибудь среднее между опознанием вашей бабушки и счи­тыванием стоимости фунта масла (код напечатан на упаковке) В шахма­тах мы имеем как раз такие паттерны простая сетка 8x8 попеременно окрашенных клеток, ходы четко определяются (например, ладья может ходить на любое количество клеток по вертикали или горизонтали при условии, что на ее пути нет других фигур, пешка может ходить на одно поле вперед, за исключением и т д ), ходы можно выбирать путем грубо­го поиска, а количество перестановок конечно, хотя и огромно При усло­вии очень большого объема хранения и такого же запаса времени можно для каждого хода определить вероятность, с которой он приближает вы-

Возможные начальные

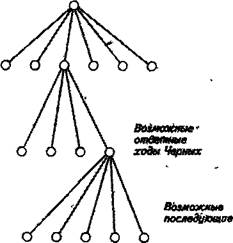
Рис. 15.12.Часть дерево вероятных ходов в шахмат­ной партии

Ответные ходы Белых

Мышление и интеллект - естественный и искусственный 528