От круглой плиты на колонну

Построить падающую тень от круглой плиты на колонну можно двумя способами.

1. Для построения начальной точки тени 1'0 следует из точки 0' на проекции оси провести дугу окружности радиусом r, равным радиусу окружности плиты. На пересечении с прямой, проведенной из точки с'под углом 45°, получим точку b', через которую проведем горизонталь, и определим на ней симметричные точки 1'0 и 3'0.

Точка тени 2'0определена лучом, проведенным из точки 2', отмечающей невидимый контур собственной тени цилиндра плиты, на невидимый контур тени колонны. Точка 4'0исчезновения тени получена засечкой дугой окружности радиусом, равным отрезку 0 - 4'. Она определена с помощью построения вспомогательной падающей тени от нижней кромки круглой плиты на «биссекторную» плоскость.

В этом построении хорошо прослеживается лучевая симметрия контура падающей тени (точки 1'0и3'0, пары точек 4'0и5'0), которые принадлежат линии пересечения лучевого цилиндра, проходящего через нижнюю кромку плиты, с цилиндрической поверхностью колонны (рис. 13).

Построение собственной тени на колонне и на круглой плите см. рис.2.

Рис. 13

2. Второй способ в построениях проще, чем первый.

Падающую тень от круглой плиты на фронтальный и профильный очерки колонны строим с помощью вспомогательного конуса с углом наклона образующих 45°, обращенного вершиной вниз и описанного вокруг нижнего основания плиты (точки 1', 2')

Высшую точку 3' падающей тени строим с помощью вспомогательного конуса с углом наклона образующих 35°. Определяем параллель, по которой вспомогательный конус пересекается с поверхностью колонны, а из вершины конуса в обратном направлении проводим луч под углом 45° до пересечения с параллелью.

Точку «исчезновения» падающей тени 4 получаем засечкой дуги окружности радиуса. равного отрезку 0-4 (рис. 14).

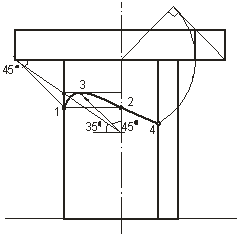
Рис. 14

На рис. 15 показано построение совмещенной тени от квадратной плиты на круглый пояс и на колонну, а также от круглого пояса на колонну.

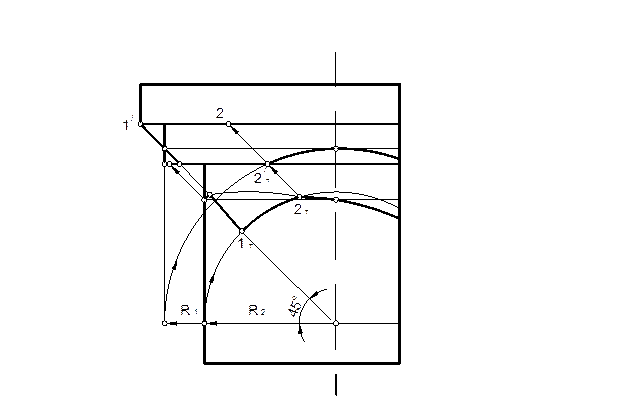
Рис. 15

Построение собственной и падающей

Тени на скоции

Рассмотрим построение собственной тени на «предельной» скоции. Форма поверхности такова, что падающей тени не будет, так как кривая очерка в верхней точке касается прямой под углом 35°.

Точки 1'и 2'построены с помощью вписанного цилиндра.

Высшая 3' и низшая 4' точки построены с помощью вписанных конусов с углом наклона образующих 35°.

Точки 5'и 6', а также точки 7'и 8' построены с помощью касательных конусов с углом наклона образующих 45°.

Для более точного построения точек касания образующих вспомогательных конусов к очерку поверхности можно воспользоваться прямыми, проведенными под углами, равными дополнительным углам (55° и 45°), из центров дуг очерка поверхности (рис. 16).

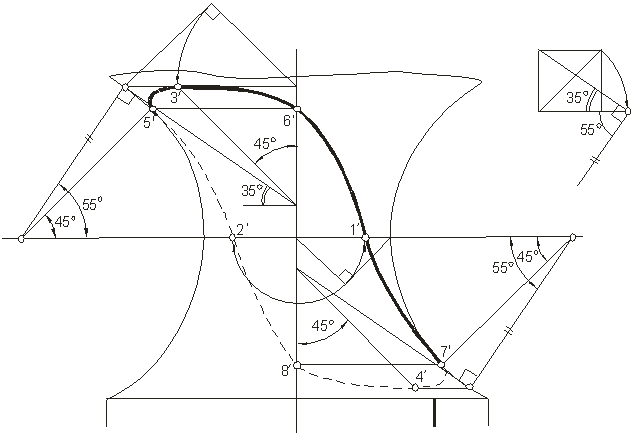
Рис. 16

На рис. 17 показано построение собственной и падающей тени на не «предельной» скоции.

Построение собственной тени аналогично рассмотренному выше.

Верхний край скоции является горизонтальной окружностью, поэтому построение падающей тени ведется согласно построению тени от круглой плиты на колонну, с использованием описанных конусов с углами наклона 45° и 35°, обращенных вершиной вниз.

Рис. 17

Построение падающей тени от тора (валика)

На колонну

Кривая собственной тени тора дает падающую тень на поверхность цилиндра тоже в виде кривой линии (рис. 18). Построение собственной тени на торе было рассмотрено выше (см. рис. 11).

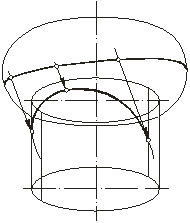
Рис. 18

Собственную тень на торе и падающую тень от тора на колонну можно построить, используя одни и те же вспомогательные касательные конусы (рис.19). С помощью касательного конуса, с углом наклона образующей 45°, обращенного вершиной вниз, строят точки a и b на поверхности тора, а также точку 1и симметричную ей, относительно лучевой плоскости, точку2на колонне. С помощью касательного конуса, с углом наклона образующей 35°, обращенного вершиной вниз, с вершиной в точке S2, строят параллели, по которым конус касается поверхности тора и цилиндра, а также точку 3– верхнюю точку падающей тени на колонне, и точкус – нижнюю точку собственной тени на поверхности тора. Точку «исчезновения» падающей тени на поверхности колонны – точку 4, строят с помощью луча, идущего из точки b(точки пересечения собственной тени тора с осью).

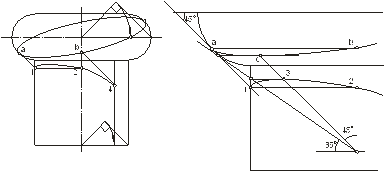
Рис. 19