Связь молекулярной массы полимера с глубиной превращения

Поскольку при поликонденсации нарастание молекулярной мас­сы полимера происходит за счет взаимодействия между собой

реак­ционных центров молекул всех реагентов системы (моно-, олиго- н n-меров) и сопровождается соответствующим уменьшением числа молекул реагентов, то можно достаточно легко установить связь между молекулярной массой образующегося продукта и глубиной превращения реакционных центров *.

Для полного описания процесса следует ввести еще следующие понятия: х.—глубина процесса по реакционным центрам; Х_М — кон­версия (глубина процесса по мономеру).

Величина x равна количеству прореагировавших реакционных центров независимо от того, кому они принадлежали (мономеру или олигомерам), и выражается долей от их исходного общего ко­личества:

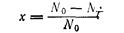
где No— исходное количество реакционных центров; N-/— количество реакцион­ных центров, оставшихся в системе к дачному моменту времени. Для бифункциональных мономеров No = 2Мо (где Мо—исход­ное количество молекул мономера). Величина Хм равна количеству вступившего в реакцию мономера, она выражается долей от его исходного количества:

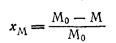
где М—количество мономера к данному моменту времени

Очень важно соотношение между х и Х_М, поскольку одному и тому же значению х могут соответствовать разные значения Х_М . На рис. 2.1 показано, что при одной и той же общей глубине пре­вращения х = 0,5 в случае Б глубина превращения по мономеру равна 1,0, в случае В—0,75. Из рисунка видно также, что в обоих случаях образовавшиеся продукты значительно различаются по длине цепи. В реальных системах существует различие соотноше­ний между х и Х_М. Основные варианты этих соотношений показа­ны на рис. 2.2.

Если Х_М = 2х, то убыль функциональных групп в системе про­исходит за счет убыли обеих функциональных групп мономера. Этому отвечает случай дубликации молекул мономера друг с дру­гом. Это типично поликонденсационный процесс.

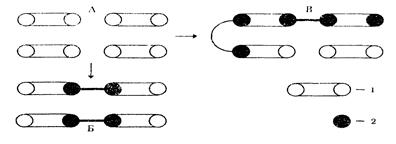
Рис. 2.1, Соотношение между глубиной превращения реакционных центров – Х и глубиной превращения по мономеру Х_М : 1—исходное состояние; Б —х = 0.5; Х_М = 1,0; В – х = 0,5; Х_М = 0.75; 1 — молекула мономера с двумя реакционными центрами; 2—прореагировавший реакционный центр.

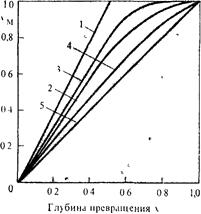
РИС 2 2 Взаимосвязь между глубиной пре­вращения по мономеру – Х_М „ и глубиной превращения по функциональным группам х для раз­личных процессов: 1—поликонденсация удвоением; 2—поликонденсация по Флори, 3 — поликонденсация мономеров с зависимыми функциональными груп­пами (k₁/k₂ > l), 4—поликонденсация мономеров с зависимыми функциональными группами (k₁/k₂ < 1), 5 —полимеризация.

Если Х_М = х, то убыль функциональных групп в системе про­исходит за счет убыли одной функциональной группы мономера, т.е. рост цепи макромолекулы происходит путем последователь­ного присоединения молекул мономера к полимерной цепи; при этом реакционная способность функциональных групп олигомеров при реакции друг с другом гораздо ниже, чем при реакции с мономером. Этому случаю соответствует полимеризационный процесс (кривая 5).

Случаю, отвечающему наиболее вероятностному варианту по­ликонденсации, т. е. равной реакционной способности всех функ­циональных групп в системе, включая мономер, соответствует кривая 2. Другие случаи поликонденсации описываются кривыми 3 и 4: кривая 3 соответствует коэффициенту взаимозависимости k₁/k₂ > l, кривая 4 — ситуации, когда k₁/k₂ < 1. (О коэффициенте взаимозависимости см. ниже.)

Совершенно очевидно, что учет суммарной степени превраще­ния х и по мономеру л:м является лишь первым шагом к деталь­ному рассмотрению поликонденсационных процессов, так как до­статочно полно описывает лишь начальную стадию. Аналогичное рассуждение можно провести для любой глубины процесса, считая конечный продукт на i-том этапе мономером для i +1) этапа. Для этого потребовалось бы ввести понятие глубины превращения по всем n-мерам. Однако решение практических задач при этом становится возможным лишь при использовании ЭВМ.

Для того чтобы связать общую глубину превращения реакцион­ных центров с молекулярной массой образовавшегося к данному моменту продукта, необходимо знать, каким продуктам принадле­жат непрореагировавшие реакционные центры (концевые группы). Очевидно, что для реальных систем с большим количеством моле­кул это сделать довольно трудно. Поэтому для вывода уравнения, связывающего молекулярную массу (степень поликонденсации) полимера с глубиной превращения, пользуются упрощенной мо­делью поликонденсации (так называемая поликонденсация дубликацией или удвоением). При этом вводятся следующие упроще­ния:

процесса поликонденсации условно разбивается на несколько этапов;

предполагается, что на каждом этапе реагируют друг с другом лишь одинаковые (по степени поликонденсации) продукты;

результатом каждого этапа является получение продукта с уд­военной степенью поликонденсации (удвоение, дубликация);

образовавшиеся продукты с удвоенной степенью поликонден­сации на данном этапе не реагируют, а «ждут» следующего этапа. .

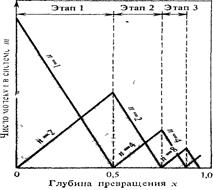
Нереальность такой модели достаточно очевидна, тем не менее на ее основе получены результаты, довольно хорошо описываю­щие простейшие случаи поликонденсации. Протекание процесса поликонденсации путем удвоения наглядно показано в табл. 2.1 и на рис. 2.6. На первом этапе происходит исчезновение мономера (/г==1) и образование димера (л ==2); на втором—убыль димера соот­ветствует появлению тетрамера и т. д

Из рис. 2.6 сразу видна искусственность приема удвоения (дуб­ликации): не учитывается образование промежуточных продуктов нечетных степеней поликонденсации и, пожалуй, самое главное, появление продуктов на предыдущих этапах; октамер (n == 8) по­является лишь на третьем этапе (на самом деле в некоторых ко­личествах он может образоваться и на втором и даже на первом этапе). Для любого процесса образования полимера будет справедли­во следующее выражение для степени поликонденсации:

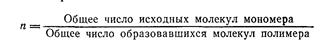
Число образовавшихся линейных макромолекул равно числу концевых групп, деленному на два. Для глубины превращения более 0,5 количество концевых групп равно количеству непрореагировавших функциональных групп, т.е. N_o(l—х). Следовательно:

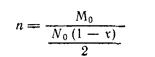
или, поскольку для бифункциональных мономеров N_o == 2M_o, то

n = 1/(1-x) (2.1)

Можно использовать и другую форму этого уравнения, являю­щуюся более удобной и рациональной:

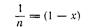(2.2)

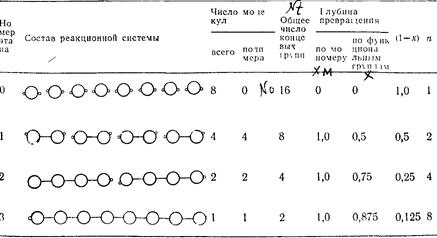
Это уравнение выводится непосредственно из данных табл. 2.1, из которых видно, что степень поликонденсации изменяется в

за­висимости от номера этапа по закону возрастающей геометриче­ской прогрессии со знаменателем 2, величина (1—х) зависит от номера этапа по закону убывающей прогрессии со знаменателем 1/2. Совместно решение этих уравнений дает уравнение 2.1

РИС 2 3. Зависимость числа молекул в системе от глубины процесса.

РИС 2.4 Зависимость степени поликонденсации (1) и обратной степени поликонденсации (3) от глубины превращения.

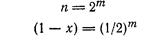
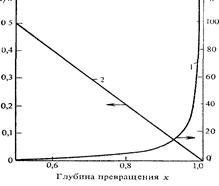
Зависимость n от x, рассчитанная по уравнениям 2.1 и 2.2 приведена на рис. 2.4. Из рисунка 2.4 видно, что для процессов поликонденсации характерно резкое возрастание степени поликонден­-

сации полимера с увеличением глубины процесса, что было качественно получено нами ранее (см. рис.1.3).

Очень важно, что в координатах обратная степень поликонден­сации—глубина превращения (1/n—х) зависимость, выражае­мая уравнением (2.1), становится линейной (прямая 2 на рис. 2.4). На основе этой зависимости достаточно просто получать аналитические выражения для других закономерностей поликонден­сации.

ТАБЛИЦА 2 1

Поликонденсация дубликацией (удвоением)

По поводу уравнения (2.1) следует сделать несколько поясне­ний. Степень поликонденсации, определяемая уравнением (2.1), вследствие вероятностного характера процесса является средней величиной, причем для начальных стадий процесса она может рав­няться единице. Однако уравнение (2.1) не учитывает, по каким причинам в данный момент времени (чаще всего в конце процес­са) глубина поликонденсации оказалась равной х. Поскольку величина х лежит между крайними значениями (0 и 1), то данное значение х может быть как следствием развития процесса от 0 до х (определяется кинетикой), так и следствием того, что в данных условиях

процесс не может быть осуществлен до х == 1,0. Это может произойти по достижении термодинамиче­ского равновесия, из-за взаимодействия функциональных групп с монофункциональными соединениями, прекращения процесса, на­пример, вследствие высокой вязкости среды и т. д.

Уравнение (2.1) пригодно для описания как поликонденсации мономеров (типов а—а и b—b), так и поликонденсации сомономеров при их эквимольных количествах в исходной смеси. На первой стадии сомономеры типа а—а взаимодействуют с образованием димера, строение которого аналогично строению мономера типа а—b, например

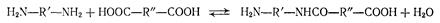
Дальнейшая поликонденсация сомономеров полностью аналогич­на поликонденсации мономеров типа а—b.

Поскольку в уравнение (2.1) не входит время, то его можно применять для многих процессов поликонденсации независимо от их скорости и других кинетических особенностей.

В уравнение (2.1) не входит содержание исходного мономера (функциональных групп), оно учитывается величиной х. При син­тезе линейных полимеров глубина превращения никогда не будет равна 1,0, так как даже при образовании одной макромолекулы из всего мономера в системе останутся непрореагировавшими две функциональные группы, принадлежащие концам этой макромо­лекулы, т. е. предельное значение х равно:

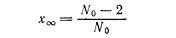
Завершая анализ уравнения (2.1), следует вновь подчеркнуть, что метод удвоения, положенный в основу его вывода, является искусственным приемом описания поликонденсации, позволяющий, однако, учесть специфику процесса. Ценность этого приема состоит в том, что он не учитывает хи­мическую природу процесса. Поэтому изложенные выше выводы могут быть плодотворно использованы при рассмотрении самых различных процессов поликонденсации: ионных, радикальных и т.д.

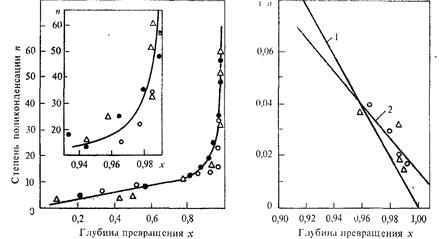
РИС. 2.5. Зависимость степени поликонденсации от глубины процесса при взаимодействии 4,4'–диoкcндифeнилпpoпaнa и дифеяилкарбоната в расплаве: O—182°С;D—198; ·—21(i°C

РИС. 2.6. Зависимость обратной степени поликонденсации от глубины превращения функци­ональных групп при синтезе поликарбонатов в расплаве[по G]: 1 — прямая рассчитана по уравнению (2.1); 2 —прямая рассчитана по уравнению (25) при Х,=:0,68 и С=-0,33;O—182°С;D—198°С (экспериментальные точки).

Несмотря на приближения, допущенные при выводе уравнения (2.1), его следует считать основным уравнением поликонденсационных процессов, так как оно верно передает самую суть процесса.

Экспериментальная зависимость n от х для процесса поликонденсации поликарбоната в расплаве приведена на рис. 2.5. Из ри­сунка видно, что степень поликонденсации полимера возрастает с глубиной процесса, и особенно резко при глубине, близкой к 1,0 (100%). Сравнение экспериментальных данных с данными, рассчи­танными по уравнению (2.1) и (2.5), приведено на рис. 2.6. В наи­более важной области (х = 0,9—1,0) указанное уравнение до­

статочно хорошо описывает экспериментальные данные. Отсюда вытекают важнейшие требования к проведению технологического процесса поликонденсации. В большинстве случаев бывает необ­ходимо применять такие технологические приемы и такую аппара­туру, которые обеспечили бы протекание поликонденсации на большую глубину. Из обычных приемов следует отметить следую­щие: увеличение продолжительности процесса, повышение темпе­ратуры процесса, обеспечение полного удаления низкомолекуляр­ного продукта реакции, использование катализаторов, мономеров с повышенной активностью функциональных групп.

Как уравнение (2.1), так и сам метод удвоения не позво­ляют учитывать различия в реакционной способности мономеров, олигомеров и полимеров. Между тем это различие может вызвать существенное отклонение от статистического (вероятностного) ха­рактера процесса и привести к изменению его закономерностей.