Основные свойства биномиальных коэффициентов

Свойство 1. .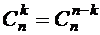

Доказательство. Рассмотрим множество из n элементов 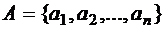. Каждому 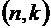–сочетанию 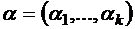однозначно соответствует 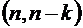–сочетание 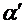, составленное из элементов множества 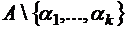. Отсюда следует, что число 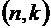–сочетаний и число 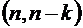–сочетаний одинаково.

Убедиться в справедливости свойства 1 можно также непосредственной проверкой, расписав число сочетаний по теореме 4.

Свойство 2. .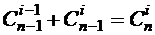

Доказательство. Свойство доказывается непосредственной проверкой. Согласно теореме 4 имеем 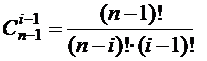, 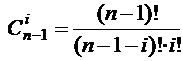. Отсюда получаем, что

.

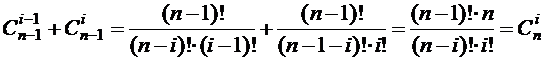Свойство 3.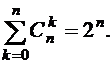

Доказательство. Пусть 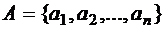. Число всех подмножеств множества А равно 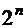, число всех k–элементных подмножеств множества А равно 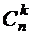, тогда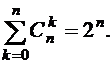

§5. Бином Ньютона

Теорема 5. .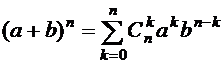

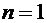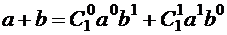Доказательство. Утверждение доказывается индукцией по n. При имеем , т.е. утверждение выполнено.

Пусть утверждение выполнено для любого 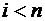. Имеем 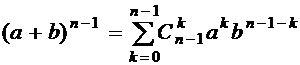по предложению индукции.

Тогда 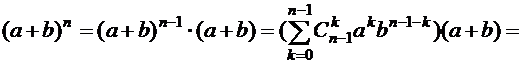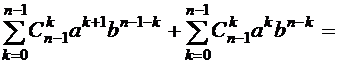(в первой обобщенной сумме выделим последнее слагаемое, а во второй – первое, получим) =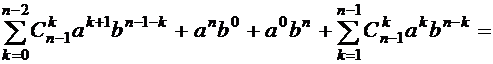

(после замены k на 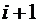в последнем слагаемом получим) =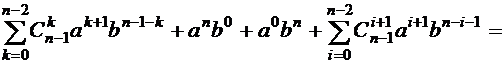

(в последнем слагаемом заменим i на k, объединим слагаемые) =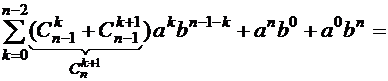

(воспользовались свойством 2 для сочетаний)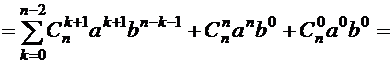

(наконец, после замены k на 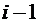получаем) = 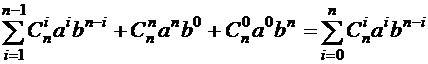. Теорема доказана.

Следствие 1. .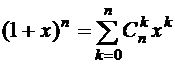

Следствие 2. .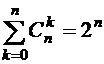

Утверждение следует из теоремы при условии, что .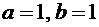

Следствие 3. .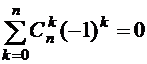

Утверждение следует из теоремы при условии, что .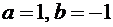

Следствие 4. .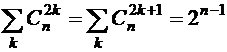

Разбиение множества

Множества 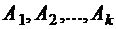задают разбиение множества А, если объединение всех множеств равно А и все множества попарно не пересекаются, т.е. 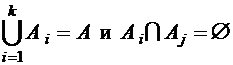для всех .

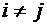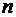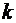Теорема 6. Число различных упорядоченных разбиений множества А мощности на подмножеств 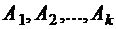заданных мощностей 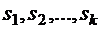равно .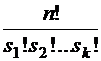

Доказательство. Пусть 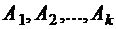─ некоторое разбиение множества А на 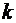подмножеств, причем 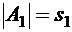, , 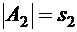…, , 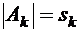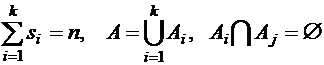для всех 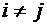. Множество 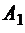может быть выбрано 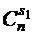способами, после выбора 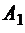множество 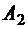может быть выбрано 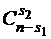способами и т.д. После выбора множеств 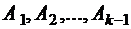множество 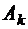может быть выбра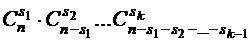но способами. Тогда по правилу произведений получаем, что общее число разбиений равно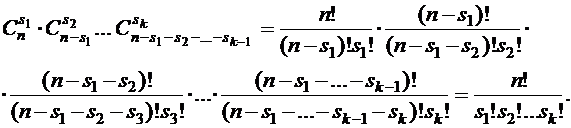

Теорема доказана.

Число 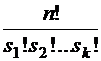называется полиномиальным коэффициентом и обозначается через .

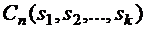Теорема 7. Если множества 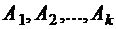задают разбиение множества А, тогда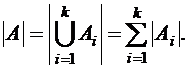

Доказательство. Рассмотрим диаграмму Венна k–го порядка для множеств 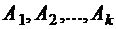. Так как 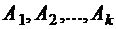задают разбиение множества А, то 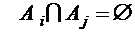для всех 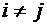, т.е. все элементы 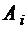расположены в одной ячейке 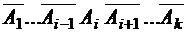. Получаем, что 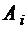= 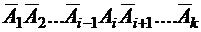. Тогда .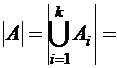

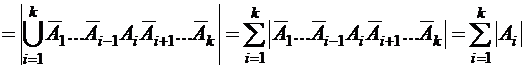Следствие. Если множества 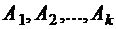не пересекаются, то

.

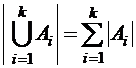Это следствие представляет собой обобщенное правило суммы.

Задача 5. Дано множество U из 9 элементов. Каким числом способов в нем можно выбрать три подмножества A, B, C так, чтобы выполнялись условия: , .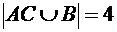

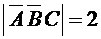Решение. Построим диаграмму Венна для искомых подмножеств A, B, C универсального множества U (см. рис.1). Введем обозначения: , , .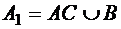

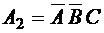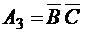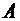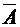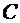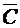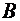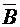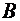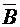Рис.1

Заметим, что 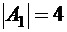(это подмножество размещено в пяти ячейках диаграммы Венна – горизонтальная штриховка), 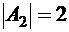(одна ячейка диаграммы – вертикальная штриховка) и 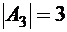(две ячейки диаграммы), причем подмножества 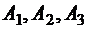задают разбиение множества U. Тогда по правилу произведения получаем, что число способов выбора подмножеств A, B, C равно .

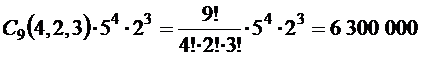§7. Перестановки с фиксированным числом повторений

Пусть 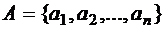. Упорядоченную 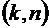−выборку 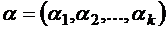c повторениями, где 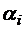встречается 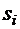раз для всех 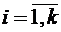, назовем перестановкой с повторениями. Число всех таких перестановок обозначим через .

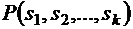Теорема 8.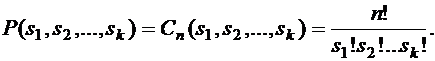

Доказательство. Пусть 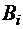− множество номеров мест, на которых стоит элемент 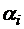в перестановке a.

Число всех перестановок с повторениями совпадает с числом всех разбиений множества 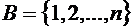на подмножества 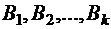, где 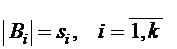. По теореме 6 получаем, что число всех разбиений 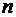–элементного множества на k подмножеств равно 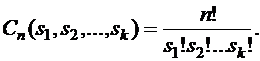Отсюда получаем, что 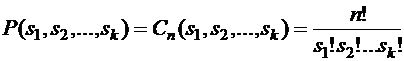, что и требовалось доказать.

Задача 6. Сколько различных слов можно составить, переставляя буквы слова «математика»?

Решение. В слове «математика» буква «м» встречается 2 раза, буква «а» – 3 раза, буква «т» – 2 раза, буква «е» – 1 раз, буква «и» - 1 раз, буква «к» – 1 раз. Всего в слове 10 букв, тогда число всех различных слов равно .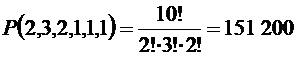

Задача 7. Сколько слов длины 9 в алфавите 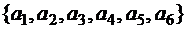можно составить при условии, что 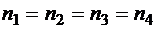, где 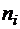обозначает число вхождений буквы 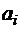в слово.

Решение. Если 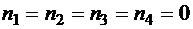, тогда 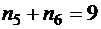, и число слов, удовлетворяющих этому условию, равно числу двоичных последовательностей длины 9.

Если 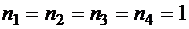, тогда 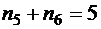, и, рассматривая всевозможные разложения числа 5 на упорядоченную сумму двух слагаемых, получаем, что число слов в этом случае равно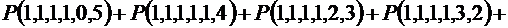

= .

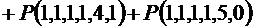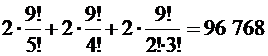Наконец, если 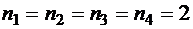, тогда 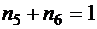, и число слов равно .

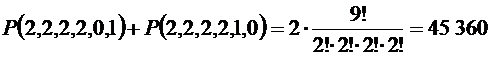По правилу суммы получаем, что всего можно составить 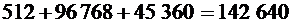слов.

Задача 8. Сколькими способами можно переставить буквы слова «комиссия» так, чтобы:

1) никакие две гласные не стояли рядом;

2) не менялся порядок гласных букв;

3) две буквы «с» не шли подряд?

Решение. 1) Имеется 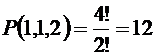перестановок согласных. Для каждого размещения согласных имеем 5 мест для размещения четырех гласных слова, тогда число всех размещений гласных букв слова равно 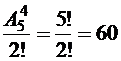. По правилу произведения получаем 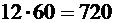слов.

2) Число размещений согласных букв с учетом того, что буква «c» повторяется дважды равно 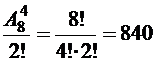. Очевидно, что на оставшиеся места гласные в указанном порядке размещаются однозначно.

3) Число различных слов, которые получаются перестановками букв слова «комиссия» равно .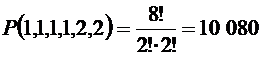

Число слов, в которых две буквы «с» идут подряд равно 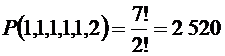. Получаем, 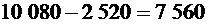слов, в которых две буквы «с» не идут подряд.

Задача 9. Сколькими способами можно разместить n одинаковых карандашей в k различных ящиках?

Решение. Перенумеруем ящики. Обозначим через 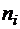− число карандашей, попавших в 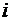−ый ящик. Каждому размещению карандашей поставим в соответствие последовательность из нулей и единиц следующим образом: сначала записываем 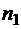нулей, затем записываем единицу, далее пишем 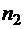нулей, снова единицу, и т.д. Заканчивается последовательность 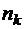нулями. Эта последовательность имеет 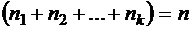нулей и 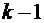единиц.

Например, при 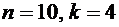размещению, при котором в первом ящике 5 карандашей, во втором – нет карандашей, в третьем ящике – 3 карандаша, а в четвертом – 2 карандаша, соответствует последовательность 0000011000100.

Таким образом, число всех размещений совпадает с числом всех двоичных наборов с n нулями и 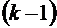единицами. Число таких наборов, в силу теоремы 8, равно .

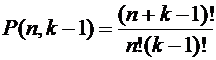Задача 10. Сколько решений в неотрицательных целых числах имеет уравнение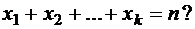

Решение. Пусть 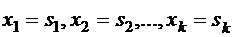решение уравнения. Этому решению поставим в соответствие двоичный набор с n нулями и 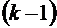единицами следующим образом:

.

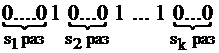Таким образом, между множеством двоичных наборов с n нулями и 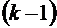единицами и множеством решений заданного уравнения устанавливается взаимно-однозначное соответствие, откуда число решений равно .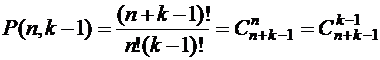