Глава 5. Нормирующие преобразования видимого объема

Видимый объем

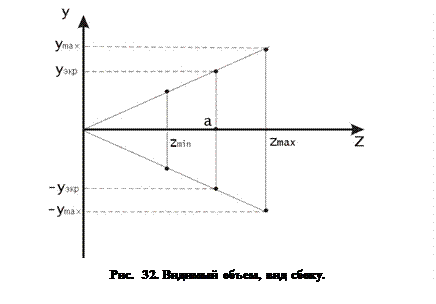
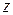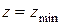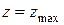Зададим центральную перспективную проекцию с центром проекции в начале координат, как показано на рис. 32. Для реальных вычислений необходимо также определить значения минимальной и максимальной отсекающих плоскостей по координате : и , соответственно.

Границы экрана, или окна вывода задают четыре отсекающих плоскости сверху, снизу, справа и слева. Таким образом, изображение, получаемое с помощью нашей проекции может находится только внутри усеченной пирамиды образованной упомянутыми плоскостями, причем объекты вне этой пирамиды не проецируются на экран, т.е. являются невидимыми для наблюдателя. Видимым объемом называется замкнутая область пространства, объекты внутри которой проецируются на экран. В случае центральной перспективной проекции видимым объемом является усеченная пирамида.

Одной из важных задач компьютерной графики является нахождение эффективного способа отсечения трехмерных объектов по границе видимого объема и удаление невидимых ребер и граней. Например, в случае центральной перспективы, для решения задачи отсечения пришлось бы для каждой грани или ребра находить точки пересечения с плоскостями усеченной пирамиды, что в общем случае потребовало бы значительных вычислений. Решение заключается в преобразовании видимого объема к виду, в котором вычисления проводились бы значительно проще. В общем идея заключается в том, чтобы свести преобразование центральной перспективы математически к виду параллельной проекции, в которой, очевидно, операция взятия проекции сводится к простому отбрасыванию у точек координаты .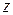

Нормирование

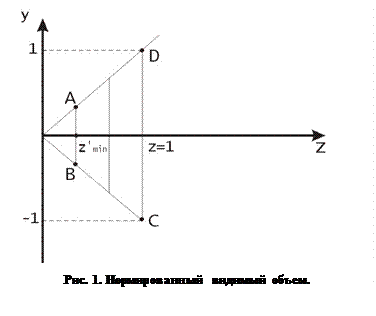
Будем решать задачу в два этапа. В начале приведем видимый объем к нормированному виду. При этом значение 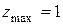, а границы по осям 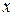и 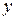лежат в диапазоне 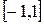, как показано на рис. 33.

Нормирующим преобразованием в этом случае будет операция масштабирования, которая для произвольной точки 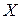выражается в виде:

,

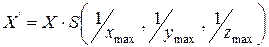где 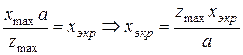, и соответственно, .

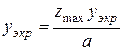Нормированный видимый объем позволяет с большей легкостью решать задачу отсечения по границе. А именно, в этом случае может применяться модифицированный вариант алгоритма Коэна-Сазарленда в котором вместо 4-битовых используются 6-битовые коды вне/внутри для описания нахождения точки в соответствующей области пространства. Уравнения боковых граней видимого объема сильно упрощаются, например, для правой отсекающей плоскости уравнение запишется 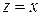, а для левой боковой 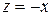и т.д. . Тогда для некоторой точки 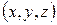условие установления бита в единицу будет следующим:

1-й бит: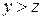

2-й бит: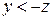

3-й бит: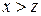

4-й бит: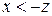

5-й бит: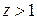

6-й бит: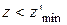

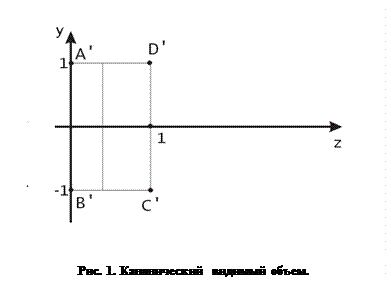Для эффективного решения задачи удаления невидимых ребер/граней преобразуем нормированный видимый объем к каноническому виду, как показано на рис. 34.

Это достигается с помощью матрицы

.

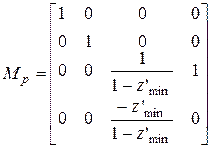После применения матрицы 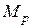нормированный видимый объем становится прямоугольным параллелепипедом, что позволяет перейти от центральной перспективной к параллельной проекции. Легко проверить, что как показано на рис. 33 и рис. 34: 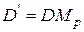, , 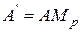, , 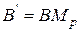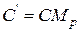а также, например, .

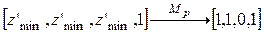Итак, нормирующие преобразования видимого объема могут производиться за два шага.

1 шаг - преобразование к нормированному видимому объему и отсечение по 3-х мерному алгоритму Коэна-Сазерленда.

2 шаг - преобразование к прямоугольному параллелепипеду с помощью матрицы 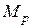и удаление скрытых поверхностей при условии равенства координат 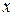и 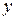.