Решение. Находимточечные оценки a и s:
Находимточечные оценки a и s:
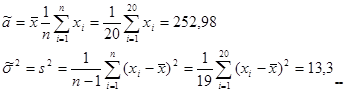
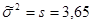
Определяем по таблице распределения Стьюдента для доверительной вероятности b=0,95 и числу степеней свободы (n-1)=19 соответствующее значение tb=2,093 и по формуле находим искомый интервал:
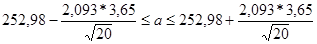
или 251,27£ а£ 254,69.
Задача 2. Разыграть 8 значений дискретной случайной величины, заданной законом распределения:
Х 3 11 24
р 0,25 0,16 0,59
Решение.
1). Разобьем интервал (0,1) оси Or точками с координатами: 0,25; 0,25+0,16 = 0,41; на 3 частичных интервала: d1 – (0; 0,25), d2 – (0,25; 0,41),
d3 – (0,41; 1).
2). Выпишем из таблицы 8 случайных чисел, например: 0,10; 0,37; 0,08; 0,99; 0,12; 0,66; 0,31; 0,85.
Случайное число r1 = 0,10 принадлежит частичному интервалу d1, поэтому разыгрываемая дискретная случайная величина приняла значение х1 = 3. Аналогично получим остальные возможные значения.
Задачи для внеаудиторной и аудиторной самостоятельной работы: 8.1.-8.20..
- Задачи для самостоятельного решения
Случайные события
