Законы взаимодействия и движениия тел

25.11.2014

Урок (10 класс)

Тема. Сила тяжести

Законы взаимодействия и движениия тел

Как Вы знаете открыл закон всемирного тяготения английский ученый Исаак Ньютон в 1667 году. Свое открытие И. Ньютон обосновал на астрономических наблюдениях. Эти астрономические наблюдения были сделаны датским астрономом Тихо Браге. Тихо Браге измерил положение всех на тот момент известных планет и записал их координаты, но вывести окончательно, создать закон движения планет относительно Солнца Тихо Браге не удалось. Это сделал его ученик Иоганн Кеплер. Иоганн Кеплер воспользовался не только измерениями Тихо Браге, но и к тому времени уже достаточно обоснованной, используемой везде и всюду гелиоцентрической системой мира Коперника. Той системой, в которой считается, что в центре нашей системы находится Солнце и вокруг него обращаются планеты.

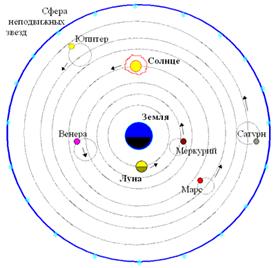
Рис. 1. Гелиоцентрическая система мира (система Коперника)

Одновременно с выводом закона всемирного тяготения появилось несколько вопросов, например, почему те или иные тела притягиваются друг к другу и каким свойствам должны отвечать эти тела. Почему они создают вокруг себя нечто, что заставляет другие тела двигаться относительно них с тем условием, которое мы рассматриваем. Отвечать на эти вопросы пришлось Ньютону, и он быстро нашел на них ответы. В первую очередь Ньютон предположил, что все тела обладают свойством притяжения, т.е. те тела, которые обладают массами, притягиваются друг к другу. Это явление стали называть всемирным тяготением. А тела, которые притягивают друг к другу другие, создают силу. Эту силу, с которой тела притягиваются, стали называть гравитационной (от слова gravitas – «тяжесть»). Ньютону удалось получить формулу для вычисления силы взаимодействия тел, обладающих массами. Обычно именно эту формулу и называют законом всемирного тяготения. Сам закон всемирного тяготения обычно звучит так: два тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.

Давайте рассмотрим величины, которые входят в этот закон. Итак, сам закон всемирного тяготения выглядит следующим образом:

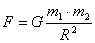F – [H], m – [кг], R – [м]

Здесь есть еще одна величина – G, гравитационная постоянная. Ее физический смысл заключается в том, что она показывает, с какой силой взаимодействуют два тела массой в 1 кг, каждый в 1 кг, расположенные на расстоянии 1 м. Обращаю ваше внимание, что эта величина очень маленькая, она всего лишь по порядку величины составляет 10^-11.

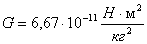
2. Ускорение свободного падения

На предыдущем уроке мы обсудили вопрос, связанный с законом всемирного тяготения. Теперь перед нами стоит задача рассмотреть, как этот закон связан с уже известным ускорением свободного падения. Ускорение свободного падения впервые определил итальянский ученый Галилео Галилей. Как вы помните, он измерял ускорение движения тел, которые двигались по наклонной плоскости, и ему удалось установить, что предельное ускорение таких тел (а это и есть ускорение свободного падения) составляет 9,8 м/с².

Частным, но крайне важным для нас видом силы всемирного тяготения является сила притяжения тел к Земле. Эту силу называют силой тяжести. Согласно закону всемирного тяготения, она выражается формулой

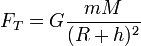, (1)

где m – масса тела, М – масса Земли, R – радиус Земли, h – высота тела над поверхностью Земли. Сила тяжести направлена вертикально вниз, к центру Земли.

Более точно, помимо этой силы, в системе отсчета, связанной с Землей, на тело действует центробежная сила инерции 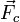, которая возникает из-за суточного вращения Земли, и равна 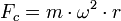, где m – масса тела; r – расстояние между телом и земной осью. Если высота тела над поверхностью Земли мала по сравнению с ее радиусом, то 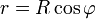, где R – радиус Земли, φ – географическая широта, на которой находится тело (рис. 1). С учетом этого .

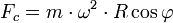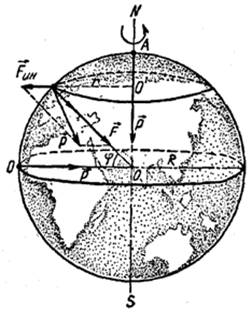
Рис. 2

Сила тяжести

Силой тяжести называется сила, действующая на любое находящееся вблизи земной поверхности тело.

Направление силы тяжести является направлением вертикали в данном пункте земной поверхности.

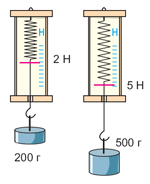
На рисунке изображён опыт с двумя гирями и динамометрами. Вы видите, что при массе гири 200 г (то есть 0,2 кг) на неё действует сила тяжести 2 Н, а при массе 500 г (то есть 0,5 кг) – сила тяжести 5 Н. Обратим внимание на закономерность:

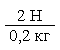= 10 Н/кг

и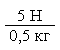

= 10 Н/кг

Проделав опыты с многими телами, мы обнаружим ту же самую закономерность: отношение силы тяжести, действующей на тело, к массе этого тела является постоянной величиной, не зависящей ни от силы тяжести, ни от массы тела. Эту величину называют коэффициентом силы тяжести:

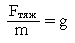Формулу для вычисления коэффициента «g» можно преобразовать, поместив слева силу тяжести:

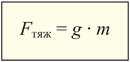Fтяж – сила тяжести, Н m – масса тела, кг g – коэффициент, Н/кг

4.Вывод формулы для ускорения свободного падения на основании закона всемирного тяготения

Однако, почему именно такое значение у этого ускорения, стало ясно только после открытия закона всемирного тяготения. Вспомним, что сила тяжести на Земле – это действие закона всемирного тяготения для тел, которые находятся на поверхности Земли. Обратите внимание на случай взаимодействия произвольного тела на поверхности Земли с самой Землей.

Рис. 3. Сила тяжести, действующая на тело на Земле

При этом вся масса Земли условно полагается сосредоточенной в ее центре. Радиус Земли – это расстояние между телами. Само тело, которое находится над поверхностью Земли, – то самое тело, которое притягивается. Давайте посмотрим, как это записывается, и обсудим результат.

Сила тяжести на Земле:

F = m ^.g

Закон всемирного тяготения в данном случае имеет вид: 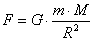. Здесь М – масса Земли, m – масса тела, R – радиус Земли, G – гравитационная постоянная. Если сравнить выражение для силы тяжести и для гравитационной силы, получим для ускорения свободного падения: .

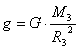Обратите внимание: ускорение свободного падения зависит от массы Земли и от радиуса Земли. Если они будут изменяться, значит, будет изменяться и ускорение свободного падения.

5. Зависимость ускорения свободного падения от географической широты и других параметров. Искусственные спутники Земли

Как известно, Земля по форме – неидеальный шар, а тело, которое немного сплюснуто с полюсов, поэтому полярный радиус несколько меньше, чем экваториальный. В этом случае надо понимать, что ускорение свободного падения на полюсе будет больше, а на экваторе будет меньше. В общем случае ускорение свободного падения зависит от широты местности.

Необходимо отметить еще вот что. Земля вращается, и вращательное движение Земли тоже влияет на ускорение свободного падения. Ускорение свободного падения на экваторе будет отличаться еще и по этой причине. Изменение ускорения свободного падения по всем вышеуказанным причинам достаточно незначительное, поэтому мы считаем, что величина ускорения свободного падения на Земле – величина постоянная и составляет g_з = 9,8 м/с².

Как видите, ускорение свободного падения зависит от радиуса Земли, значит, если увеличивать радиус, то ускорение свободного падения будет уменьшаться. Как такое может быть? Если мы поднимаем тело над поверхностью Земли (например, тот же спутник), то расстояние будет определяться суммой радиуса Земли и высоты над ее поверхностью. В этом случае ускорение свободного падения тоже будет уменьшаться.

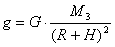
Ускорение свободного падения обратно пропорционально квадрату расстояния. Поэтому если высота будет равна радиусу Земли, то расстояние будет в 2 раза больше от центра Земли, чем для тела на поверхности, и в этом случае ускорение свободного падения уменьшиться в 4 раза.

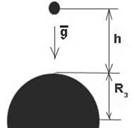
Рис. 4. К вопросу об ускорении свободного падения для тела, находящегося на определенной высоте над Землей

В опыте с двумя гирями мы выяснили, что вблизи поверхности Земли коэффициент «g» имеет значение 10 Н/кг (более точные значения 9,78 Н/кг и 9,83 Н/кг – см. далее в таблице).

Опыты показывают, что по мере удаления от Земли сила тяжести ослабевает. Например, на высоте 300 км значение коэффициента «g» уменьшается приблизительно до 9 Н/кг.

Повторяя опыт с гирями и динамометрами в различных местах Земли, а также на поверхности Луны, Марса и так далее, можно выяснить, что коэффициент «g» зависит от места наблюдения:

Коэффициенты силы тяжести, Н/кг

Луна	1,7		Земля:	» 10
Марс	3,8	а) полюс	9,83
Юпитер		б) экватор	9,78

С учетом выражения (1) для модуля ускорения свободного падения будем иметь

. (2)

На поверхности Земли (h = 0) модуль ускорения свободного падения равен

,

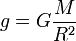Модуль ускорения свободного падения, входящего в формулы, равен приближенно 9,8 м/с².

Из формулы (2) видно, что ускорение свободного падения не зависит от массы тела. Оно уменьшается при подъеме тела над поверхностью Земли: ускорение свободного падения обратно пропорционально квадрату расстояния тела от центра Земли.

Однако если высота h тела над поверхностью Земли не превышает 100 км, то при расчетах, допускающих погрешность ≈ 1,5%, этой высотой можно пренебречь по сравнению с радиусом Земли (R = 6370 км). Ускорение свободного падения на высотах до 100 км можно считать постоянным и равным 9,8 м/с².

И все же у поверхности Земли ускорение свободного падения не везде одинаково. Оно зависит от географической широты: больше на полюсах Земли, чем на экваторе. Дело в том, что земной шар несколько сплюснут у полюсов. Экваториальный радиус Земли больше полярного на 21 км.

Другой, более существенной причиной зависимости ускорения свободного падения от географической широты является вращение Земли. Второй закон Ньютона справедлив в инерциальной системе отсчета. Такой системой является, например, гелиоцентрическая система. Систему же отсчета, связанную с Землей, строго говоря, нельзя считать инерциальной. Земля вращается вокруг своей оси и движется по замкнутой орбите вокруг Солнца.

Вращение Земли и сплюснутость ее у полюсов приводит к тому, что ускорение свободного падения относительно геоцентрической системы отсчета на разных широтах различно: на полюсах g_пол ≈ 9,83 м/с², на экваторе g_экв ≈ 9,78 м/с², на широте 45° g ≈ 9,81 м/с². Впрочем, в наших расчетах мы будем считать ускорение свободного падения приближенно равным 9,8 м/с².

Из-за вращения Земли вокруг своей оси ускорение свободного падения во всех местах, кроме экватора и полюсов, не направлено точно к центру Земли.

Кроме того, ускорение свободного падения зависит от плотности пород, залегающих в недрах Земли. В районах, где залегают породы, плотность которых больше средней плотности Земли (например, железная руда), g больше. А там, где имеются залежи нефти, g меньше. Этим пользуются геологи при поиске полезных ископаемых.

Домашнее задание

1. Е.В. Коршак, А.И. Ляшенко, В.Ф. Савченко. Физика. 10 класс, «Генеза», 2010. Повторить §19 (с.63-66).

2. Решить задачи № 3, 4 упражнения 10 (с. 66).

3. Учить лекционный материал.