Оценка снизу для остаточного члена имеет вид
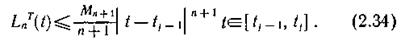
Пример 2.4. Определим шаг равномерной дискретизации на основе многочлена Тейлора нулевой степени.
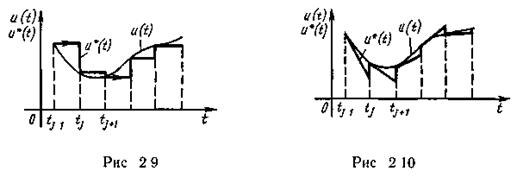
Значение восстанавливающей функции u*(t) в любой момент времени t на каждом j-м интервале tj-1 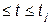 , принимается равным u(tj-1) (рис. 2.9).
, принимается равным u(tj-1) (рис. 2.9).
Значение остаточного члена L 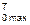 достигает максимума в конце интервала (при t=tj):
достигает максимума в конце интервала (при t=tj):

поэтому шаг дискретизации должен удовлетворять условию
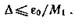
Пример 2.5. Определим шаг равномерной дискретизации с по мощью многочлена Тейлора первой степени.
При восстановлении сигнала u(t) помимо отсчета u(t0) используется значение первой производной в момент времени t0 - u'(to)
Максимум значения остаточного члена
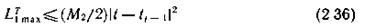
достигается при t = tj, Соответственно получаем соотношение для шага дискретизации

Восстановление сигнала происходит без задержки во времени (рис 2.10) Однако по сравнению с интерполяционным методом (пример 2.3) для него требуется вдвое большее число отсчетов
§ 2.9. АДАПТИВНАЯ ДИСКРЕТИЗАЦИЯ
Если ранее рассмотренные методы и алгоритмы дискретизации были рассчитаны на все множество возможных реализаций сигнала и потому опирались на предельные значения его динамических характеристик, то при адаптивной дискретизации мы ориентируемся на динамические характеристики конкретной реализации, что позволяет получить минимальное число выборок, обеспечивающих восстановление этой реализации с заданной точностью
В основе принципа адаптивной дискретизации лежит непосредственное слежение за текущей погрешностью восстановления сигнала ε
Наиболее широкое применение на практике получили алгоритмы дискретизации с адаптацией по длине интервала аппроксимации. В процессе последовательного наращивания интервала аппроксимации производится сравнение сигнала u(t) с воспроизводящей функцией u*(t), формируемой с учетом текущих значений динамических характеристик сигнала. Когда погрешность воcпроизведения достигает заданного значения ε0, наращивание интервала прекращается и производится отсчет. Интервалы времени между отсчетами при этом оказываются произвольными.
В качестве воспроизводящих функций наиболее часто используются степенные алгебраические полиномы (2.5) нулевой и первой степеней. При этом возможны как интерполяционные, так и экстраполяционные способы адаптивной дискретизации Интерполяционные способы не нашли широкого применения, поскольку их реализация связана с запоминанием сигнала на интервале аппроксимации и выполнением большого числа вычислительных операций. Поэтому ограничимся рассмотрением примеров адаптивной дискретизации на основе экстраполяции
Пример 2.6. Провести адаптивную дискретизацию реализации сигнала u(t), изображенной на рис 2.11, с использованием аппроксимирующего многочлена типа (2.5) нулевой степени. Наибольшее допустимое отклонение равно e0.
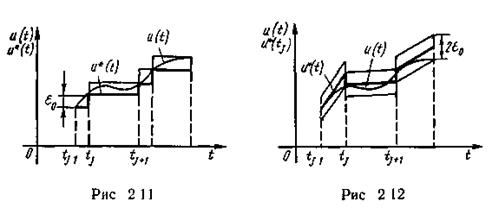
На момент tj начала каждого интервала аппроксимирующий полином u*(t) принимаем равным u(tj) и вычисляем разность Δu(t)=u(t) - u*(tj), которую сравниваем с ε0. Установление равенства
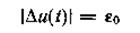
соответствует моменту tj+1 окончания интервала и проведения очередного отсчета.
Результаты дискретизации отображены на том же рисунке.
Пример 2.7.Провести адаптивную дискретизацию реализации сигнала u(t) изображенного на рис 2.12 многочленом типа (2.5) первой степени. Наибольшее допустимое отклонение равно ε0.
На момент tj начала каждого интервала аппроксимации
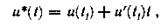
где u'(tj) — производная сигнала u(t) в момент времени tj.
