Отношение правдоподобия. Правило решения

Рассмотрим постановку задачи оптимального обнаружения реальных сигналов, которые являются функциями времени. Напомним, что пространственные и поляризационные характеристики сигналов и помех пока не рассматриваются, всё взимание сосредоточено только на их временных характеристиках.

Принятый сигнал f(t) может состоять из сигнала m(t) и помехи n(t)

f(t) = m(t) + n(t) → - условие A₁ ,

либо сводиться только к помехе

f(t) = n(t) → - условие А₀ .

Задача заключается в том, чтобы указать правило решения, которое бы "наилучшим" образом позволило на основании принятого сигнала f(t) решить, какое из двух условий (A₁ или A₀) верно.

Пусть принятый сигнал f(t) характеризуется плотностью вероятности p₁(f) при условии A₁ и плотностью вероятности p₀(f) при условии А₀. Если вместо непрерывной функции f(t) рассматривать L дискретных значений f₁ , f₂ ,..., f_L то функции p₁(f) и p₀(f) являются 2L - мерными распределениями вероятностей, что более подробно следует записать так:

,

.

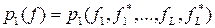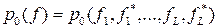Вероятности попадания реализации f(t) на "дорожку", определяемую

интервалами:

,

,

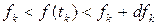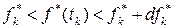при условиях A₁ и A₀ равны:

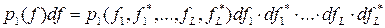
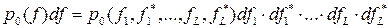
С позиций более общей интерпретации каждая входная реализация f(t) представляется точкой в 2L - мерном пространстве с координатами, причём 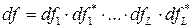есть элемент объёма в этом пространстве, а p₁(f)df и p₀(f)df есть вероятности попадания входной реализации в этот элемент объёма при наличии и отсутствии полезного сигнала.

Выбор правила решения заключается в разбиении 2L - мерного пространства 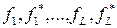на такие две области Г₁ и Г₀ , когда при попадании точки в область Г₁ выносится решение о верности условия A₁, а при попадании в область Г₀ - решение о верности условия A₀. Подобное разбиение схематически изображено на рис. 2.1 для случая 2L =2 .

Учитывая введенные определения и обозначения, получаем соотношения

для вероятностей правильного обнаружения и ложной тревоги:

, ,

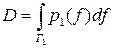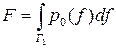а также для среднего риска

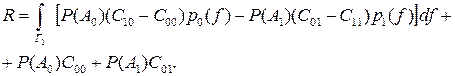
Рис. 2.1. Схематическое разбитие двумерного пространства решения на области Г₁ и Г₀.

Слагаемые, находящиеся вне интеграла, от правила решения (от областей Г₁ и Г₀) не зависят, поэтому минимум среднего риска достигается при минимуме интеграла. Первое слагаемое в подынтегральном выражении положительно, а второе - отрицательно, т.к. C₁₀ - C₀₀ > 0 ,C₀₁ - C₁₁ > 0.

Если выбрать область Г₁ так, чтобы выполнялось условие

Р(А₁) · (C₀₁ - C₁₁) · p₁(f) > Р(А₀) · (C₁₀ - C₀₀) · p₀(f)

или

,

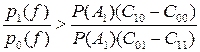то величина R будет минимальна. Действительно, исключение из области Г₁ любой части, в которой выполняется это неравенство, приводит к увеличению интеграла и среднего риска. Наоборот, включение в область Г₁ любого элемента объёма, в котором справедливо противоположное неравенство, также ведёт к увеличению среднего риска.

Отношение

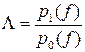
называется отношением правдоподобия.

Величину

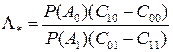
можно рассматривать как некоторый порог.

Используя введённые определения, можно сформулировать правило решения в, следующем виде (так называемое байесово правило выбора решений): для принятия решения о наличии или отсутствии полезного сигнала (объекта наблюдения) надо вычислить отношение правдоподобия Λ принятого сигнала f(t) и сравнить его с порогом Λ_*:

если Λ ≥ Λ_* то принимается решение А^*₁,

если Λ < Λ_* то принимается решение А^*₀ .

Отношение правдоподобия (или любая монотонная функция его) является отражением структуры оптимальной системы обработки принятого сигнала в структуре, оптимального обнаружителя (рис. 2.2).

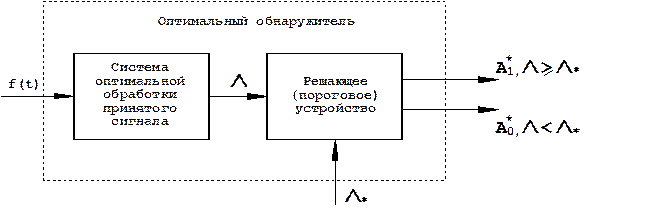Рис. 2.2. Структура оптимального обнаружителя.

Отношение правдоподобия представляет собой математическое олицетворение физического устройства, применяемого для обработки принятого сигнала. Одной из главных задач синтеза системы обнаружения является определение облика системы оптимальной обработки принятого сигнала, т.е. интерпретация математических операций, содержащихся в выражении отношения правдоподобия (усиление, задержка, умножение, сложение, вычитание, интегрирование, дифференцирование, возведение в степень), при помощи физически реализуемых аналоговых, цифровых или оптических элементов.

Выработка решения сводится лишь к испытанию на порог напряжения на выходе системы обработки принятого сигнала.

Выбор порога решения

Различают различные критерии выбора порога решения. Остановимся на двух из них.

Критерий идеального наблюдателя.

Под "идеальностью" наблюдателя подразумевается "бескорыстность выполнения задачи - стоимость правильных решений принимается равной нулю, т.е. наблюдатель не вознаграждается за принятые правильные решения:

С₀₀ = С₁₁ = 0,

а также одинаковая "нетерпимость" к ошибочным решениям - стоимость пропуска цели и ложной, тревоги одинаково высоки:

С₀₁ =С₁₀ = 1.

При этом средний риск равен суммарной вероятности ошибки

,

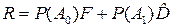а порог определяется только априорными вероятностями наличия или отсутствия сигнала (объекта наблюдения).

.

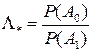Критерий Неймана-Пирсона.

Согласно этому критерию порог выбирают исходя из требуемой фиксированной вероятности ложной тревоги Λ_* → F = const.

При этом выбор пространства решения Г₁ должен минимизировать вероятность пропуска 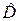или максимизировать вероятность правильного обнаружения D. Нейман и Пирсон показали, что в этом случае сохраняется правило решения байесового типа:

если 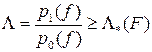, то А^*₁.

Таким образом, если «идеальный наблюдатель» исходит из минимизаций полной вероятности ошибки, то «наблюдатель Неймана-Пирсона» исходит из минимизации только вероятности пропуска сигнала при фиксированной вероятности ложной тревоги. И система Неймана-Пирсона, и система идеального наблюдателя принадлежат к байесову классу систем, связанных с испытанием на порог отношения правдоподобия и минимизирующих средний риск.