Набор заданий для выполнения расчетно-графической работы
Теоретические вопросы
1) Понятие первообразной функции. Теоремы о первообразных.
2) Неопределенный интеграл, его свойства.
3) Таблица неопределенных интегралов.
4) Замена переменной и интегрирование по частям и неопределенном интеграле.
5) Разложение дробной рациональной функции на простейшие дроби.
6) Интегрирование простейших дробей. Интегрирование рациональных функций.
7) Интегрирование выражений, содержащих тригонометрические функции.
8) Интегрирование иррациональных выражений.
9) Понятие определенного интеграла, его геометрический смысл.
10) Основные свойства определенного интеграла.
11) Теорема о среднем.
12) Производная определенного интеграла по верхнему пределу. Формула Ньютона-Лейбница.
13) Замена переменной и интегрирование по частям в определенном интеграле.
14) Интегрирование биномиальных дифференциалов.
15) Вычисление площадей плоских фигур.
16) 16) Определение и вычисление длины кривой, дифференциал длины дуги кривой.
Теоретические упражнения
1) Считая, что функция  равна 1 при
равна 1 при  , доказать,
, доказать,
что она интегрируема на отрезке  .
.
2) Какой из интегралов больше:
 или
или  ?
?
3) Пусть  — непрерывная функция, а функции
— непрерывная функция, а функции  и
и  дифференцируемые. Доказать, что
дифференцируемые. Доказать, что

4) Найти 
5) Найти точки экстремума функции


6) Пусть 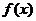 — непрерывная периодическая функция с периодом
— непрерывная периодическая функция с периодом  . Доказать, что
. Доказать, что

 .
.
7) Доказать, что если 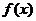 — четная функция, то
— четная функция, то

8) Доказать, что для нечетной функции 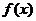 справедливы равенства
справедливы равенства
 и
и 
Чему равен интеграл  ?
?
9) При каком условии, связывающем коэффициенты а, b, с, интеграл  является рациональной функцией?
является рациональной функцией?
10) При каких целых значениях n интеграл  выражается элементарными функциями?
выражается элементарными функциями?
Расчетные задания
Задача 1.Найти неопределенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 2.Вычислить определенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 3.Найти неопределенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 4.Вычислить определенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 5.Найти неопределенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 6.Найти неопределенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 7.Найти неопределенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 8.Вычислить определенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 9.Вычислить определенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 10.Вычислить определенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 11.Вычислить определенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 12.Вычислить определенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 13.Найти неопределенные интегралы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 14.Вычислить площади фигур, ограниченных графиками функций.
1. 
2. 
3. 
4. 
5.  6.
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 15.Вычислить площади фигур, ограниченных линиями, заданными уравнениями.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 16.Вычислить площади фигур, ограниченных линиями, заданными уравнениями в полярных координатах.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 17.Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 18.Вычислить длины дуг кривых, заданных параметрическими уравнениями.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
Задача 19.Вычислить длины дуг кривых, заданных уравнениями в полярных координатах.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16.
