Скалярный потенциал магнитного поля

Для совокупности точек, где d = 0, rot Н == 0, магнитное поле можно рассматривать как потенциальное, т. е. как поле, каждая точка которого имеет скалярный магнитный потенциал j_m. Следовательно, для таких областей можно принять

H = - grad j_м. (13.10)

Так как div В = div m_a Н = 0, то при m_a = const div Н = 0.

Подставив в последнее выражение-grad j_м, вместо Н, получим

div grad j_м = 0.

Таким образом, скалярный потенциал магнитного поля j_м, о котором может идти речь только для областей, не занятых током, подчиняется уравнению Лапласа:

Ѳj_м=0. (13.11)

Разность скалярных магнитных потенциалов между точками 1 и 2 называют падением магнитного напряжения между точками 1 и 2

U_м12 = j_м1 - j_м2 = .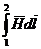

Падение магнитного напряжения между точками 1 и 2 по какому-то одному пути (например, по пути 132, рис. 13.5, а) равно падению магнитного напряжения между теми же точками по какому-то другому

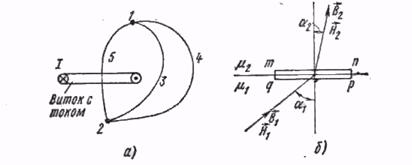
Рис.13.5 Падение магнитного напряжения между точками 1 и 2 может иметь разные значения в зависимости от пути интегрирования.

Пути (например, по пути 142) в том случае, когда эти пути образуют замкнутый контур, ток внутри которого равен нулю. Если же замкнутый контур, образованный двумя путями, охватывает некоторый ток, то падение магнитного напряжения по первому пути не равно падению магнитного напряжения по второму пути — они будут различаться на величину тока, охваченного контуром. Последнее вытекает из закона полного тока.

Так, применительно к рис. 13.5,а 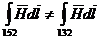(ибо из закона полного тока следует, что 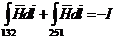,или 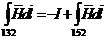). Следовательно, для того чтобы разность магнитных потенциалов между двумя точками магнитного поля не зависела от пути, надо наложить запрет на прохождение через контур (виток) с током, мысленно натянув на этот контур некоторую пленку. При прохождении через эту пленку j_м изменяется скачком на величину тока в контуре.

Следует различать понятия «падение магнитного напряжения» и «магнитное напряжение». Первое определяется только линейным интегралом от Н на dl по выбранному пути. Второе — не только этим интегралом, но и м.д.с., имеющейся на пути. Здесь имеется полная аналогия с понятиями «падение напряжения» и «напряжение» в электрической цепи.

Граничные условия

Подобно тому, как в электростатическом поле и в поле проводящей среды выполнялись определенные граничные условия, в магнитном поле также имеют место аналогичные условия:

Н_1t =Н_2t, (13.12)

В_1n =В_2n (13.13)

Условие (13.12) означает, что на границе раздела двух однородных и изотропных сред, различных в магнитном отношении (различные m), равны тангенциальные составляющие векторов напряженности магнитного поля. Условие (13.13) свидетельствует о равенстве нормальных составляющих векторов магнитных индукций на границе раздела. Условие (13.12) выводят путем составления линейного интеграла 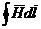по плоскому контуру mnpq (рис. 13.5, б) и приравнивания его нулю (так как он не охватывает тока). Стороны nр и qm ничтожно малы по сравнению со сторонами mn и pq. Длину стороны mn и равную ей по величине длину стороны pq обозначим через dl. Тогда H₁sina₁dl — Н₂sina₂dl = 0, но H₁sina₁ = Н_1t, H₂sina₂ = Н_2t, следовательно Н_1t = Н_2t.

Условие (13.12) не выполняется, если на поверхности раздела двух сред протекает так называемый поверхностный ток. Под ним понимают ток, протекающий по бесконечно тонкому плоскому проводнику, помещенному на границе раздела. В этом случае 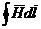будет равняться не нулю, а поверхностному току sdl, который оказался внутри замкнутого контура:

H₁sina₁dl — Н₂sina₂dl = sdl и в силу этого H_1t — Н_2t = s.

Другими словами, при наличии поверхностного тока с плотностью s тангенциальная составляющая напряженности поля терпит разрыв. Как правило, поверхностный ток отсутствует, и условие (13.12) выполняется. Равенство нормальных составляющих векторов магнитной индукции следует из принципа непрерывности магнитного потока:

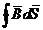= 0.

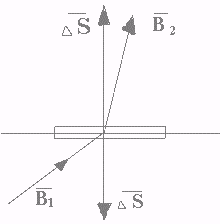
Для того чтобы убедиться в справедливости (13.13), на границе раздела выделим небольшой плоский параллелепипед и подсчитаем потоки вектора Вчерез нижнюю грань (рис. 13.6) —B_1nDS и верхнюю B_2nDS. Сумма потоков равна нулю: —В_1nDS + B_2nDS = 0. Следовательно, B_1n = B_2n.

Из (13.12) и (13.13) вытекает соотношение

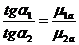. (13.14)

Рис.13.6. Граничные условия на границе раздела двух тел с различными магнитными проницаемостями.

Оно дает связь между углом падения a₁ и углом преломления a₂ (рис. 13.5, б). Если магнитные силовые линии выходят из среды с большой магнитной проницаемостью, например m_1a = 10⁴ m₀, в среду с малой магнитной проницаемостью, например в воздух m_2a = m₀, то

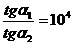и tga₁ = 10^-4 tga₂.

Следовательно, угол a₂ много меньше угла a₁.

Например. Найти угол a₂, под которым силовые линии выходят в среду с магнитной проницаемостью m_2a, если угол a₁ = 89°;

m_1a = 10⁴ m₀, m_2a = m₀.

Решение. tga₁ = tg 89°= 57,29;

tga₂ = 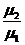tga₁ = 10^-4 tga₁ = 0,005729; a₂ = 20'.