Гармонические механические колебания
1) Кинематическое уравнение гармонических колебаний материальной точки
x = Acos(wt + j),
где x – смещение от положения равновесия; A – амплитуда колебаний; (wt+ j) – фаза; j – начальная фаза; w – круговая частота.
2) Скорость и ускорение материальной точки, совершающей гармонические колебания
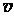 = - A wsin(wt + j),
= - A wsin(wt + j),
a = - A w2cos(wt + j).
3) Период колебаний
а) тела, подвешенного на пружине,
T = 2p 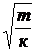 ,
,
где m – масса тела; к– жесткость пружины;
b) математического маятника
T = 2p 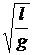 ,
,
где l– длина маятника; g– ускорение свободного падения;
c) физического маятника
T = 2p 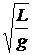 = 2p
= 2p 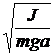 ,
,
где J – момент инерции колеблющегося тела относительно оси колебаний; а – расстояние от центра тяжести маятника до оси колебаний; L = J/ma – приведенная длина физического маятника.
Примеры решения задач
Задача 1
К невесомой пружине, коэффициент упругости которой 200 Н/м, прикреплен груз массой 1 кг. Груз смещен на 10 см от положения равновесия, после чего предоставлен себе. Определить наибольшее и наименьшее ускорения груза. Трением пренебречь.
| Дано: k = 200 Н/м m = 1 кг А0 = 10 см = 0,1 м | Решение: Под действием силы упругости груз совершает свободные гармонические колебания, уравнение которых запишем в виде 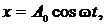 (1) (1) |
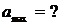 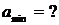  |
где 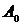 – амплитуда колебания;w– циклическая частота.
– амплитуда колебания;w– циклическая частота.
Продифференцировав выражение (1) по времени, определим скорость груза:
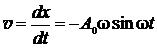 , (2) а после дифференцирования скорости по времени – ускорение
, (2) а после дифференцирования скорости по времени – ускорение
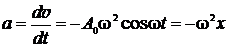 . (3)
. (3)
Так как 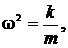 то ускорение а можно записать в виде
то ускорение а можно записать в виде
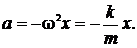 (4)
(4)
Ускорение имеет максимальное значение при 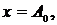 то есть при наибольшем отклонении от положения равновесия
то есть при наибольшем отклонении от положения равновесия
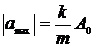 . (5)
. (5)
В положении равновесия, при x = 0, ускорение a = 0. Подставляя числовые значения в выражение (5), получим:
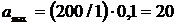 м/с2.
м/с2.
5.2.2. Затухающие колебания
1) Уравнение затухающих колебаний
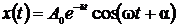 ,
,
где 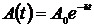 – амплитуда затухающих колебаний;
– амплитуда затухающих колебаний; 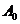 – начальная амплитуда (приt = 0);
– начальная амплитуда (приt = 0); 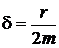 – коэффициент затухания;
– коэффициент затухания; 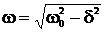 – круговая частота.
– круговая частота.
2) Логарифмический декремент затухания
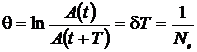 ,
,
где T – период колебаний; 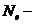 количество колебаний, совершаемых за время уменьшения амплитуды в e раз.
количество колебаний, совершаемых за время уменьшения амплитуды в e раз.
3) Добротность колебательной системыпри 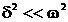 :
:
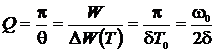 ,
,
где 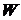 – полная энергия системы;
– полная энергия системы; 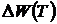 – потери энергии за период.
– потери энергии за период.
Примеры решения задач
Задача1
Прибор для измерения плотности жидкостей – ареометр массой 0,8 кг с цилиндрической трубкой диаметром 0,3 см опущен в жидкость плотностью 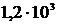 кг/м3. Ареометр получил небольшой импульс в вертикальном направлении и опустился на глубину
кг/м3. Ареометр получил небольшой импульс в вертикальном направлении и опустился на глубину 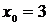 см. Коэффициент сопротивления
см. Коэффициент сопротивления 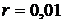 кг/с. Определить: циклическую частоту колебаний; количество колебаний, через которое амплитуда уменьшится в 3 раза.
кг/с. Определить: циклическую частоту колебаний; количество колебаний, через которое амплитуда уменьшится в 3 раза.
Дано: m = 0,08 кг d = 0,3 см = 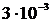 м м 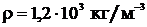 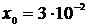 м м 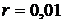 кг/с кг/с | Решение: При опускании ареометра в жидкость появляется квазиупругая выталкивающая сила 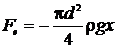 и сила сопротивления и сила сопротивления 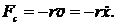 Уравнение движения ареометра Уравнение движения ареометра |
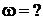 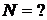  |
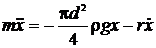
преобразуется в уравнение колебаний
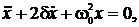
где 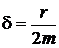 – коэффициент затухания;
– коэффициент затухания; 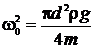 – собственная частота колебаний.
– собственная частота колебаний.
Частота затухающих колебаний
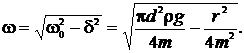
Подставляя числовые значения, получим: 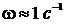
Амплитуда затухающих колебаний
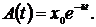
При уменьшении амплитуды в 3 раза
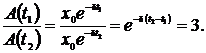
Отсюда 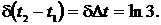
Учитывая, что 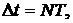 а
а 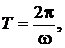 получим:
получим:
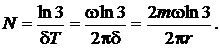
Подставляя числовые значения, получим: 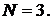
5.2.3. Электромагнтные колебания
1) Эффективные (действующие) значения напряжения и силы переменного тока
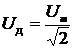 ,
, 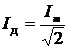 ,
,
где Um иIm – амплитудные значения напряжения и силы тока.
2) Закон Ома для цепи переменного тока, содержащей последовательно соединенные резистор сопротивлением R, катушку индуктивностью L и конденсатор электроемкостью С
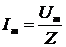 или
или 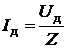 ,
,
где Z = 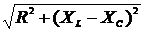 – полное сопротивление цепи;
– полное сопротивление цепи; 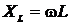 – индуктивное сопротивление;
– индуктивное сопротивление; 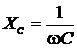 – емкостное сопротивление;
– емкостное сопротивление; 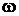 – круговая частота переменного тока.
– круговая частота переменного тока.
При этом сдвиг фаз между напряжением и силой тока определяется из условия
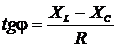 или
или 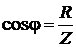 .
.
3) Средняя мощность, выделяемая в цепи переменного тока,
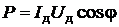 ,
,
где j – сдвиг фаз между напряжением и силой тока.
4) Период собственных электромагнитных колебаний в контуре без активного сопротивления (формула Томсона)
T = 2 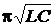 ,
,
где L– индуктивность контура; С – электроемкость.
Примеры решения задач
Задача 1.
Разность потенциалов между обкладками конденсатора электроемкостью 0,5 мкФ в колебательном контуре изменяется со временем по закону U = 100sin1000pt B. Определить период собственных колебаний, индуктивность, полную энергию контура и максимальную силу тока, текущего по катушке индуктивности. Активным сопротивлением контура пренебречь.
Дано: 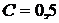 мкФ = мкФ = 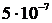 Ф Um = 100 B Ф Um = 100 B 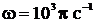 | Решение: Напряжение на конденсаторе изменяется по гармоническому закону U = Umsinwt, гдеUm – амплитудное (максимальное) значение |
Т = ? 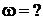 Im = ? L = ? Im = ? L = ? |
напряжения на обкладках конденсатора; w – собственная круговая частота колебаний, которая связана с периодом соотношением T=2p/w. Отсюда находим
Т = 2π/1000π = 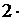 10-3 с.
10-3 с.
Период собственных колебаний в контуре определяется по формуле Томсона T = 2p 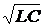 , откуда
, откуда
L = 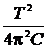 ;L =
;L = 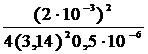 = 0,2 Гн.
= 0,2 Гн.
Полная энергия контура складывается из энергии электрического поля WC конденсатора и энергии магнитного поля WL катушки:
W = WC+WL= 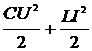 .
.
Полная энергия электрического контура равна максимальной энергии поля конденсатора WCmax= 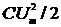 или максимальной энергии поля катушки WLmax =
или максимальной энергии поля катушки WLmax = 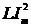 /2.
/2.
Таким образом,
 |  |
W =
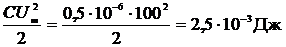 .
.  |
Зная полную энергию, можно определить максимальную силу тока, протекающего по катушке индуктивности:
 |
Im=
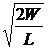 ; Im =
; Im = 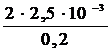 = 0,16 A.
= 0,16 A. 5.2.4. Сложение гармонических колебаний
1) Сложение гармонических колебаний одного направления и одинаковой частоты:
- амплитуда результирующего колебания
A = 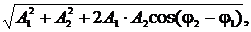
- начальная фаза результирующего колебания
j= arctg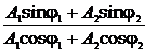 .
.
2) Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях ( 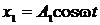 , y =
, y = 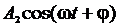 ):
):
а) 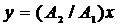
 (если разность фаз
(если разность фаз 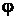 = 0);
= 0);
б) 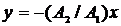 (если разность фаз
(если разность фаз 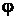 =
= 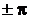 );
);
в) 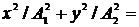 1(если разность фаз
1(если разность фаз 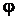 =
= 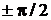 ).
).
Примеры решения задач
Задача1
Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых:
x= A1cos 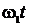 ,(1)
,(1)
y = A2cos 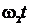 , (2)
, (2)
где А1 = 1 см; 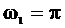 с-1; А2 = 2 см;
с-1; А2 = 2 см; 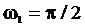 с-1.
с-1.
Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.
Дано: x = A1cos 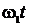 y = A2cos y = A2cos 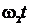 А1 = 1 см = 0,01м А2 = 2 см = 0,02м А1 = 1 см = 0,01м А2 = 2 см = 0,02м | Решение: Чтобы определить траекторию точки, исключим время из уравнений (1) и (2). Заметив, что y = A2cos(w1/2)t , применим формулу косинуса половинного угла: 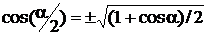 . . |
| y = f(x) = ? |
Используя это соотношение и отбросив размерности x и y,можно написать:
y= 2 cos 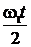 = 2
= 2 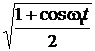 ; х = cos
; х = cos 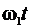 ,
,
откуда
y = 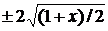 или y =
или y = 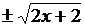 . (3)
. (3)
Выражение (3) есть уравнение параболы, ось которой совпадает с осью ОХ. Как показывают уравнения (1) и (2), амплитуда колебаний точки по оси OX равна 1, а по оси ОУ –2. Следовательно, абсциссы всех точек траектории заключены в пределах от –1 до +1, а ординаты – от –2 до+2.
Для построения траектории найдем из уравнения (3) значения y, соответствующие ряду значений x, удовлетворяющих условию 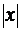
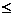 1:
1:
 |
x y = 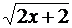 х y =
х y = 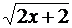
 |
- 1 0 0 ± 1,41
- 0,75 ± 0,71 0,5 ± 1,73
- 0,5 ± 1  1 ± 2
1 ± 2
1 x
-1
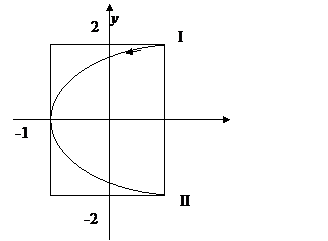
Рис. 1
Начертив координатные оси и выбрав единицу длины (сантиметр), построим точки. Соединив их плавной кривой, получим траекторию результирующего колебания точки, которая представляет собой часть параболы, заключенной внутри прямоугольника амплитуд.
Далее определим направление движения точки. Из уравнений (1) и (2) находим, что период колебаний точки по горизонтальной оси Тх = 2с, а по вертикальной оси Ту = 4 с.
Следовательно, когда точка совершает одно полное колебание по оси ОХ, она совершает только половину полного колебания по оси OУ. В начальный момент (t = 0) имеем: х = 1, у = 2 (точка находится в положении 1) при t = 1 с получим: х = –1 и у = 0 (точка находится в вершине параболы); При t = 2 с получим: х = 1 и у = –2 (точка находится в положении 2). После этого она будет двигаться в обратном направлении.
