Вычисление двойного интеграла в полярных координатах

Для упрощения вычисления двойного интеграла часто применяют метод подстановки, т.е. вводят новые переменные под знаком двойного интеграла.

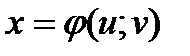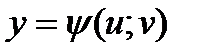Введём новые переменные , пусть и , функции φ и ψ имеют в некоторой области плоскости Оuv непрерывные частные производные.

Функциональный определитель

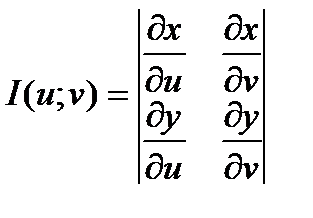- называется определителем Якоби или якобианом.

Если функция 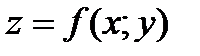непрерывна в области D, а якобиан 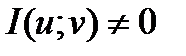, то справедлива формула замены переменных в двойном интеграле

.

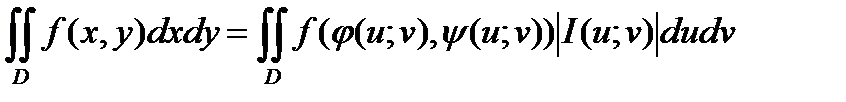Рассмотрим частный случай: замену декартовых координат х и уполярными координатами r и φ. Прямоугольные и полярные координаты связаны формулами

.

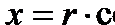
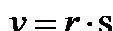В качестве u и v возьмём полярные координаты r и φ. Составим Якобиан преобразования u=r, v=φ.

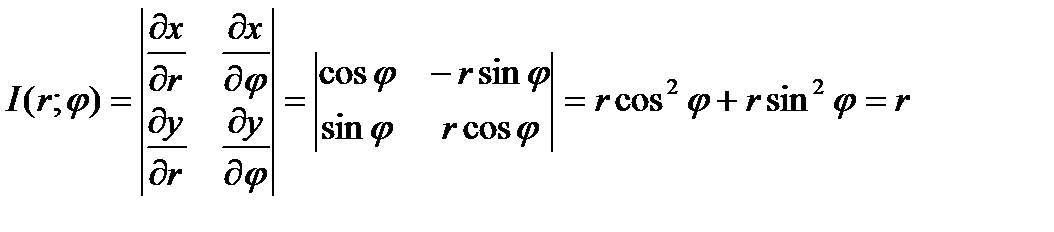
Формула замены переменных x, y в полярных координатах будет иметь вид

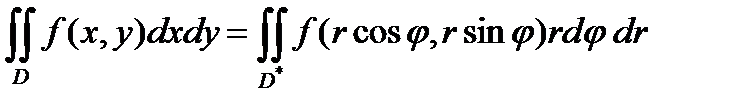
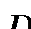- область в полярной системе координат, соответствует области D в декартовой системе координат.

Для вычисления двойного интеграла в полярных координатах применяют тоже правило сведения его к двукратному интегралу

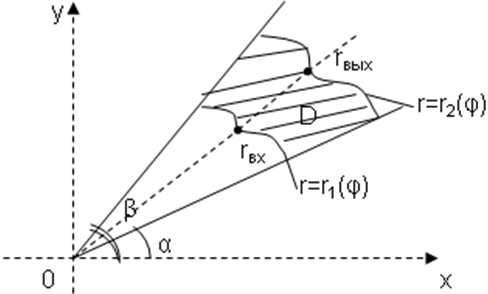
Рис. 9

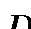Если область (рис.9) ограниченна лучами φ=α и φ=β , где α<β и кривыми 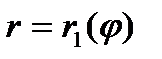, , 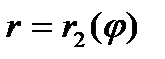где 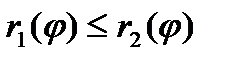, для любого 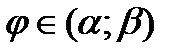, т.е. область 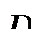-правильная: то двойной интеграл в полярной системе координат вычисляется по следующей формуле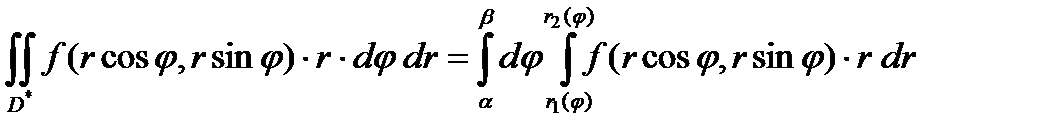

Внутренний интеграл берётся при условии, что φ - константа.

Пусть функции 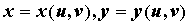взаимно однозначно отображают открытое множество, содержащее область 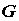плоскости 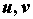на открытое множество, содержащее область 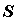, и пусть 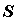является образом 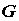. Если 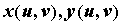и их частные производные непрерывны, а определитель 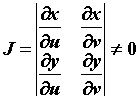, то 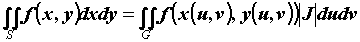. Выражение 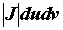называется элементом площади в криволинейных координатах, функциональный определитель 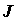- якобианом.

Якобиан, функциональный определитель ½a_ik½₁ⁿ с элементами 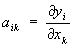, где y_i = f_i(X₁,...,X_n), l £ i £ n, — функции, имеющие непрерывные частные производные в некоторой области А; обозначение:

.

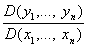Введён К. Якоби (1833, 1841). Если, например, n = 2, то система функций

y₁ = f₁ (. x₁, x₂), y₂ = f₂(x₁, x₂) (1)

задаёт отображение области D, лежащей на плоскости x₁, x₂, на часть плоскости y₁, y₂. Роль Якобиан для этого отображения во многом аналогична роли производной для функции одной переменной. Например, абсолютное значение Якобиан в некоторой точке М равно коэффициенту искажения площадей в этой точке (т. е. пределу отношения площади образа окрестности точки М к площади самой окрестности, когда размеры окрестности стремятся к нулю). Якобиан в точке М положителен, если отображение (1) не меняет ориентации в окрестности точки М, и отрицателен в противоположном случае. Если Якобиан не обращается в нуль в области D и j (y₁, у₂) — функция, заданная в области D₁ (образе D), то

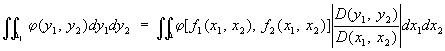
(формула замены переменных в двойном интеграле). Аналогичная формула имеет место для кратных интегралов. Если Якобиан отображения (1) не обращается в нуль в области Д, то существует обратное отображение

x₁ = j₁(y₁, y₂), x₁ = j₂(y₁, y₂),

причём

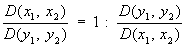
(аналог формулы дифференцирования обратной функции). Это утверждение находит многочисленные применения в теории неявных функций. Для возможности явного выражения в окрестности точки М (x₁⁽⁰⁾,..., x_n⁽⁰, y₁⁽⁰⁾,..., y_m⁽⁰⁾) функций y₁,..., у_т, неявно заданных уравнениями F_k (x₁,..., x_n, y₁,..., у_м) = 0, (2)

1 £ k £ m,

достаточно, чтобы координаты точки М удовлетворяли уравнениям (2), функции Fk имели непрерывные частные производные и Якобиан

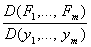
был отличен от нуля в точке М.

1. Применение двойного интеграла: вычисление геометрических величин – площади области, объема тела, площади поверхности тела.

2. Применение двойного интеграла: вычисление физических величин – массы пластины, моментов инерции плоской материальной пластины, координат центра тяжести материальной пластины, статических моментов пластины.

30. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрических и сферических координатах.