Множество U, содержащее в себе все элементы рассматриваемых множеств, называется универсальным множеством.

Множество A есть бесконечное множество, если оно имеет ту же мощность, что и хотя бы одно из его собственных подмножеств; в противном случае A – конечное множество.

Множества, равномощные множеству натуральных чисел N, называются счетными. Каждое бесконечное подмножество счетного множества счетное. Объединение счетного множества счетных множеств есть счетное множество.

Для описания множеств будем использовать два способа:

1. Перечисление: A = ía, b, cý; X = íx₁, x₂, ¼, x_ný.

2. Задание множества с помощьюзаписи свойства, определяющего отношение принадлежности элементов данному множеству:

A = íx: Q(x)ý - множеству А принадлежат все те и только те элементы х, которые обладают свойством Q(x).

Диаграммы Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри него - кругов (или каких-либо других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств.

Рис. 5. Универсальное множество на диаграмме Венна

Элементарные операции над множествами

Элементарных операций над множествами всего четыре:

пересечение, объединение, разность (дополнение), симметрическая разность.­­­­­

При этом первые три в большой степени аналогичны операциям (функциям) математической логики (алгебры логики) – конъюнкция (&), дизъюнкция (v), инверсия (ù ). Последняя четвертая операция является производной от первых трех.

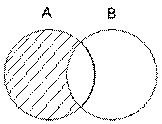
Итак, пересечение множеств(рис. 1): А Ç В = {х : х Î А и х Î В}.

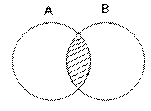Здесь символ «Ç» похож на русскую букву «П» («пересечение»), «и» – это логическая связка.

Рис. 1. Диаграмма Венна

Для пересечения множеств

Объединение множеств(рис. 2): А È В = {х : х Î А или х Î В}.

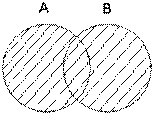«È» похоже на незавершенную русскую букву «О» («объединение»). ИЛИ здесь – не исключительное, т. е. это аналог «обычной» нестрогойдизъюнкции. Есть еще строгая дизъюнкция (ИЛИ-ИЛИ), в логике она обозначается « ».

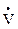Рис. 2. Объединение множеств

Утверждение: Для любых множеств А и В мощность объединения

çА 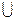Вç=çАç+çВç-çА 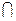Вç

Первые две операции фактически обладают теми же свойствами, что и операции &, v в алгебре логики.

Например, они коммутативны: А * В = В * А, и это, вообще-то, свойство логических связок «и», «или».

Они идемпотентны: А * А = А.

Свойство идемпотентности позволяет произвольно сжимать или расширять выражения, что весьма полезно в разного рода преобразованиях.

Кстати, {1, 2} Ç {2, 3} = {2},

{1, 2} È {2, 3} = {1, 2, 3},

но

{{1, 2}, {2, 3}} ¹ {1, 2 , 3}!

Разностьдвух множеств А \ В = {х : х Î А и х Ï В}. (рис. 3):

Рис. 3. Разность двух множеств

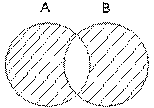Заштрихованная область на рис. 3 соответствует дополнению В до А. Аналогично можно определить разность В \ А, или дополнение А до В (область В на рис. 3 без общей части).

Симметрическая разность (рис. 4): А D В = (А È В) \ (А Ç В).

Рис. 4. Симметрическая разность

Как видно, здесь реализуется исключительное ИЛИ (строгая дизъюнкция). В алгебре логике существует аналог: А Å В = (А v В) .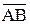

Действительно, (А v В) 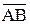= (А v В) (`А v `В ) = А`В v `АВ = А Å В.

Дополнение множества (до универсального): А¢ = Е \ А = {х : х Ï А}.

Множество и его дополнение однозначно определяются двумя равенствами (используются в доказательствах):

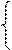А Ç А¢ = Æ,

А È А¢ = Е.