Различные уравнения плоскости в пространстве

Раздел 5. Аналитическая геометрия.

1. Различные уравнения плоскости в пространстве

2. Частные случаи общего уравнения плоскости

3. Взаимное расположение двух плоскостей

4. Расстояние от точки до плоскости

5. Различные уравнения прямой в пространстве

6. Взаимное расположение двух прямых в пространстве

7. Взаимное расположение прямой и плоскости в пространстве

8. Различные уравнения прямой линии на плоскости

9. Геометрическая задача линейного программирования

Различные уравнения плоскости в пространстве.

В предыдущих параграфах говорилось о том, что каждой точке пространства ставится в соответствие упорядоченный набор чисел – её координаты. Естественно предположить, что если точки, обнаруживая некоторую закономерность, «выстраиваются» в виде некоторой линии или поверхности, то и их координаты также будут демонстрировать эту закономерность, удовлетворяя, как правило, некоторому уравнению, которое и называется уравнением этой линии, или поверхности.

Рассмотрим сначала пространство R³ – реальное трёхмерное пространство (в котором мы живём). Простейшей поверхностью в пространстве является плоскость. Плоскость может быть задана различными способами, этим способам соответствуют различные формы уравнений этой плоскости. В частности, плоскость вполне

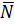определена, если известна какая-нибудь

M

точка М₀, лежащая на этой плоскости

(она называется опорной), и какой-нибудь

вектор, от которого требуется лишь одно

Рис.1 – он должен быть перпендикулярен

плоскости. Такой вектор называется вектором нормали и обычно обозначается 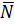(см. рис. 1).

Составить уравнение плоскости – значит охарактеризовать некоторым уравнением все точки плоскости. Для этого берём из этого бесчисленного множества точек любую (так сказать, представителя этого множества) и составляем для неё (т.е. для её координат) на основе замеченной закономерности уравнение. Поскольку точка была любой, то это уравнение будет справедливым и для всех точек плоскости.

Возьмём произвольную точку М (см. рис.1). Теперь образуем вектор 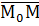. Ясно, что 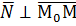. Воспользуемся условием перпендикулярности двух векторов – их скалярное произведение равно нулю:

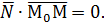(1)

Уравнение (1) называют векторным уравнением плоскости. Это уравнение справедливо в любой системе координат.

Рассмотрим теперь уравнение (1) в декартовой системе координат. Пусть точка М₀ имеет координаты 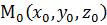, координаты вектора 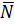принято обозначать: 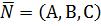. Т.к. точка М – произвольная, её координаты: 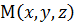, следовательно, 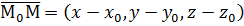. Тогда формула (1) примет вид

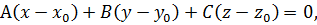(2)

его будем называть уравнением плоскости с опорной точкой и вектором нормали. Раскроем скобки в уравнении (2):

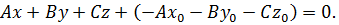Обозначив, 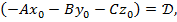получим

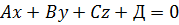(3)

Уравнение (3) называется общим уравнением плоскости. Отсюда видно, что всякое уравнение первой степени представляет собой плоскость.

Хорошо известно, что три точки однозначно определяют плоскость.

М1

М

М₂ Пусть точки М₁, М₂, М₃ образуют

некоторую плоскость (т.е. не лежат

М₃ на одной прямой). Составим

уравнение этой плоскости

Рис. 2 (см. рис.2). Для этого возьмём

произвольную точку М, лежащую в плоскости и рассмотрим три вектора 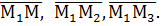Поскольку М принадлежит плоскости, векторы эти компланарны, а условием компланарности трёх векторов является равенство нулю их смешанного произведения:

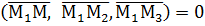(4)

Уравнение (4) – ещё одно векторное уравнение плоскости, справедливое для любой системы координат. В декартовой системе координат пусть 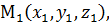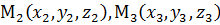, 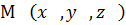; тогда

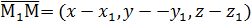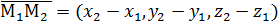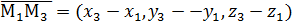, , и уравнение (4) выглядит следующим образом:

x – x₁ y – y₁ z – z₁

x₂ – x₁ y₂ – y₁ z₂ – z₁ = 0 (5)

x₃ – x₁ y₃ – y₁ z₃ – z₁

Уравнение (5) называют уравнением плоскости, проходящей через три точки.

Пример 1. Написать уравнение плоскости, проходящей через точку М₀(1,2,-3) перпендикулярно вектору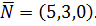

Решение. Воспользовавшись уравнением (2), получим уравнение плоскости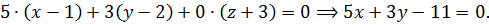

Заметим, что в уравнении могут отсутствовать некоторые переменные.

Пример 2. Написать уравнение плоскости, проходящей через начало координат перпендикулярно вектору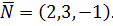

Решение. Воспользуемся уравнением (2): 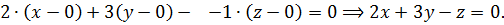Заметим, что в уравнении отсутствует свободный член (точнее, свободный член равен нулю).

Пример 3. Написать уравнение плоскости, проходящей через три точки А(1,1,3), В(0,2,3), С(1,5,7).

Решение. Воспользуемся уравнением (5):

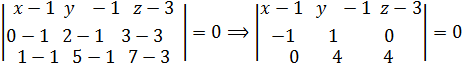
Вычислим определитель разложением по первой строке:

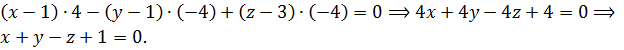
5.2. Частные случаи общего уравнения плоскости.

Возьмём общее уравнение плоскости 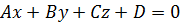и рассмотрим несколько его частных случаев.

1) D = 0, т.е. уравнение плоскости имеет вид

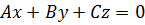(6)

Ясно, что этому уравнению всегда удовлетворяет точка О(0,0,0) – начало координат. Итак, если в уравнении плоскости свободный член равен нулю, то плоскость проходит через начало координат.

2) С = 0, т.е. уравнение плоскости имеет вид

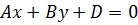(7)

Это означает, что вектор нормали имеет следующие координаты 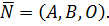Нетрудно увидеть, что 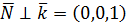- вектор нормали перпендикулярен базисному вектору 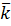, т.е. оси oz, т.к. их скалярное произведение равно нулю: 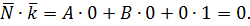Теперь понятно,

что плоскость параллельна оси oz (рис.3).

z

1

0 у

х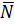

Рис.3

Аналогично, если В = 0, то плоскость параллельна оси ОУ; если А = 0, то плоскость параллельна оси ОХ.

Итак, если в уравнении плоскости равен нулю коэффициент при некотором неизвестном, то плоскость параллельна одноименной оси координат.

3)Пусть равны нулю два параметра – свободный член и один коэффициент, например, С = 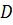= 0. Уравнение плоскости имеет вид

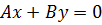(8)

Из предыдущего ясно, что С =0 означает, что плоскость параллельна оси oz, а 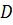= 0 означает, что плоскость проходит через начало координат. Объединяя оба замечания, получаем, что плоскость проходит через ось oz.

Общий вывод: если в уравнении равны нулю свободный член и коэффициент при каком-нибудь неизвестном, то плоскость проходит через соответствующую ось координат.

4) Пусть равны нулю два коэффициента при неизвестных, например А = В =0, т.е. уравнение плоскости имеет вид

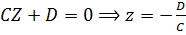. (9)

Учитываем предыдущие рассуждения: если А = 0, то плоскость параллельна оси ОХ; если В = 0, то плоскость параллельна оси ОУ, следовательно, если

А = В = 0, то плоскость параллельна осям ОХ и ОУ, т.е. перпендикулярна оси

z ОZ и отсекает на этой оси отрезок,

-D/С равный – D/С (см. рис.4).

0 у

х

Рис.4

Отсюда следует:

х = 0 – уравнение координатной плоскости yoz,

у = 0 – уравнение координатной плоскости хоz,

z = 0 – уравнение координатной плоскости уоz.

5.3. Взаимное расположение двух плоскостей.

Взаимное расположение двух плоскостей определяется с помощью угла между ними (см. рис.5. Вообще говоря, можно увидеть два угла,

которые плоскости образуют

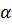между собой – угол и

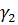
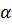
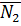дополнительный угол .

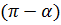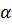Один из них – острый, другой

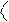
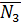тупой (в случае перпендикулярности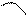

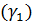
плоскостей оба угла совпадают).

Рис. 5

Под углом между двумя плоскостями понимается всегда острый угол 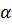. Этот угол вычисляется с помощью угла между векторами нормалей (через скалярное произведение векторов нормалей):

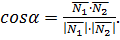(10)

На рис. 6 угол 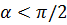. Однако, в качестве вектора нормали к плоскости 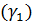можно взять вектор 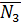. Тогда формула (10) даст косинус угла 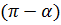. Косинусы углов 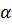и 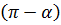будут отличаться лишь знаком. Поэтому, если мы хотим получить острый угол, то в формуле (10) скалярное произведение надо взять по абсолютной величине (по модулю):

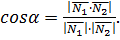(11)

Формулу (11) легко переписать в координатной форме. Пусть плоскости задаются уравнениям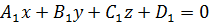и и 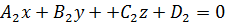. Таким образом, имеем два вектора нормале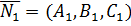й: и 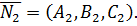По формуле (11) получим:

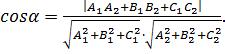(12)

Теперь нетрудно получить два крайних случая: перпендикулярность и параллельность плоскостей. Если плоскости перпендикулярны, то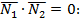

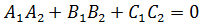- (13)

условие перпендикулярности плоскостей. Если плоскости параллельны, то векторы нормалей коллинеарны: 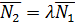, т.е. их координаты пропорциональны:

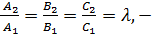(14)

условие параллельности плоскостей.

Пример 4. Даны три плоскости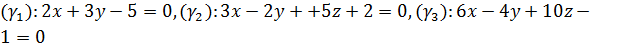

Найти углы между этими плоскостями.

Решение. Имеем три вектора нормалей 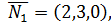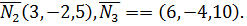Нетрудно заметить, что 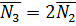, т.е. плоскости 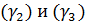параллельны. Найдём угол между плоскостями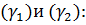

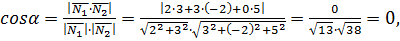т.е.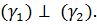

5.4. Расстояние от точки до плоскости.

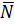
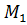
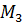Пусть требуется найти расстояние от

точки 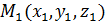до плоскости.

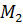Уравнение плоскости возьмём в виде

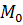уравнения с опорной точко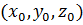й

и вектором нормали 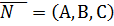, т.е.

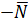Рис.5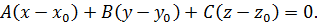

Как известно, расстояние равно длине перпендикуляра 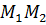(рис. 5). Для наглядности начало вектора 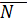поместим в точку 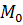. Построим прямоугольник 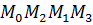и увидим, что 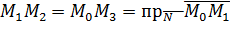- проекции вектора 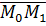на вектор нормали 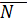(см. рис. 5).

Вспоминаем определение скалярного произведения векторов:

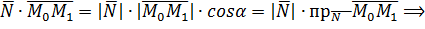
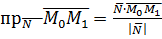(15)

Вновь замечаем, что на рис. 5 векторы 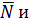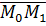образуют острый угол и потому 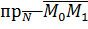является положительным числом. Если в качестве вектора нормали взять противоположный вектор (см. рис.5), то формула (15) даст отрицательное число, но расстояние есть число положительное, поэтому для расстояния d от точки 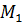до плоскости надо применять формулу

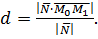(16)

Распишем формулу (16) в координатной форме:

.

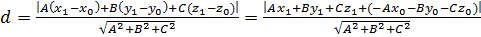Скобку 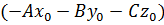мы ранее обозначали буквой D. Поэтому получаем формулу

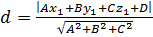, - (17)

для нахождения расстояния от точки 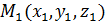до плоскости 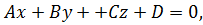заданной общим уравнением, надо в общее уравнение плоскости подставить координаты точки 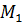, поделить на длину вектора нормали и взять по модулю.

Пример 5. Найти расстояние от точки 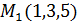до плоскости .

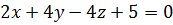Решение. Воспользуемся формулой (17):

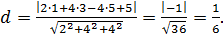
5.5. Различные уравнения прямой в пространстве.

Прямую линию в пространстве можно

задать с помощью опорной точки 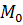, (т.е.

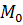М точка 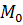лежит на прямой) и вектора 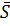, от

рис. 6 которого требуется одно – он должен

быть параллелен прямой. Такой вектор называется направляющим вектором прямой (см. рис. 6).

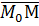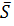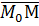Для составления уравнения возьмём произвольную точку М, принадлежащую прямой, - получим вектор . Векторы и . – коллинеарны (параллельны), следовательно имеет место соотношение

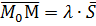, (18)

где 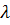- некоторое число. Уравнение (18) называется векторным уравнением прямой. Оно будет справедливо в любом пространстве и не зависит от выбора системы координат.

Рассмотрим теперь уравнение (18) в декартовой системе координат.

Обозначим соответствующие координаты: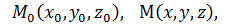

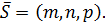Тогда уравнение (18) имеет вид: 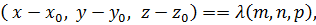или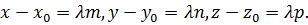

Это обычно записывают в следующих формах:

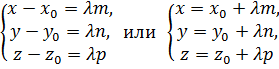(19)

Уравнения (19) называются параметрическими уравнениями прямой в пространстве ( 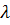- параметр).

Если из этих уравнений исключить параметр 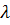, то получим:

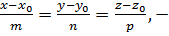(20)

это так называемые канонические уравнения прямой в пространстве. От канонических легко перейти к параметрическим уравнениям прямой – достаточно все уравнения (20) приравнять параметру .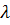

Важный для практики случай, когда прямая задаётся двумя точками 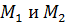, легко сводится к формуле (20), - стоит лишь заметить, что в качестве направляющего вектора можно взять вектор 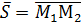, а опорной точкой можно считать любую из них. Пусть 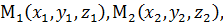тогда 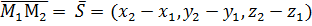и опорной точкой возьмём 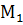, тогда из формулы (20) имеем:

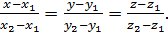(21)

Это уравнение называется уравнением прямой, проходящей через две точки.

5.6. Взаимное расположение двух прямых в пространстве.

Две прямые в пространстве могут

пересекаться, быть параллельными и

скрещивающимися.

Рис. 7

Пусть даны канонические уравнения двух прямых 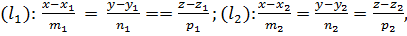т.е. с опорными точками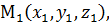 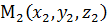и направляющими векторами = .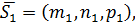

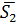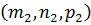Если 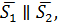т.е. 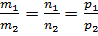, то прямые параллельны и даже могут совпадать. Подставим координаты опорной точки 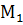в уравнение прямой 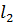(или наоборот). Если точка 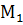лежит на прямой 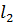, то прямые совпадают, в противном случае – параллельны.

Пусть теперь 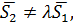т.е. векторы не параллельны (не коллинеарны). Тогда прямые могут пересекаться или скрещиваться. Как различить эти случаи? Делается это с помощью вектора 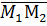(см. рис. 7). Ясно, что если прямые пересекаются, то векторы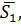 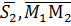находятся в одной плоскости (точнее, они параллельны одной плоскости – компланарны). Условием компланарности векторов является равенство нулю их смешанного произведения:

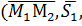
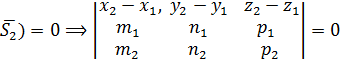(22)

Итак, если 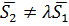и выполняется (22), то прямые пересекаются; в случае не выполнения равенства (22) прямые скрещиваются.

Заметим, что во всех рассмотренных случаях взаимного расположения прямых можно вычислять угол между прямыми. Угол 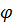между прямыми определяется с помощью скалярного произведения их направляющих векторов:

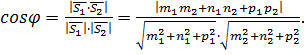(23)

Числитель взят по модулю для того, чтобы (как и для плоскостей) угол получался острым (в крайнем случае прямым).

Пример 6. Выяснить взаимное расположение трёх прямых:

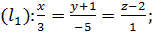
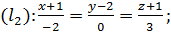
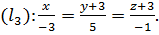
Решение. По данным уравнениям определяем опорные точки и направляющие векторы: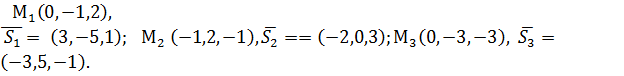

Легко заметить, что 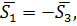следовательно, прямые 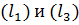или параллельны или совпадают. Подставим координаты точки 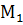в уравнение 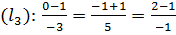- получили неверные равенства, следовательно, 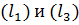параллельны.

Возьмём 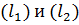и проверим условие (22):

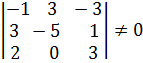, следовательно, 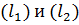скрещиваются.

Теперь проверим условие (22) для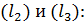

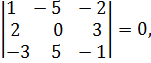следовательно, 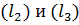пересекаются.

5.7. Взаимное расположение прямой и плоскости в пространстве.

Прямая и плоскость в пространстве могут пересекаться и тогда возникают вопросы нахождения угла между прямой и плоскостью и координатах точки их пересечения. Прямая и плоскость могут быть параллельными, в частном случае, прямая лежит в плоскости. Рассмотрим все эти случаи.

Угол 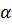между прямой и плоскостью (см. рис. 8) определяется с

помощью вектора 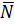нормали

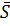
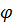плоскости и направляющего вектора

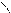
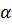
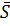прямой:

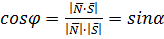(24)

Рис. 8

В формуле (24) скалярное произведение 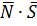взято по модулю, поскольку угол между прямой и плоскостью всегда острый (в крайнем случае прямой), а скалярное произведение может быть отрицательным.

Пусть 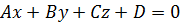- уравнение плоскости, а 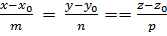- канонические уравнения прямой. Тогда формула (24) приобретает вид:

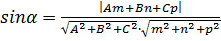(25)

Для нахождения точки их пересечения надо уравнение прямой представить в параметрическом виде, вводя параметр :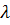

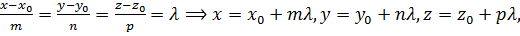(26)

Далее надо выражение (26) подставить в уравнение плоскости:

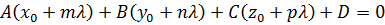, (27)

откуда находим значение параметра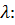

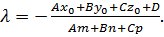(28)

Подставив найденное по формуле (28) значение 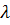в формулы (26) получим координаты точки пересечения прямой и плоскости – ведь это значение 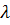удовлетворяет и уравнению прямой (см. формулу (26)) и уравнению плоскости (см. формулу (27)). Формулу (28), конечно, запоминать не надо – надо в каждой задаче решать уравнение (27). Вместе с тем, формула (28) показывает, что знаменатель не должен равняться нулю: 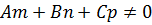. Но это ведь скалярное произведение вектора нормали плоскости 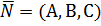и направляющего вектора прямой 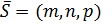, и если оно равно нулю, то векторы перпендикулярны, а прямая и плоскость параллельны. Если при этом и числитель в формуле (28) равен нулю, т.е. опорная точка прямой принадлежит плоскости, то и вся прямая лежит в плоскости.

Пример 7. Найдём координаты точки пересечения прямой 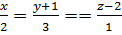и плоскости 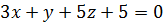и вычислим угол между ними.

Решение. Вводим параметр 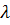и записываем параметрические уравнения прямой: 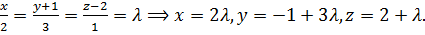Эти выражения подставляем в уравнение плоскости: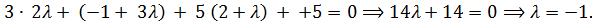

Итак, значение параметра 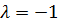соответствует точке, которая лежит в плоскости. Найдём её координаты: 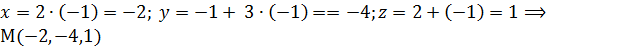- точка пересечения прямой и плоскости.

Угол между прямой и плоскостью находим по формуле (25) для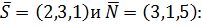

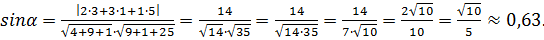
По таблицам находим .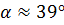

5.8. Различные уравнения прямой линии на плоскости.

у М С самого начала следует заметить,

n что на плоскости (в двумерном

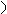
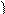
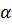0 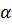х пространстве) прямую линию

Рис. 9

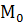m можно задавать опорной точкой

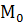и направляющим вектором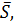

т.е. так же, как и в трёхмерном пространстве. Поэтому все рассуждения и формулы параграфа 5.5. будут сохраняться с той лишь разницей, что количество координат будет две. Поэтому соответствующие формулы можно просто переписать. Пусть 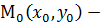опорная точка, 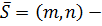направляющий вектор прямой, М (х, у) – произвольная точка прямой.

Тогда: 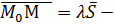векторное уравнение прямой;

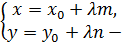(29)

параметрические уравнения прямой,

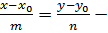(30)

каноническое уравнение прямой;

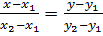- (31)

уравнение прямой, проходящей через две точки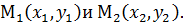

Уравнение (30) перепишем в виде 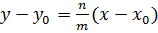и заметим (см. рис. 9), что 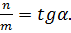Это число обозначают буквой 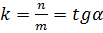и называют угловым коэффициентом прямой. Таким образом,

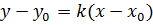- (32)

уравнение прямой с опорной точкой и угловым коэффициентом.

Если в уравнении (32) раскрыть скобки и обозначить 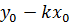буквой в: 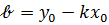, то получим

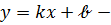(33)

уравнение прямой с угловым коэффициентом.

Кроме очевидной аналогии теории для прямой на плоскости и в пространстве можно заметить следующее весьма интересное обстоятельство. Прямая на плоскости (в отличие от прямой в пространстве) вполне определена, если известна опорная точка 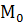и вектор нормали 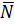, т.е. она определяется также, как плоскость в пространстве и, следовательно, на неё могут быть распространены все рассуждения и формулы параграфа 5.1. Пусть 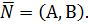Тогда (см. рис.9)

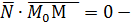(34)

векторное уравнение (наряду с уравнением (27)) прямой на плоскости,

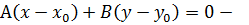(35)

уравнение прямой с опорной точкой и вектором нормали.

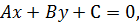(36)

где 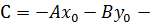общее уравнение прямой на плоскости.

Угол между двумя прямыми можно вычислять привычным для нас способом – с помощью скалярного произведения направляющих векторов прямых или их векторов нормали. Если две прямые заданы каноническими уравнениями

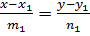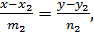и т.е. 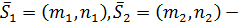направляющие векторы прямых, то (см. рис.10)

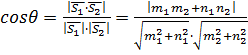(37)