Тени пересекающихся многогранников (от здания)

Тени пересекающихся многогранников (от здания)

При решении задач на построение теней пересекающихся многогранников не ограничиваются определением контуров собственных теней данных поверхностей и падающих теней от них на плоскости проекций. Задачи завершаются построением падающих теней от неосвещенных граней одного тела на пересекающиеся с ними освещенные грани второго. Каждая линия искомого контура будет представлять собой пересечение лучевой плоскости, проходящей через ребро неосвещенной грани одного многогранника, с освещенной гранью второго.

Таким образом, в основе всех построений будет решение задачи об определении тени от прямой на плоскости, где для ее решения используется метод обратных лучей. Такая задача рассматривалась на рис. 86 и 87.

На рис. 96, 97 изображены два взаимно пересекающихся многогранника (в ортогональных проекциях и аксонометрии).

Прежде всего строим контуры их падающих теней на плоскость Н, по которым определяем собственные тени. Затем нужно установить, имеют ли место случаи, когда неосвещенная грань одного тела пересекает освещенную грань другого.

При построении падающей тени от грани DCI'E' левой призмы на грань I'M'NF правой, воспользуемся обратными лучами, которые проведены через точки I' и П'.

Метод обратных лучей является весьма удобным, но не единственным при построении тени от многогранника на многогранник.

В некоторых случаях рационально использовать точки пересечения ребер с гранями, на которые падает тень от данного ребра. Эти точки не всегда могут быть в пределах контура грани.

На рисунке тень от ребра СD левой призмы на грань FNG'1' правой построена с помощью точек D_Т и III. Точка D_T(D_T',D_T'') представляет собой падающую тень от вершины D на грань FNG'1'. Тень от ребра DE' на грань FNG'1' построена при помощи точек D_T(D_T',D_T'') и IV(IV,IV''). Последняя построена в результате пересечения продолженных за пределы своих контуров граней DCI'E' и 1'FNG'.

Рис. 96

Рис. 97

Тени на фасадах зданийТени на фасадах зданий

Построение теней на фасадах зданий основано на определении точек пересечения световых лучей с вертикальными плоскостями фасада или с наклонными скатами крыши.

Определяя контур падающей тени, который является параллельной проекцией контура собственной тени, рекомендуется пользоваться следующими правилами.

1. Тень от плоской фигуры, падающая на параллельную ей плоскость, равна самой фигуре.

2. Тень отрезка прямой на параллельную ему плоскость равна и параллельна самому отрезку.

3. Если прямая перпендикулярна к плоскости, то тень прямой на этой плоскости совпадает с направлением проекции луча.

Построение теней в нишах

ПРИМЕР 1. На рис. 98, 99 в аксонометрии и в ортогональных проекциях изображена прямоугольная ниша, в которой необходимо построить собственные и падающие тени.

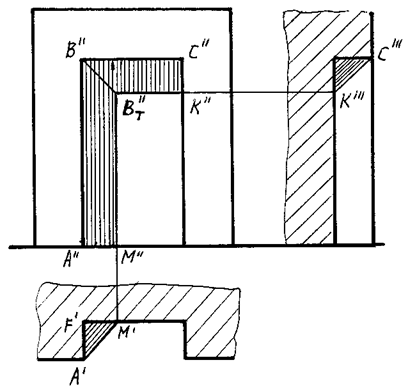
Рис. 98

Расположение граней таково, что в собственной тени находятся левая боковая и верхняя грани, поэтому собственная тень ограничена ломаной линией ABCDEFA.

Так как отрезки CD, DE, EF, FA являются внутренними ребрами ниши, то они входят одновременно и в контур падающей тени, то есть проходят по границе, отделяющей собственную тень от падающей. Строить падающую тень необходимо лишь от ребер АВ и ВС.

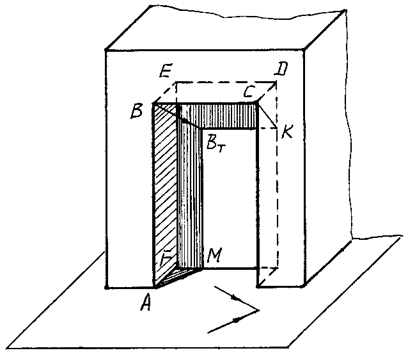
Рис. 99

ПРИМЕР 2. На рис. 100 дана ниша, перекрытая полуциркульной аркой.

Контуром собственной тени в этом примере является линия ABDEFKA, в состав которой входит образующая цилиндра DE. Последняя определяется как линия касания к цилиндрической поверхности арки касательной лучевой плоскостью Q, перпендикулярной к V.

Рис. 100

На участке DEFKA контур собственной тени одновременно является также контуром падающей тени.

Начинать построение падающей тени целесообразно с определения условной падающей тени С_T'' от центра С полуокружности G. Из полученной точки С_T'' описываем дугу окружности в пределах от точки В_T'' до точки N_T''. В точке В_T'' к этой дуге примыкает вертикальная тень В_T''А_T'' ребра АВ.

Тени от выступов

На рис. 101, 102 изображена модель части стены здания с вертикальными выступающими углами АВ и CD и с горизонтальным пояском.

Здесь в собственной тени находятся боковые грани, видимые в аксонометрии, и нижняя горизонтальная грань пояска.

Построение теней, падающих от вертикальных выступов АВ и CD на фронтальные плоскости стены, а также тени, падающей на стену от прямолинейной фронтальной части пояска, не представляет трудностей.

Несколько сложнее форма падающей тени в месте огибания пояском выступа CD. Построение падающей тени в этом месте следует расчленить на две самостоятельные задачи.

Рис. 101

Рис. 102

1. Построение тени, падающей от вертикального ребра на стену здания и на поясок (здесь повторяются построения, выполняемые при определении тени, падающей от ребра АВ).

2. Построение тени, падающей на стену и поясок от выступа (излома) пояска.

МЕТОДЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА

План:

8.1. Îáùèå ñâåäåíèÿ.

8.2. Çàìåíà ïëîñêîñòåé ïðîåêöèé.

8.3. Âðàùåíèå âîêðóã îñè, ïåðïåíäèêóëÿðíîé ïëîñêîñòè ïðîåêöèé.

8.4. Ïëîñêîïàðàëëåëüíîå äâèæåíèå.

Общие сведения

В рассмотренных задачах определялось взаимное расположение в пространстве геометрических фигур. Такие задачи называют позиционными.

В практике встречаются задачи, в которых требуется определить истинную величину, например, отрезка, угла и др. Такие задачи называют метрическими.

Для того чтобы найти истинную величину фигуры, ее располагают параллельно одной из плоскостей проекций. При этом фигуру можно перевести из общего положения в частное либо вращением самой фигуры, либо заменой положения плоскостей проекций (H и V).

Необходимо заметить, что эти способы применяют не только для определения истинных величин фигур, но и с целью упрощения решения задач.

Замена плоскостей проекций

Сущность способа замены плоскостей проекций заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей проекций новой системой взаимно перпендикулярных плоскостей проекций (рис. 103).

Рис. 103

При переходе к новой системе одну из плоскостей проекций заменяют новой таким образом, чтобы данный геометрический элемент (прямая, плоскость) занял частное положение и проецировался без искажения.

При решении ряда задач, например, требуется преобразовать прямую общего положения в прямую уровня, а затем — в проецирующую, выполнив при этом последовательно два преобразования.

Рассмотрим ход решения этой задачи.

Рис. 104

1 ПРЕОБРАЗОВАНИЕ (рис. 104,а). Для того, чтобы прямая АВ стала линией уровня, следует ввести новую плоскость проекций и расположить ее параллельно данной прямой. При этом новая ось x₁ будет параллельна одной из проекций прямой. Проведем ось параллельно горизонтальной проекции АВ. Новая плоскость проекций V₁ расположится параллельнопрямой АВ, которая проецируется на эту плоскость в истинную величину*

Правило: при замене плоскостей проекций расстояние от новой проекции точки до новой оси равно расстоянию от заменяемой проекции точки до старой оси проекций.

Иными словами, высоты (аппликаты) концов отрезка в новой системе плоскостей проекций останутся прежними. В результате этой замены решена задача на определение действительной величины отрезка и угла наклона a к плоскости H. На чертеже плоскость V₁ совмещают с плоскостью H.

2 ПРЕОБРАЗОВАНИЕ (рис. 104,á). Для того, чтобы прямая АВ оказалась проецирующей, т.е. изобразилась точкой, необходимо произвести вторую замену плоскости проекций и расположить новую плоскость H₁ перпендикулярно прямой. Новую ось x₂ располагаем перпендикулярно новой фронтальной проекции прямой А"₁В"₁. На новой плоскости проекций Н₁ прямая изобразится точкой, так как координаты концов отрезка в системе Н/V₁ одинаковы.

Таким образом, прямая АВ в системе H₁/V₁ стала проецирующей относительно плоскости H₁. Преобразования в этой задаче могли быть выполнены и в другой последовательности: сначала могла быть заменена горизонтальная плоскость проекций, а затем — фронтальная.

Рассмотрим еще одну задачу — требуется определить истинную .

величину плоской фигуры — треугольника АВС, занимающего в пространстве общее положение. Для решения этой задачи необходимо преобразовать чертеж (эпюр) так, чтобы плоскость общего положения стала параллельнойодной из плоскостей проекций новой системы*.

Сначала заменим фронтальную плоскость проекций новой плоскостью V₁, перпендикулярнойплоскости треугольника. Это условие выполнено с помощью вспомогательной прямой — линии уровня (горизонталь AN) (рис. 105). Новая ось x₁ проводится перпендикулярногоризонтальной проекции горизонтали. На новой плоскости проекций V₁ горизонталь спроецировалась в точку, а плоскость треугольника — в линию. Угол a определяет угол наклона треугольника к горизонтальной плоскости H.

Рис. 105

На втором этапе решения задачи проводим вторую замену — новую плоскость проекций H₁ устанавливаем параллельнотреугольнику. Новóю ось x₂ проводим параллельно новой фронтальной проекции треугольника — прямой b₁a₁c₁. Построенная проекция определяет истинную величину и форму треугольника.

СПОСОБ ВРАЩЕНИЯ

Сущность способа вращения также состоит в изменении положения объекта, заданного на комплексном чертеже (эпюре), таким образом, чтобы определенные его элементы заняли относительно плоскостей проекций частное положение и проецировались без искажения.

Вращение может производится вокруг осей, расположенных относительно плоскостей проекций различным образом.