Тема лекции: Потенциальная энергия упругих систем. Статические неопределимые стержневые системы
Под внешним воздействием система деформируется. При этом элементы системы перемещаются, а силы, приложенные к элементам системы, совершают работу.
Для получения наиболее общих выводов вводят понятие «обобщенная сила» и «обобщенное перемещение». Под обобщенной силой подразумевают не только сосредоточенную силу, но и любую группу сил. Каждой обобщенной силе соответствует обобщенное перемещение, и наоборот. Так, например, линейному перемещению соответствует сосредоточенная линейная сила, а угловому перемещению (углу поворота элемента) – момент.
Обобщенные силы, равно как и обобщенные перемещения, могут иметь различную размерность, но их произведение всегда имеет размерность работы.
Работа внутренних сил численно равна потенциальной энергии деформации системы, которая возвращает систему в первоначальное состояние после снятия нагрузки. Так как потенциальная энергия W положительна, то
W = – V = T (69)
Определим потенциальную энергию плоской системы, которая состоит из прямых или слегка искривленных стержней. Выделим бесконечно малый элемент dS и приложим к нему внутренние силы N, M и Q, которые по отношению к элементу будут внешними (рис.35).
|
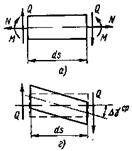
а – система внутренних сил в элементе; б, в и е – деформированные состояния элемента при растяжении, изгибе и сдвиге.
Рисунок 35 – Cхемы к определению потенциальной энергии плоской системы.
Выразим потенциальную энергию деформации элемента dS через работу внешних для него сил N, M и Q.
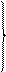 Учитывая, что на каждом перемещении (абсолютной деформации) работу производят только соответствующие силы (рис.35, б, в и г), получим основе известных формул сопротивления материалов:
Учитывая, что на каждом перемещении (абсолютной деформации) работу производят только соответствующие силы (рис.35, б, в и г), получим основе известных формул сопротивления материалов:
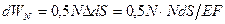 ;
;
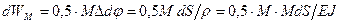 ; (70)
; (70)
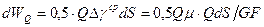 .
.
где 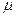 – коэффициент, учитывающий закон распределения касательных напряжений и зависящий от формы поперечного сечения: для прямоугольников
– коэффициент, учитывающий закон распределения касательных напряжений и зависящий от формы поперечного сечения: для прямоугольников 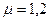 , для прокатных профилей
, для прокатных профилей 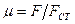 (F – полная площадь сечения ,
(F – полная площадь сечения , 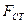 – площадь вертикальной стенки).
– площадь вертикальной стенки).
Выражение полной потенциальной энергии плоской системы получим путем интегрирования и суммирования выражений (70),т.е.
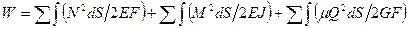 (71)
(71)
Для пространственной стержневой системы, состоящей из прямолинейных стержней, формула потенциальной энергии имеет следующий вид:
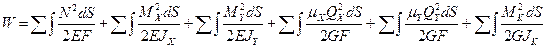 , (72)
, (72)
где первый член учитывает деформации растяжения, второй и третий – деформации изгиба в разных плоскостях, четвертый и пятый - деформации сдвига в разных плоскостях, а последний –деформации кручения.
Из формул (71) и (72) следует, что:
– потенциальная энергия W всегда положительна, так как выражения внутренних сил берутся в квадрате;
– на потенциальную энергию не распространяется принцип независимости действия сил ( 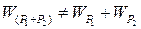 ),поскольку потенциальная энергия является не линейной, а квадратичной функцией усилий;
),поскольку потенциальная энергия является не линейной, а квадратичной функцией усилий;
– величина потенциальной энергии не зависит от последовательности загружения, а лишь от начального и конечного состояния упругой системы.