Взвешенный критерий произведений.

Критерий произведений не учитывает тенденцию в изменении выплат, поэтому для ситуаций, в которых важную роль играет фактор времени, чаще используют модификацию этого критерия, так называемый взвешенный критерий произведений[7].

1. Решающая функция: взвешенное произведение выплат по i-ой строке таблицы выплат:

.

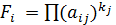2. Решающее правило: .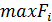

По этому критерию оптимальным является решение, которому соответствует наибольшее взвешенное (с весами 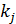) произведение возможных выплат. Веса 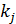определяются в зависимости от специфики ситуации: если ситуация развивается во времени, то обычно придается большее значение событиям недавним и меньшее значение событиям в далеком прошлом.

Один из способов выбора таких весов дает модель Брауна[8].

1. Выбирается параметр 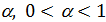. Способ выбора 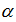зависит от конкретной задачи, но если нет дополнительных условий, то можно использовать правило:

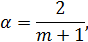
где m – число моментов времени.

2. Моментам времени 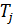присваиваются веса в соответствии с таблицей.

Момент времени,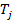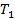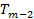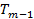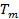
Вес,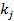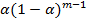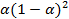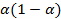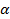

Пример 4.2.

Известны доходности (в %) по трем активам за четыре месяца.

Актив	Месяц
Сентябрь	Октябрь	Ноябрь	Декабрь

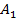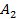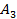Выбрать один актив для инвестирования.

Решение.

1. Используем критерий произведений. Для этого по каждому варианту решения определим произведение выплат :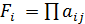

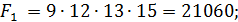
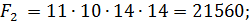
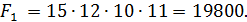
Согласно решающему правилу максимальное произведение выплат 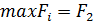, т.е. оптимальным является выбор актива .

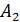2. Рассмотрим взвешенный критерий произведений. Для этого определим параметр 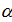по формуле:

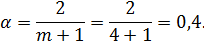
Определим веса 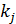для каждого месяца.

Месяц	Сентябрь	Октябрь	Ноябрь	Декабрь
Вес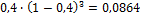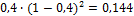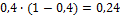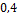

Далее по каждому варианту решения определим взвешенное произведение выплат :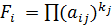

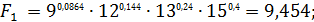
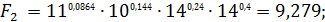
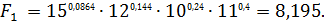
Согласно решающему правилу максимальное взвешенное произведение выплат 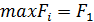, т.е. оптимальным является выбор актива .

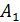Следует отметить, что критерий произведений указал на актив 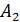как на более стабильный, т.е. по этому активу можно предполагать относительно стабильную доходность (без резких «скачков»). Взвешенный критерий произведений оптимальным считает актив 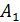, поскольку этот актив имеет положительный тренд, т.е. здесь можно ожидать дальнейшего роста доходности.

ТЕМА 5. ПРИНЯТИЕ РЕШЕНИЙ В СИТУАЦИЯХ КОНФЛИКТА

И КОНКУРЕНТНОЙ БОРЬБЫ

На практике часто приходится сталкиваться с задачами, в которых необходимо принимать решения в ситуациях, в которых две стороны преследуют различные цели, и результаты действия каждой из сторон зависят от мероприятий противника (или партнера).

Ситуация конфликта– ситуация, в которой решение принимается с учетом противодействия разумного информированного противника; не является нейтральной средой, т.е. состояние среды (заранее неизвестное) зависит от того, какой вариант решения выбирает игрок.

Конфликт – это борьба сторон с противоположными интересами. В ходе конфликта каждая из сторон стремится нанести ущерб другой стороне и минимизировать собственные потери.

Конфликт всегда связан с определенного рода разногласиями (это не обязательно антагонистическое противоречие). Конфликтная ситуация называется антагонистической, если увеличение выигрыша одной из сторон на некоторую величину приводит к уменьшению выигрыша другой стороны на такую же величину, и наоборот.

В экономике конфликтные ситуации встречаются очень часто и имеют многообразный характер. Например, взаимоотношения между поставщиком и потребителем, покупателем и продавцом, банком и клиентом. Каждый из них имеет свои интересы и стремится принимать оптимальные решения, помогающие достигнуть поставленных целей в наибольшей степени. При этом каждому приходится считаться не только со своими целями, но и с целями партнера и учитывать решения, которые эти партнеры будут принимать (они заранее могут быть неизвестны).

Чтобы в конфликтных ситуациях принимать оптимальные решения, создана математическая теория конфликтных ситуаций, которая называется теорией игр.

Игра – это математическая модель реальной конфликтной ситуации. Стороны, участвующие в конфликте, называются игроками. Исход конфликта называется выигрышем. Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков больше двух. Будем рассматривать только парные игры. Игроки обозначаются A и B.

Игра называется антагонистической (с нулевой суммой), если выигрыш одного из игроков равен проигрышу другого. В такой игре общая сумма вовлеченных в нее активов в ходе игры не меняется.

Цель теории игр – разработать методы для определения оптимальной стратегии каждого игрока. Стратегия игрока называется оптимальной, если она обеспечивает этому игроку при многократном повторении игры максимально возможный средний выигрыш (или минимально возможный средний проигрыш независимо от поведения противника).

Ситуацию неопределенности можно рассматривать тоже как конфликт, но с одним существенным отличием: при настоящем конфликте имеем дело с противником, который способен предугадать наши шаги и принять меры для снижения своих потерь; а в ситуации неопределенности – с противником, именуемым «природа», который действует «слепо» и не способен на осознанные ответы.

Антагонистическая парная игра представляется в виде матрицы или таблицы выплат A, в которой ходы (стратегии) игрока A расположены по строкам, а ходы (стратегии) игрока B расположены по столбцам (табл.5.1).

Таблица 5.1

Общий вид таблицы выплат в парной конкурентной игре

Вариант решения игрока A	Вариант ответа игрока B
B1	B2	…..	Bm
А1	a11	a12		a1m
А2	a21
…..
Аn	an1			anm

В самой матрице (таблице) записаны выигрыши игрока A при соответствующих ходах игроков A и B (отрицательный выигрыш – это проигрыш). Т.е. 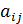– платеж второго игрока первому (выигрыш игрока A), тогда выигрышем игрока B будет ( 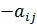). Если 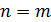, то игра называется симметричной.

Чтобы решить игру, заданную такой таблицей, необходимо найти верхнюю и нижнюю цены игры и определить, имеет ли данная игра седловую точку (нижняя цена игры должна быть равна верхней цене игры).

Простота решения игры с седловой точкой заключается в том, что оптимальные стратегии обоих игроков находятся сразу. Такое решение обаладет свойством устойчивости – если один из игроков применяет свою оптимальную стратегию, то любое отклонение другого игрока от оптимальной стратегии может оказаться невыгодным для него.

Рассмотрим поэтапно формирование оптимальных стратегий двух игроков.

Оптимальная стратегия игрока 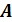. Нижняя цена игры.

Выбирая стратегию 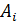, необходимо рассчитывать, что игрок B ответит на нее такой стратегией 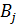, для которой выигрыш игрока A будет минимальным. Чтобы определить такую стратегию игрока A, необходимо выполнить следующие действия.

1. Для каждой стратегии игрока A определяем минимальное значение выплаты по i-ой строке таблицы выплат:

.

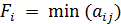2. Среди этих минимумов определяем максимальное значение: .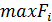

Обозначим 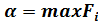- гарантированный выигрыш, который может обеспечить себе игрок A. Этот выигрыш называется нижней ценой игры или максимином.

Стратегия 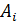, обеспечивающая получение нижней цены игры, называется максиминной (перестраховочной). Если игрок A будет придерживаться этой стратегии, то ему гарантирован выигрыш, равный или превышающий величину 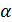, при любом поведении игрока B.

Оптимальная стратегия игрока 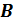. Верхняя цена игры.

Игрок B заинтересован в уменьшении выигрыша A. Выбирая стратегию 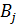, он, из соображений осторожности, учитывает максимально возможные при этом выигрыши A. Чтобы уменьшить выигрыш A, из этих максимально возможных выигрышей игрок B выбирает наименьший. Определим такую стратегию игрока B, выполнив следующие действия.

1. Для каждой стратегии игрока A определяем максимальное значение выплаты по j-ому столбцу таблицы выплат:

.

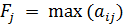2. Среди этих максимумов определяем минимальное значение: .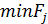

Обозначим y m:val="bi"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:b/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:vertAlign w:val="subscript"/><w:lang w:val="EN-US"/></w:rPr><m:t>j</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 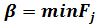- гарантированный проигрыш игрока B, т.е. он проиграет не больше, чем 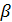. Этот проигрыш называется верхней ценой игры или минимаксом. Стратегия игрока B, обеспечивающая выигрыш, равный или превышающий величину 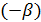, называется его минимакснойстратегией.

Седловая точка.

Если 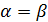, т.е. минимакс совпадает с максимином, то такая игра называется игрой с седловой точкой. Седловая точка – это пара оптимальных стратегий .

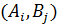В этом случае число 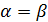называется (чистой) ценой игры (нижняя и верхняя цена игры совпадают). Это означает, что матрица содержит такой элемент, который является минимальным в своей строке и одновременно максимальным в своем столбце.

Если седловая точка существует, то оптимальными стратегиями игроков, являющимися решением игры, будут их чистые стратегии, соответствующие седловой точке. Цена игры равна верхней и нижней цены игры, которые равны между собой. Если игра не имеет седловой точки, то решение игры следует искать в смешанных стратегиях.

Оптимальные стратегии в любой игре обладают важным свойством, а именно – устойчивостью. Это означает, что каждый из игроков не заинтересован в отходе от своей оптимальной стратегии, т.к. это ему невыгодно. Отклонение от оптимальной стратегии игрока А приводит к уменьшению его выигрыша, а одностороннее отклонение игрока В – к увеличению проигрыша. Если в игре есть седловая точка, то в ней существует положение равновесия.

Пример 5.1.

Фирма А рассматривает меры по снижению потерь от усилившейся конкуренции фирмы В. Этими мерами могут быть: улучшение качества ранее производимой продукции; выпуск нового вида продукции. Конкурирующая фирма может ответить тем же самым.

Ожидаемые изменения выплат для фирмы А в зависимости от ответов фирмы В представлены в таблице, приведенной ниже (в млн. у.е.).

Выбор фирмы А	Возможные ответы фирмы В
Ничего не делать	Повысить качество	Выпустить новую продукцию
Ничего не делать	-10	-15	-20
Повысить качество		-5	-10
Выпустить новую продукцию	+10		-5

Определить оптимальные стратегии фирмы A и B.

Решение.

Найдем верхнюю и нижнюю цены игры, определив минимумы и максимумы выплат по строкам и столбцам соответственно (в таблице выплат достроим столбец минимумов и строку максимумов).

Выбор фирмы А	Возможные ответы фирмы В	Минимальный выигрыш,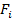
Ничего не делать	Повысить качество	Выпустить новую продукцию
Ничего не делать	-10	-15	-20	-20
Повысить качество		-5	-10	-10
Выпустить новую продукцию			-5	-5
Максимальный выигрыш,	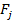		-5	-5 (цена игры)

Нижняя цена игры составила 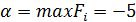; верхняя цена игры составила 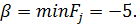Т.е. фирма А потеряет не более 5 млн. у.е., а фирма B выиграет не менее 5 млн. у.е.

Т.к. 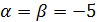, т.е. минимакс совпадает с максимином, то такая игра называется игрой с седловой точкой. Цена игры здесь составила 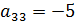. В этой игре существует положение равновесия.

Замечание. Если цена игры оказывается равной нулю, тогда игра называется безобидной. В данном примере игра безобидной не является.

Оптимальное решение в игре с седловой точкой определим с помощью максимина, т.е. по максимуму в столбце минимумов. Таким образом, оптимальным решением для фирмы A является «выпуск новой продукции».