Екі дененін мәселесі. Кеплер заңдарының дәл түрі

Бүкіл әлемдік тартылыс заңынан Кеплердің заңдарын қорытуға болады. Бұл жағдайда тек екі дене ғана – Күн және планета – қарастырылады, өйткені, Күннің әсеріне салыстырғанда басқаларының әсері өте аз. Сондықтан қарастырылатын есеп «екі дененің мәселесі» деп аталады.

Айталық, Күннің массасы М, ал оның айналасындағы қозғалатын планетаның массасы . Қозғалмайтың жүйенің бастапқы нүктесі ретінде Күннің массалық «С» центрің алып, Р планетаның күннің гравитациялық өрісінде қозғалыс заңдылықтарын анықтайық (7-сурет). Р планетаның салыстырмалы үдеуі

Егерде (1) деп белгілейтін болсақ,

Бұл үдеудің координат осьтеріне проекцияларын мына теңдеулерден табуға болады.

7-сурет. Күн С және планета Р

бағыттаушы косинустар деп аталып, олар тең болады.

Соңда Р планетаның салыстырмалы қозғалысының дифференциалды теңдеулері:

(2) системаның жалпы шешулерін іздестірейік. Олар интегралдар деп аталады. Ол үшін (2) системаның 3 теңдеуін у-ке, ал 2-ші теңдеуін -ке көбейтіп, 3-деп 2-ні алып тастайық:

Дәл осылай тағы екі теңдеуді шығарамыз:

Осы үш теңдеуді интегралдайық, сонда

Бұл үш теңдеу Р планетаның С Күннің гравитациялық өрісіндегі қозғалысының бірінші интегралы – аудандық интеграл, ал С₁, С₂, С₃ – тұрақтылар.

(3) мистеманың І-ші теңдеуін х-ке, 2-сін, у-ке, ал 3-сін -ке көбейтіп қоссақ:

(4)

Бұл жазықтықтың теңдеуі. Сөйтіп планетаның орбитасы жазық қисық екен, және ол орбита жазықтығы Күннің массалық центрі арқылы өтеді.

Енді Сху жазықтықты орбита жазықтығы деп есептейік, сонда . Осылай болса (3) системаның үшінші теңдеуі қалады:

(5)

х, у координаталарды полярлық координаттарға алмастырып жазсақ, онда:

Осы өрнектерді (5) теңдеуге өндірсек мына қатынас алынады:

(6)

Планетаның радиус-векторының сызатын секторлық ауданының дифференциалы немесе (6) теңдеуден . Осы теңдеуді интегралдасақ , немесе – екі еселенген секторлық жылдамдық болатынын көреміз. Сондықтан (6) теңдеуді сөзбен былайша айтуымызға болады:

Планетаның радиус-векторы тең уақыт аралығында тең аудандар сызады.

Демек, бұл Кеплердің ІІ заңы.

Енді планетаның орбитасының формасын анықтайық. Сху орбитаның жазықтығы болатын болса, (2) системаның 3-ші теңдеуі жойылып, 2 теңдеу қалады:

Бұл теңдеулердің 1-шісін , ал ІІ-сін көбейтіп қоссақ:

(7)

Мұның сол жағын былай жазуға болады:

планетаның жылдамдығы. Оң жағын түрлендіру үшін радиус-вектор 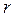-дің х, у координаттарымен өрнектейтін теңдеуді аламыз:

Осы теңдеуден туынды алсақ:

, сондықтан (7) теңдеуді былай жазамыз:

Осы теңдеуді интегралдаймыз, сонда

, (8)

С – тұрақты және (8) интеграл «тірі күштер интегралы» немесе «энергия интегралы» деп аталады. Осы интегралдан радиус – вектор 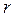-дың өрнегін шығарып, планетаның орбитасының формасын табамыз.

(8) интегралдағы v жылдамдықты поляр координатта жазайық, соңда:

(6) теңдеу бойынша ,

ал

Сонда жазылуы:

Енді айнымалыға көшеміз, ал . Сондықтан:

айнымалыны мына формуламен өрнектесек:

Соңғы теңдеудің мынаған айналатыны түсінікті:

, немесе

, яғни .

Егерде десек , осыдан , немесе таңбасын алған ыңғайлы. Сонда: ; осыны интегралдасақ: , тұрақты. Осыдан , ал

Сонда, – параметр, -шын аномалия. немесе

(9)

(9) теңдеуі конус қимасының теңдеуі /эллипс, парабола, гипербола/.

Сондықтан бұл нәтижені былай айтуға болады:

Тартылыс күштің әсерінен аспан денесі екінші дененің гравитациялық өрісінде конус қимасы /эллипс, парабола, гипербола/ бойынша қозғалады.

Бұл Кеплердің жалпы І заңы. Осы түрінде бұл заң барлық аспан денерінің қозғалысын дұрыс көрсетеді. Басқаша айтқанда, кометалардың, планеталардың серіктерінің, физикалық қос жұлдыздардың, жасанды денелердің т.б. гравитациялық өрістеріндегі қозғалысының орбиталарының формасын анықтайды.

Орбитаның формасы тек бастапқы жылдамдығына байланысты екенін көрсетейтік. Шынында да,

1) Эллипс, ;

2) Парабола, ;

3) Гипербола, .

Енді Кеплердің ІІІ заңын қорытып шығарамыз. Аудандық интегралдың С₃ –тұрақтысы екі еселенген секторлық жылдамдық.

Демек,

Сонда,

Орбитаның параметрі , сондықтан , ал

Сонда,

, немесе

(10)

тұрақты.

Бұл теңдеу Кеплердің ІІІ заңының математикалық түрі. Екі планета үшін (10) мынадай түрде жазылады:

Кеплердің ІІІ заңы былай айтылады:

Планеталардың сидерлық айналыс периодтарының квадраттарының планета мен Күннің массаларының қосындысына көбейтінділері олардың орбиталарының үлкен жарты өсінің кубтеріне тура пропорционал.

Планеталардың массалары Күннің массасына салыстырғанда өте аз болғандықтан,

– Кеплердің эмпирикалық ІІІ заның осы түрдегі өрнегі алынады.

Кеплердің ІІІ заңының дәл түрін тек Күн жүйесіне емес, кез келген жүйеге қолдануға болады. Сонда (10) теңдеуде М – центрлік /орталық/ дененің массасы, ал 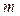-қозғалатын дененің массасы. Мұнымен қатар (10) өрнекті планета мен олардың серіктеріне және қос жұлдыздарға да қолдануға болады.